„Genetische Algorithmen sind Optimierungsverfahren, welche Optimierungsprobleme lösen“ (Harbich, 2007, S. 3). Ziel ist es, eine exakte, nicht unbedingt die optimale, Lösung in einem angemessen Zeitrahmen zu finden, die von anderen Methoden nicht gefunden werden kann. So ist zum Beispiel das Problem des Handlungsreisenden formal lösbar, indem alle Möglichkeiten überprüft werden. Dies ist aber aufgrund der Komplexitätsklasse von O(n!) nicht auf größere Probleme anwendbar, da schon bei n=30 2,6*10^32 Möglichkeiten entstehen. Genetische Algorithmen sind in der Lage diese Problemklasse effizient zu lösen. Sie sind an die biologische Evolution angelehnt und verwenden die Terminologie (vgl. Harbich, 2007, S. 3). In der Evolution sind die Chromosomen die Träger der Erbsubstanz. Einzelne Abschnitte dieser Chromosome werden als Gene bezeichnet und können verschiedene Ausprägungen (Allele) haben. Evolution bezeichnet nun die Veränderung der Gene einer Population von einer Generation zu der nächsten. Hierbei sind drei wichtige Mechanismen zu beachten:

• Selektion: Die am Besten angepassten Individuuen einer Population haben die größte Überlebenswahrscheinlichkeit und bilden somit mit einer höheren Wahrscheinlichkeit die nächste Generation. Wie stark ein Individuum angepasst ist, wird mit der Fitness beschrieben.
• Mutationen verändern willkürlich einzelne Allele von Genen.
• Crossover: Hierbei werden mehrere Allele zusammen von einem Chromosom zum nächsten ausgetauscht

(vgl. Harbich, 2007, S. 4f).

In den nachfolgenden Kapiteln wird der genetische Algorithmus kurz erläutert und seine Umsetzung in Matlab aufgezeigt und wo nötig kommentiert. Der Code baut auf der Entwicklung von Stefan Tretner auf.

Gegeben: Optimierungsproblem mit Suchraum S und Fitnessfunktion f

Lösung:
   Generiere zufällige Startpopulation P
   SOLANGE(Abbruchbedingung nicht erfüllt)
   {
      Berechne Fitness der Individuen aus P
      Selektiere nach Fitness
      Wende genetische Operatoren an
   }
   
Ergebnis: bestes Individuum aus der Population

(vgl. Harbich, 2007, S. 5)

Als Startpopulation werden zufällige Chromosome erzeugt. Dies verhindert, dass durch eine Vorauswahl von geeigneten Chromosomen nur ein lokales Optimum gefunden wird (vorzeitige Konvergenz) (vgl. Harbich, 2007, S. 6).

Umsetzung in Matlab

% Variablen
pop_size = 50;		% Populationsgröße
generations = 100;		% Anzahl an Generationen
% Protokoll [Chromosom #, Generation #, (Chromosomausprägung, Fitnesswert)]
protocol=zeros(pop_size,generations, 2);

In dem Protokoll wird die Chromosomen- und Generationsnummer in einem Array gespeichert. Zu dieser eindeutigen Kombination (z.B. 5. Generation und 10. Chrosomom) wird die aktuelle Chromosomausprägung und der dazugehörige Fitnesswert gespeichert.

Die Fitness beschreibt die Überlebenswahrscheinlichkeit eines Chromosoms mit der Formel:
`p(c_i) = f(c_i) / (\sum_{j=1}^nf(c_j))`

Die Summe aller Überlebenswahrscheinlichkeiten ist 1 (vgl. Harbich, 2007, S. 6).

Der Fitnesswert ist abhängig von der jeweiligen Modellierung und wird in dort beschrieben.

Der nachfolgende Matlab-Code zeigt speichert das beste Chromosom in einer Variable, sodass der genetische Algorithmus zu jedem Zeitpunkt beendet werden kann und dennoch eine gültige und (zu diesem Zeitpunkt) beste Lösung vorhanden ist.

Umsetzung in Matlab

% Index von bestem Chromosom
% bestind == [fitness generation element]
bestind = [0 0 0];
 
% Prüfe, ob neues bestes Ergebnis
        if (fitness > bestind(1))
            bestind(1) = fitness;
            bestind(2) = f;
            bestind(3) = chrom;
            bestOrder = currentChrom;
            fprintf('Neues bestes Chromosom gefunden: Zykluszeit: %f ', 1-bestind(1));
            fprintf('Generation: %i ', bestind(2));
            fprintf('Chromosom: %i \n', bestind(3));
        end

Die Auswahl der Chromosomen, die die nächste Generation bilden, erfolgt aufgrund der Überlebenswahrscheinlichkeit. Alle Überlebenswahrscheinlichkeiten werden in ein Intervall gespeichert. Eine Pseudozufallszahl wählt nun ein Chromosom aus. Es ist sofort ersichtlich, dass Chromosomen mit einer größeren Überlebenswahrscheinlichkeit öfter ausgewählt werden. Dieser Vorgang wird so oft wiederholt, bis die nachfolgende Generation die gleiche Populationsgröße wie die vorherige hat.

Abb. x: Selektion der Chromosomen anhand ihrer Überlebenswahrscheinlichkeit (Harbich, 2007, S. 7)

Umsetzung in Matlab

% Sortiere aktuelle Population nach Fitness
    protocol(:,:,f) = sortrows(protocol(:,:,f),2);
 
    % Erstelle neues Intervall [0,1]
    R = rwheel(protocol(:,:,f),2);
 
    % Erstelle temporäre Generation
    Pnew = zeros(pop_size,64);
 
    % Fülle temporäre Generation mit alten Chromosomen anhand deren Wahrscheinlichkeit
    for i=1:1:length(P(:,1))
        Pnew(i,:) = P(wheel_select(protocol(:,:,f),R),:);
    end
 
    % Kopiere Pnew nach P
    P = Pnew;
 

% Erstellt [0,1] Intervall mit Wahrscheinlichkeit für alle Chromosome
function R = rwheel(pop,row)
    R = zeros(length(pop),1,'double');
    summe = sum(pop(:,row));
        for id = 1:1:length(pop)
            R(id) = sum(pop(id:end,row))/summe;
        end
end

% Gibt Chromosom in Abhängigkeit von Zufallszahl zurück
function partner = wheel_select(pop,thewheel)
    rnd = rand(1);
    id = length(thewheel);
    while id > 1 && rnd > thewheel(id) 
        id = id-1;
    end
    partner = pop(id,1);
end

Die Chromosome der nachfolgenden Generation werden nun mutiert bzw. ausgetauscht (crossover) (vgl. Harbich, 2007, S. 7).

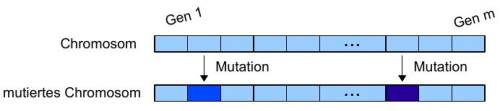
Bei der Mutation werden zufällig die Gene eines Chromosoms verändert. Hierbei wird die Wahrscheinlichkeit meist auf 1/Anzahl der Gene gesetzt. Ist ein Gen ausgewählt worden, so wird dieses durch ein zufälliges, aber existierendes Allel ersetzt. Somit ist gewährleistet, dass mit dem veränderten Chromosom gerechnet werden kann (vgl. Harbich, 2007, S. 7f).

Abb. x: Mutation eines Chromosoms (Harbich, 2007, S.8)

Umsetzung in Matlab

% Schleife über alle Chromosome
    for i=1:1:pop_size
        for gen = 1:1:64
	% Wenn ausgewählt
            if rand(1) <= p_mut
                % Neue Zahl finden, die anders ist als bestehende
                random = randi(9)-1;
                while P(i,gen) == random
                    random = randi(9)-1;
                end
                P(i,gen) = random;
                mutcount = mutcount + 1;
            end
        end
    end
 

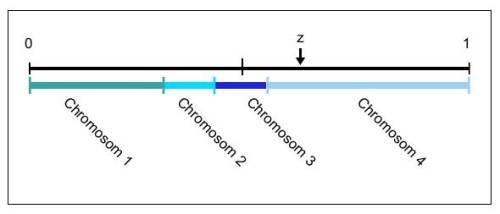
Bei der Kreuzung werden immer zwei Chromosome paarweise ausgewählt. Über eine Zufallszahl wird entschieden, ab welchem Segment die Allele (Zeichenkette oder Zahlen) getauscht werden sollen. Dieser Vorgang wird durch eine Wahrscheinlichkeit gesteuert (z. B. : p=0.25).

Abb. x: Crossover zweier Chromosome (Harbich, 2007, S. 8)

In der Abbildung ist das Vorgehen schematisch für zwei Chromosome gezeigt. Die Kreuzung erfolgt bei z=3 (vgl. Harbich, 2007, S. 7f).

Umsetzung in Matlab

% CROSSOVER
    % speichert Crossover-Kandidaten
    Q = [];
    for i=1:1:pop_size
        if rand(1) <= p_cross
             Q = [Q i];
        end
    end
 
    disp(['Kreuzungen: ',num2str(floor(length(Q)/2))]);
 
    % Führe Kreuzung durch
    while length(Q)>1
	% wähle erstes Element (Index) aus und lösche es aus Q
        rand1 = floor(1 + (length(Q))*rand(1));
        elem1 = Q(rand1);
        Q(rand1) = [];
 
	% wähle zweites Element (Index) aus und lösche es aus Q
        rand2 = floor(1 + (length(Q))*rand(1));
        elem2 = Q(rand2);
        Q(rand2) = [];
 
 
        father = P(elem1,:);
        mother = P(elem2,:);
        cut = floor(1 + (64-1)*rand(1));
 
        % overwrite mother & father with children
        P(elem1,1:cut) = father(1:cut);
        P(elem1,cut+1:end)= mother(cut+1:end);
 
        P(elem2,1:cut) = mother(1:cut);
        P(elem2,cut+1:end) = father(cut+1:end);
    end
 

Mit jeder neuen Generation ist es prinzipiell möglich, dass eine neue, bessere Lösung gefunden werden kann. Daher sollten andere Abbruchbedingungen definiert werden. Möglich sind:

• Abbrechen nach n Generationen
• Keine signifikante Verbesserung zur vorherigen Generation

(vgl. Harbich, 2007, S. 8)

Genetischer Algorithmus

Ordnet Chromosome in Intervall [0,1]

Wählt Chromosom auf Intervall aus

Harbich, S. 2007. Einführung genetischer Algorithmen mit Anwendungsbeispiel. Zugriff am 15. Juli 2013 unter http://www-e.uni-magdeburg.de/harbich/download.php?f=genetische_algorithmen/genetische_algorithmen.pdf

indexmenu_n_2