Inhaltsverzeichnis
2014 Christian Schumacher
| Title | Influence of mechanical and leg muscle properties on long jump performance |
|---|---|
| Titel | Einfluss der Muskeleigenschaften auf die optimale Beinfunktion für den Weitsprung |
| Supervisor | Prof. Dr.-Ing. Stephan Rinderknecht, Prof. Dr. phil. Andre Seyfarth |
| Autor | Christian Schumacher (schumach@sport.tu-darmstadt.de) |
| Department | FB 16 Mechanical Engineering |
| Last Revision | 21. November 2014 |
| Status | Finalized |
Introduction / Motivation
Der Weitsprung stellt eine sehr komplexe Bewegungsaufgabe dar, bei der die Zielgröße bzw. das Leistungsmaß durch die erreichte Sprungweite eindeutig bestimmbar ist. Der Weitsprung unterteilt sich in drei Phasen: den Anlauf, den Absprung und die Flug- bzw. Landungsphase. Grundsätzlich stellt der Weitsprung eine Umsetzung der im Anlauf erzeugten horizontalen Anlaufgeschwindigkeit in einen Teil an vertikaler und einen Teil an horizontaler Absprunggeschwindigkeit dar. Hierbei wird eine optimale Umsetzung, also ein optimales Verhältnis der Absprunggeschwindigkeiten sowie einen geringen Geschwindigkeitsverlust während des Absprungs angestrebt, um eine große Sprungweite zu erreichen.
Viele Untersuchungen in der Literatur befassen sich mit der Technikanalyse des Bewegungsmusters und stellen Korrelationen zwischen verschiedenen kinematischen Parametern und der Sprungweite auf (Hay, 1986; Nolan und Lees, 2000; Bridgett und Linthorne, 2006; Linthorne, 2010). Weitere Untersuchungen berichten davon, dass bei Sprungbewegungen aufgrund des Dehnungs-Verkürzungs-Zyklus´ (DVZ) eine erhöhte Leistungsausbeute erreicht werden kann (Nagano et al., 2004; Van Leeuwen, 1992). Dabei wird ein Teil der Energie, die bei der extensiven Belastung des Muskels (Bremsen) abgebaut wird, in den elastischen Elementen, den Sehnen, gespeichert (siehe hierzu Was ist der DVZ?). Aktuelle Forschungsergebnisse lege nahe, dass hierbei auch das Titin beteiligt ist (Titin; Rode et al., 2009).
Eine Veränderung der seriellen Steifigkeiten, und damit vermutlich auch der Sprungfähigkeit, lässt sich durch Training (Rabita et al., 2008), entsprechende rekuperierende Schuhe oder im Bereich des Behindertensports durch die Wahl einer entsprechenden Carbonfeder erreichen. Eine Untersuchung der Auswirkungen von verschiedenen seriellen Steifigkeiten auf das Arbeitsvermögen des biologischen Muskels und dessen Anteil zur Energieeinbringung im Weitsprung hat zum jetzigen Stand nicht stattgefunden.
Goal of the thesis
Ein Ziel der Arbeit ist es, die Arbeitsweise des Muskels für verschiedene Steifigkeiten der seriellen Elemente zu untersuchen. Hierbei wird die Interaktion eines kontraktilen Elements (CE) mit einem seriell elastischen Elements (SEE) untersucht. Daraus wird folgende Forschungsfrage abgeleitet:
Wie ändern die Eigenschaften des seriellen elastischen Elements (SEE) die Beinfunktion (im speziellen die Muskelfunktion)?
Approach / Methodology
Die thematisierte Zielstellung soll mit Hilfe eines Simulationsmodells untersucht werden. Dafür wird ein Feder-Masse-Modell (z.B. Seyfarth et al., 1999) mit einem vereinfachten Muskelmodell (z.B. Häufle et al., 2010) kombiniert. Diese Modellkonfiguration ermöglicht es, die Interaktion zwischen dem vereinfachten Muskel und dem seriell elastischen Element zu untersuchen. Um die Aussagekraft des Modells nicht zu vermindern und die Parameteridentifikation des Modells zu vereinfachen, wird ein möglichst simples Modell angestrebt. Dafür werden verschiedene Annahmen und Vereinfachungen getroffen, die teilweise auf Vorarbeiten basieren (Geyer et al., 2003; Häufle et al., 2010; Häufle et al., 2012). Zusätzlich werden verschiedene neuromuskuläre Anpassungsmechanismen in dem Modell implementiert und untersucht. Ein Überblick über die Methodik ist in Abbildung 2 dargestellt. Da es sich hierbei um einen iterativen Prozess handelt, wird für die Modellbildung ein Kreislauf verwendet. Die Parameteridentifikation des Modells und der Vergleich der Simulationsergebnisse mit der Realität erfolgt auf Basis von experimentellen Daten. Die Experimente werden in Zusammenarbeit mit dem Olympiastützpunkt Hessen im Landessportbund Hessen e.V. ( OSP Hessen) durchgeführt.
Results
An dieser Stelle werden lediglich die wichtigsten Ergebnisse dieser Abschlussarbeit zusammengefasst. Dabei wird zunächst auf die Modellstruktur und auf die damit erzeugte Modellqualität eingegangen, bevor die Beteiligung der verwendeten Elemente am Weitsprung beschrieben wird.
Modellstruktur
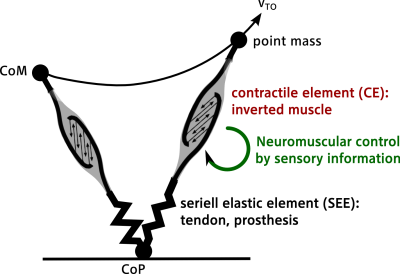
Zur Modellierung eines Simulationsmodell werden Vereinfachung aufgrund von Annahmen notwendig. Dabei wird die komplexe Struktur des menschlichen Beins auf einzelne, beim Absprung beteiligte Elemente reduziert (vgl. Abbildung 3). Diese Elemente umfassen die Komprimierung aller beteiligten Strukturen im menschlichen Körper, die an der Absprungbewegung beteiligt sind, auf eine Punktmasse, einen Muskel und ein elastisches Element. Dadurch erfolgt die Beschreibung der Dynamik des gesamten Körpers durch die Beinfunktion, die die Interaktion zwischen Körperschwerpunkt (CoM) und dem Druckmittelpunkt (CoP) entlang der Beinachse beschreibt.
Im Rahmen der Modellierung wird die in Abbildung 4 dargestellte Modellstruktur für die Untersuchung des Absprungs beim Weitsprungs entwickelt. Dabei sind ein invertiertes Muskelelement (CE) nach Häufle et al. (2010) und ein elastisches Element (SEE) seriell angeordnet. Das invertierte Muskelelement bildet die geometrische Transformation des segmentierten Beins nach. Demnach werden die Muskelfasern gedehnt, wenn die Beinlänge verkürzt wird (entspricht der Dehnung der Beinstreckermuskulatur bei der Knieflexion). Das implementierte neuromuskuläre Modell nach Geyer et al. (2003) verwendet sensorische Signale des Muskelelements, wie die Kraft, die Länge oder die Geschwindigkeit des Muskelelements.
Bei der hier verwendeten Konfiguration der Strukturelemente (CE und SEE) ergeben sich beim Bodenkontakt folgende Zusammenhänge für die Längeänderung und die Kraft des Gesamtbeines:
| $\Delta l_{Bein} = \Delta l_{CE} + \Delta l_{SEE} $ $ F_{Bein} = F_{CE} = F_{SEE} $ |
Simulationsergebnisse
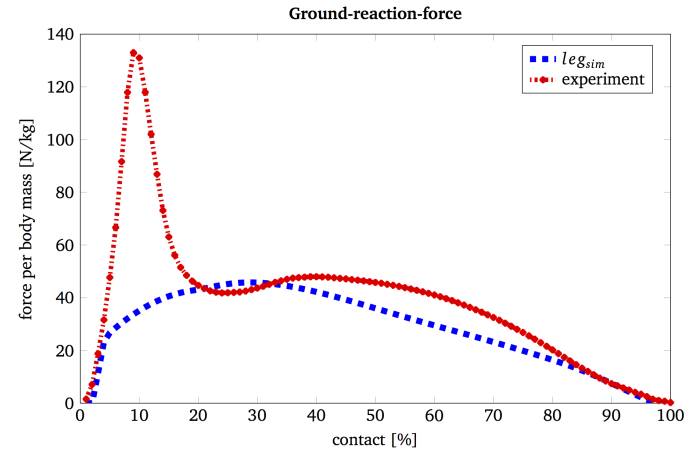
Auf Basis von experimentellen Daten und unter Verwendung eines Genetischer Algorithmus erfolgt die Bestimmung der für die Simulation notwendigen Modellparameter. Diese werden so gewählt, dass eine bestmögliche Übereinstimmung der Bodenreaktionskräfte (GRF) zwischen der Messung und der Simulation beim Absprung erzeugt wird. Das Ergebnis der besten Simulation ist in Abbildung 5 ersichtlich.
Das verwendete Weitsprungmodell erzeugt einen ähnlichen Verlauf der gemessenen Bodenreaktionskräfte. Allerdings ist die hier verwendete Modellstruktur nicht in der Lage die Landedynamik und damit die erste hohe Kraftspitze abzubilden. Lediglich eine zusätzliche viskos-elastisch gelagerte Masse erzeugt ein solches Kraftmuster (Seyfarth et al., 1999; Seyfarth et al., 2000).
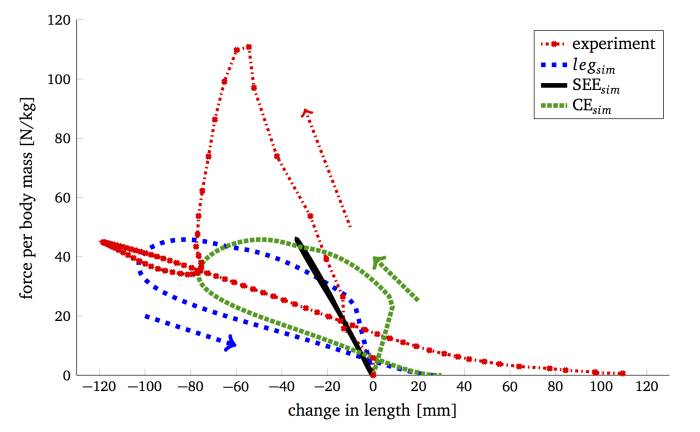
Für die Untersuchung der interagierenden Modellelemente und deren Beitrag an der Sprungleistung wird das Kraft-Längenänderungs-Diagramm herangezogen. In der Abbildung 6 sind die Verläufe der experimentellen Messung sowie die Simulationsergebnisse des Muskelelements (CE) und des seriell elastischen Elements (SEE) während des Absprungs dargestellt.
Dabei stellen die in der Abbildung eingeschlossenen Flächen Energiemenge dar. Ist eine Fläche im Uhrzeigersinn von einem Verlauf eingeschlossen, handelt es sich um eine Energiemenge, die von dem Muskel generiert wird und für die Erzeugung der Bewegung genutzt werden kann. Ist die Fläche durch eine Kurve eingeschlossen, die entgegen dem Uhrzeigersinn verläuft, wird die Energiemenge absorbiert und in eine für die Bewegung nicht mehr nutzbare Form umgewandelt. Hier zeigt sich die energieabsorbierdende Arbeitsweise des Muskels bei einer exzentrischen Beanspruchung.
Aus den experimentellen Daten geht hervor, dass während des Absprungs eine große Energiemenge absorbiert wird. Die Simulation zeigt, dass ein Großteil dieser Energie von dem Muskelelement absorbiert wird. Das Federelement gibt die während des Sprungs aufgenommene Energie wieder ab. Das Muskelelement wird in mehr als 80% der Kontaktzeit verkürzt, sodass eine Dehnung der Muskelfasern vollzogen wird, die in einer exzentrischen Krafterhöhung (siehe MUS3 Kraft-Relationen) resultiert. Dabei wird die Krafterzeugung des Muskelelementes aufgrund der Nachgiebigkeit des elastischen Elements angehoben.
Mit der Verringerung der seriellen Steifigkeit wird der Arbeitspunkt des Muskels verschoben. Aufgrund der dann großen Kompression des Federelements zeigt das Muskelelement eine verminderte Verkürzung, sodass die Muskelfasern nicht so lang gedehnt werden. Dabei werden die Muskelfasern kürzer exzentrisch und länger konzentrisch beansprucht, sodass eine geringere Krafterzeugung des Muskelelements die Folge ist. Zusätzlich erzeugt das Muskelelement eine größere Energiemenge, die zur Unterstützung der Bewegung genutzt wird.
Conclusion
Aus den Simulationsergebnissen können mehrere Schlussfolgerungen gezogen werden. Zunächst ist es möglich mit Hilfe eines vereinfachten Weitsprungmodells die Beinfunktion in axialer Richtung zur Untersuchung der Interaktion von Muskel und Sehne ausreichend zu beschreiben. Durch weitere Anpassungen des Modells ist eine Verbesserung der Modellqualität und damit der Abbildung der Realität möglich. Während des Absprungs hebt das elastische Element die Krafterzeugung des Muskelelements aufgrund der exzentrischen Beanspruchung an. Hierbei wird eine große Energiemenge vom Muskel dissipiert. Wird die Steifigkeit der Elastizität reduziert, ergibt sich eine geringere Krafterzeugung des Muskelelements aufgrund einer Verschiebung des Arbeitspunktes. Jedoch verrichtet das Muskelelement mehr Arbeit, die für die Bewegungserzeugung und damit für die Generation der Absprunggeschwindigkeit genutzt werden kann. Beide Auswirkungen resultieren in einer unterschiedlichen Veränderung der Sprungweite.
Outlook
Weitere Themen für Untersuchungen bzw. offene Fragestellungen sind:
- Erweiterung des Weitsprungmodells um ein Fuss- bzw. Prothesenmodell
- Erweiterung des Weitsprungmodells um ein Dämpfungselement
- Erweiterung des Weitsprungmodells um die Anlaufphase (inkl. Sprungvorbereitung)
- Athletenspezifische Anpassung der Modellparameter und Einsatz des Weitsprungmodells im Rahmen einer Leistungsdiagnostik
- Identifikation des optimalen Arbeitspunktes des Gesamtsystems
- Untersuchung verschiedener Bewegungsaufgaben, wie Hüpfen und Rennen
References
- Bridgett, L. A., & Linthorne, N. P. (2006). Changes in long jump take-off technique with increasingrun-up speed. Journal of sports sciences, 24(8), 889-897.
- Geyer, H., Seyfarth, A., & Blickhan, R. (2003). Positive force feedback in bouncing gaits?. Proceedings of the Royal Society of London. Series B: Biological Sciences, 270(1529), 2173-2183.
- Graham-Smith, P., & Lees, A. (2005). A three-dimensional kinematic analysis of the long jump take-off. Journal of sports sciences, 23(9), 891-903.
- Haeufle, D. F. B., Grimmer, S., & Seyfarth, A. (2010). The role of intrinsic muscle properties for stable hopping—stability is achieved by the force–velocity relation. Bioinspiration & biomimetics, 5(1), 016004.
- Haeufle, D. F. B., Grimmer, S., Kalveram, K. T., & Seyfarth, A. (2012). Integration of intrinsic muscle properties, feed-forward and feedback signals for generating and stabilizing hopping. Journal of The Royal Society Interface, 9(72), 1458-1469.
- Hay, J. G., Miller, J. A., & Canterna, R. W. (1986). The techniques of elite male long jumpers. Journal of biomechanics, 19(10), 855-866.
- Linthorne, N. P. (2010). Biomechanics of the long jump. Routledge Handbook of Biomechanics and Human Movement Science, 340.
- Nagano, A., Komura, T., & Fukashiro, S. (2004). Effects of series elasticity of the muscle tendon complex on an explosive activity performance with a counter movement. Journal of Applied Biomechanics, 20(1), 85-94.
- Nolan, L., & Lees, A. (2000). Touch-down and take-off characteristics of the long jump performance of world level above-and below-knee amputee athletes. Ergonomics, 43(10), 1637-1650.
- Rabita, G., Couturier, A., & Lambertz, D. (2008). Influence of training background on the relationships between plantarflexor intrinsic stiffness and overall musculoskeletal stiffness during hopping. European journal of applied physiology, 103(2), 163-171.
- Rode, C., Siebert, T., & Blickhan, R. (2009). Titin-induced force enhancement and force depression: A ‘sticky-spring’mechanism in muscle contractions?. Journal of theoretical biology, 259(2), 350-360.
- Seyfarth, A., Friedrichs, A., Wank, V., & Blickhan, R. (1999). Dynamics of the long jump. Journal of biomechanics, 32(12), 1259-1267.
- Seyfarth, A., Blickhan, R., & Van Leeuwen, J. L. (2000). Optimum take-off techniques and muscle design for long jump. Journal of Experimental Biology, 203(4), 741-750.
- Van Leeuwen, J. L. (1992). Muscle function in locomotion. Mechanics of animal locomotion, 11, 191-249.