Inhaltsverzeichnis
2018 Sarah Dorsch
Sensorimotor processing of a neuromechanical hopping model
| Title | Sensorimotor processing of a neuromechanical hopping model |
|---|---|
| Titel | Sensomotorische Verarbeitung in einem Neuromechanischen Hüpfmodell |
| Supervisor | M.Sc. Christian Schumacher, Dr.-Ing. Philipp Beckerle, Prof. Dr. phil. André Seyfarth |
| Autor | Sarah Dorsch |
| Department | FB 16 Mechanical Engineering |
| Last revision | 30.06.2019 |
| Status | finished |
Einleitung
Viele Bewegungen im täglichen Umfeld sind für den Menschen selbstverständlich und geschehen häufig automatisiert. Gehen wir auf unebenem Gelände oder über Kopfsteinpflaster, ist es trotz der sich ändernden Umgebung nicht notwendig, dass wir uns gedanklich auf die Ausführung konzentrieren. Ebenso unter anderen Bedingungen, wie beim Tragen eines Korbes, was eine einseitige zusätzliche Masse bedeutet, können wir uns häufig ohne Schwierigkeiten fortbewegen. Intuitiv scheinen wir unter den veränderten Bedingung unseren Gang zu stabilisieren und anzupassen. Dies kann bewältigt werden, obwohl die Beine eines Menschen nicht exakt gleich sind. Beispielsweise haben viele Menschen unterschiedlich lange Beine (Gurney, 2002).
Zur Entwicklung von Prothesen, Orthesen, Exoskeletten und Robotern stellt sich die Frage, wie der Mensch sich an seine Umgebung anpasst, um diese Regelstrategien nachbilden und auf ein technisches System übertragen zu können. Um sich diesem Thema anzunähern, wird hier das Hüpfen auf der Stelle untersucht, welches der vertikalen Schwingung der Lokomotion entspricht (Häufle et al., 2010).
Es fragt sich, welchen Einfluss beispielsweise die im Alter verringerte Muskelkraft auf unsere Bewegung hat (Hortobágyi und Devita, 2000). Oder wie wir unsere Bewegung auf unebenen Untergründen anpassen, z. B. auf Kopfsteinpflaster. Auch das Laufen auf weichem Untergrund wie Gras, also ein nachgiebiger Boden, stellt eine alltägliche Bewegung unter Störung dar.
Ziel ist es, die Robustheit eines reflex-nutzenden neuromechanischen Hüpfmodells nach Geyer (Geyer et al., 2003) mittels simulativ aufgeprägter Störungen zu analysieren. Dabei werden sowohl sensorische als auch mechanische Störungen betrachtet. Das Störverhalten wird anschließend anhand von Kriterien quantifiziert, die die Stabilität, die Performance und die Effizienz des Hüpfmusters beschreiben. In der Literatur wird angedeutet, dass der Bereich des stabilen Gehens und Rennens durch simulierte Asymmetrien zwischen den Beinen nicht zwangsläufig verringert wird und sogar für spezielle Asymmetrien des Beinwinkels beim Auftreten erweitert werden kann (Merker et al., 2015; Merker et al., 2011). Hierdurch und durch die Gegebenheiten in der Realität motiviert, wird das Hüpfverhalten unter asymmetrischen Bedingungen betrachtet. Dazu wird das gegebene Hüpfmodell um ein zweites Bein erweitert. Anschließend wird anhand von Bodenhöhenvariationen untersucht, in welchem Maße Störungen ausgeglichen werden können und ob sich dies in Abhängigkeit der Feedbackkonfiguration verändert. Des Weiteren wird an diesem Beispiel das Modell validiert, indem ein Vergleich der vorausgesagten Beinsteifigkeit mit experimentellen Ergebnissen angestellt wird. Zuletzt wird geprüft, ob eine adaptive Einstellung der Reflexparameter das Störverhalten verbessern kann. Diese Erkenntnisse können genutzt werden, um die Qualität von Assistenzsystemen, wie Prothesen und Orthesen, zu steigern, indem z. B. an den Menschen angepasste Regelungen verwendet werden.
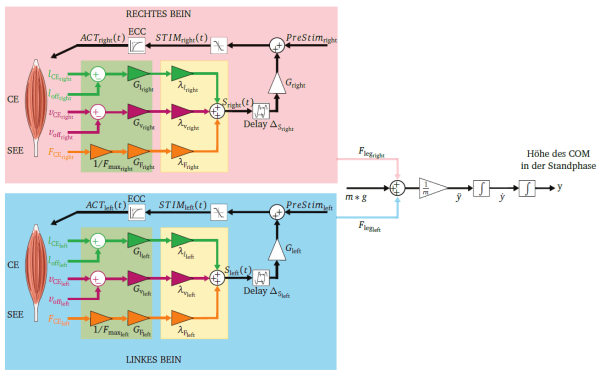
Reflektorisches Hüpfmodell
Für die Simulationen in dieser Arbeit wird das reflektorische Hüpfmodell nach Geyer (2003) verwendet. Es besteht aus einem masselosen, zweisegmentigen Bein (jeweils der Länge $l_{\text{s}}$) mit einem masselosen Knieextensormuskel mit Sehne sowie einem Körper, der auf einen Massenpunkt der Masse $m$ vereinfacht ist. Der Muskelsehnenkomplex MTC besteht aus einem kontraktilen CE und einem seriell elastischen Element SEE. Die Kraft-Längen-Funktion $f_{\text{l}}( l_{\text{CE}})$ und die Kraft-Geschwindigkeits-Funktion $f_{\text{v}}( v_{\text{CE}})$ werden hillförmig angenommen. Nach dem Produktansatz ergibt sich die erzeugte Kraft $F_{\text{CE}}$ aus:
\begin{equation}
F_{\text{CE}}=ACT \cdot f_{\text{l}}( l_{\text{CE}})\cdot f_{\text{v}}( v_{\text{CE}})\cdot F_{\text{max}}
\end{equation}
Die Aktivierung des Muskels $ACT$ kann durch Feedforward und/oder Feedback (Kraft- (FFB), Längen- (LFB) oder Geschwindigkeitsfeedback (VFB)) erzeugt werden.
Zusätzlich wird eine Erweiterung dieses Modells nach Schumacher (2017) genutzt, die eine Vermischung der Feedbacks (Blending) zur Bildung der Aktivierung ermöglicht. Der Anteil der einzelnen Feedbacks wird über sogenannte Blendingfaktoren $\lambda_{\text{F}} \text{, } \lambda_{\text{L}} \text{, } \lambda_{\text{V}} $ bestimmt, deren Summe eins ergibt.
Hierdurch ergibt sich das Signal $S(t)$, welches nach Verzögerung $\Delta_{\text{S}}$ und Verstärkung $G$ über eine Differentialgleichung erster Ordnung (ECC) zur Aktivierung $ACT$ führt (siehe Abbildung 1):
\begin{equation}
S(t)=\lambda_{\rm{F}} \cdot G_{\rm{F}} \cdot \frac{F_{\rm{CE}}}{F_{\rm{max}}}+\lambda_{\rm{L}} \cdot G_{\rm{L}} \cdot (l_{\rm{CE}}-l_{\rm{off}})+\lambda_{\rm{V}} \cdot G_{\rm{V}} \cdot (v_{\rm{CE}}-v_{\rm{off}})
\end{equation}
Um auch Asymmetrien zwischen den Beinen untersuchen zu können, wird dieses Modell hier um ein zweites Bein erweitert. Die Bewegungsgleichung unterteilt nach Stand- und Flugphase ergibt sich damit wie folgt:
\begin{equation}
\begin{split}
& m \ddot{y}=-m g+F_{\rm{leg}_{right}}+F_{\rm{leg}_{left}} \hspace{0.98cm} \text{für Standphase}\\
& m \ddot{y}=-m g \hspace{4.1cm} \text{für Flugphase}
\end{split}
\end{equation}
Robustheit des Hüpfmodells gegen dauerhafte Störungen
Um das Störverhalten des Hüpfmodells zu untersuchen, werden verschiedene mechanische und sensorische Störungen aufgeprägt und die Auswirkung auf verschiedene Größen (Untersuchungskriterien) analysiert. Dabei werden sowohl Störungen beider Beine (symmetrisch) als auch Variationen von nur einem Bein (asymmetrisch) getestet.
Untersuchungskriterien
Zur Analyse der Stabilität wird die Anzahl der Sprünge ausgewertet. Es wird definiert, dass stabiles periodisches Hüpfen
durch das Modell vorhergesagt wird, wenn mindestens 50 Absprünge vorhergesagt werden (Schumacher, 2017).
Der Status wird genutzt, um das jeweilige Modellverhalten zu beschreiben. Werden 50 Absprünge nicht erreicht, wird unterschieden zwischen: Hinfallen, Stehenbleiben und Schwingen. Letzteres ist definiert als ein Schwingen des Massenschwerpunkts, ohne dass ein gleichzeitiges Abheben beider Beine beobachtet werden kann. Bei Erreichen der 50 Absprünge werden zwei Fälle unterschieden. Zum einen das quasi-stabile Hüpfen, wenn sich die letzten fünf Maxima der Schwerpunktbewegung unterscheiden und zum anderen stabiles Hüpfen, bei dem 50 Hüpfer durchgeführt werden und die letzten fünf Maxima den gleichen Wert haben.
Um die Performance zu quantifizieren wird die Hüpfhöhe $\boldsymbol{\Delta h_{\rm{max}}}$ bestimmt. Hierzu werden, falls 50 Absprünge erreicht wurden, die Maxima der Schwerpunktbewegung bestimmt. Die Hüpfhöhe ergibt sich dann aus der Höhe des Massenschwerpunkts im Maximum abzüglich der Beinlänge.
Als weiteres Kriterium zur Charakterisierung der Performance wird die Hüpffrequenz $\boldsymbol{f_{\rm{hop}}}$ herangezogen. Sie
berechnet sich aus dem Verhältnis der Simulationszeit und der Anzahl an Sprüngen.
Das Beinverhalten kann durch eine lineare Feder abgebildet werden, wobei die Beinsteifigkeit $\boldsymbol{k_{\rm{leg}}}$ aus dem Verhältnis von maximaler Beinkraft und maximaler Kompression des Beins berechnet wird: $k_{\rm{leg}}=F_{\rm{leg_{max}}}/\Delta l_{\rm{leg}}$ (Farley und Morgenroth, 1999). Die Gesamtsteifigkeit beider Beine ergibt sich aufgrund der parallelen Anordnung aus der Summe beider Beinsteifigkeiten.
Zur Quantifizierung der Effizienz des Hüpfens wird die metabolische Effizienz $\boldsymbol{\eta}$ bestimmt, die sich aus dem Verhältnis von mechanischer Energie und metabolischem Aufwand des CE berechnet. (Schumacher, 2017; Krishnaswamy, 2011)
Zuletzt wird das Verhältnis der maximalen Arbeit des kontraktilen Elements zur maximalen Arbeit des gesamten Muskelsehnenkomplexes $\boldsymbol{\alpha_{\rm{k}}}$ betrachtet.
Störungen
Diese Untersuchungskriterien werden unter dem Einfluss von ausgewählten Störungen betrachtet. Tabelle 1 zeigt die untersuchten Störungen und die dazugehörigen Störstufen. Diese werden, abgesehen von der Bodensteifigkeit, jeweils für das linke Bein (asymmetrisch) und
für beide Beine (symmetrisch) eingestellt. Durch den Vergleich von asymmetrischer und symmetrischer
Störung lässt sich der Einfluss der Asymmetrie auf das Störverhalten erkennen.
| Tabelle 1: Untersuchte Störungen mit gewählter Höhe der Störung | ||||
| Klassifizierung | Störung | Initialwert | Störstufe 1 | Störstufe 2 |
|---|---|---|---|---|
| sensorische Störung | Reflexparameter ($G_{\rm{F}},\text{ } G_{\rm{L}},\text{ } l_{\rm{off}},\text{ } G_{\rm{V}},\text{ } v_{\rm{off}}$) | optimal | $-20\,\%$ | $+20\,\%$ |
| sensorische Störung | Delay ($\Delta_{\rm{p}},\Delta_{\rm{F}},\Delta_{\rm{L}},\Delta_{\rm{V}}$) | $15\,\text{ms}$ | $50\,\text{ms}$ | $70\,\text{ms}$ |
| sensorische Störung | Rauschen ($N_{\rm{all}},N_{\rm{F}},N_{\rm{L}},N_{\rm{V}}$) | kein Rauschen | $\text{SNR}=10\,\text{dB}$ | $\text{SNR}=20\,\text{dB}$ |
| mechanische Störung | Segmentlänge ($l_{\rm{seg}}$) | $0,5\,\text{m}$ | $0,48\,\text{m}$ | $0,52\,\text{m}$ |
| mechanische Störung | Bodensteifigkeit ($k_{\rm{ground}}$) | $9999\,\frac{\text{kN}}{\text{m}}$ | $500\,\frac{\text{kN}}{\text{m}}$ | $100\,\frac{\text{kN}}{\text{m}}$ |
Sensor-Motor-Maps
Zur Untersuchung des Einflusses der Störungen auf die Untersuchungskriterien werden sogenannte Sensor-Motor-Maps (SMM) verwendet (Schumacher, 2017). Durch sie ist eine Visualisierung des dreidimensionalen Raums der Blendingfaktoren in einem zweidimensionalen Koordinatensystem möglich.
Es handelt sich dabei um Dreiecke, wobei verschiedenen Positionen im Dreieck unterschiedliche Reflexkombinationen (Blendings) zugeordnet werden. Die Ecken der Karte entsprechen den isolierten Reflexen, d. h. oben wird reines FFB, links isoliertes VFB und rechts alleiniges LFB verwendet. Umso größer die Entfernung zum jeweiligen Eckpunkt ist, desto kleiner der Anteil des Feedbacks. Im Mittelpunkt haben damit alle Feedbacks den gleichen Anteil.
Um den Einfluss von Störungen zu untersuchen, können die Topologien der erstellten Sensor-Motor-Maps ohne und mit der Störung verglichen werden.
Die für die Kartierung verwendeten initialen Reflexparameter, also die Gains der Feedbacks $G_{\text{F}}$, $G_{\text{L}}$ und $G_{\text{V}}$ sowie die Offsets $l_{\text{off}}$ und $v_{\text{off}}$, werden mit Hilfe von Optimierung (Pattern-Search) bestimmt. Als Optimierungskriterien werden die Stabilität (Erreichen von 50 Sprüngen) und die Performance (Hüpfhöhe) gewählt. Es liegt nahe, dass Menschen beim Erlernen von Bewegungen nicht nur einzelne Parameter in Isolation beachten, sondern vielfältige sensorische Signale verarbeiten, um die gewünschte Aufgabe möglichst gut zu erfüllen. Daher findet die Optimierung bei gleichen Anteilen aller Feedbacks ($\lambda_{\rm{F}}=\lambda_{\rm{L}}=\lambda_{\rm{V}}=1/3$) statt. Im Optimum sind LFB und FFB positiv, VFB negativ.
Ergebnisse der Störuntersuchungen
Für die Variationen der Feedbackgains, des VFB-Offsets, bei Verrauschen des FFB und des VFB sowie
bei Beinlängen- und Bodensteifigkeitsveränderungen bleiben die Kartierungen sowohl für die Stabilität
als auch für die anderen Hüpfcharakteristiken nahezu erhalten. Die Störung des LFB-Offsets, das
Hinzufügen von Delays in allen getesteten Kombinationen sowie Rauschen des LFB oder aller Feedbacks
verändert sowohl das Stabilitätsgebiet als auch die betrachteten Hüpfcharakteristiken. Abgesehen vom
Delay entstehen die Änderungen des Stabilitätsgebiets durch einen weiteren Instabilitätsbereich, für
den Stehenbleiben vorhergesagt wird, wie in Abbildung 2 am Beispiel des LFB-Offsets gezeigt. Nahe diesem Bereich ist hierdurch auch die Performance und
damit auch die anderen Hüpfcharakteristiken stark beeinflusst.
Für die Verzögerung des FFB und des LFB wird zudem eine stark erhöhte Performance
vorhergesagt, während die Performance bei Verzögerung des VFB deutlich abnimmt.
Das Stabilitätsverhalten der meisten
symmetrischen Störungen ergibt sich aus der Superpositionierung zweier asymmetrisch variierter
Beine, sodass die Veränderung des Verhaltens durch die symmetrische Störung lediglich gegenüber der
asymmetrischen Störung verstärkt wird. Für die Asymmetrie des Delays des VFB oder aller Feedbacks gilt dies nicht. Hier wird der
Effekt der einbeinigen Störung nicht durch zusätzliche Störung des zweiten Beins verstärkt, sondern
die Verbesserung wieder abgeschwächt (vergleiche Abbildung 3).

Diskussion der Störuntersuchungen
Hüpfverhalten des zweibeinigen Modells im ungestörten Fall
Auch in Schumacher (2017) wurden Sensor-Motor-Maps zur Untersuchung des Störverhaltens erstellt. Im Gegensatz
zu dieser Arbeit wurden die Feedbackparameter dort aber mittels einer Optimierung der Performance
der isolierten Feedbacks eingestellt, was zu positiven Feedbacks führt. Daher unterscheiden sich die Topologien der Karten von den hier
vorgestellten. Dennoch ist das Stabilitätsgebiet auch hier zusammenhängend. Auffällig ist allerdings,
dass in Schumacher (2017) die Stabilitätsgrenze bei wenig performanten Blendings liegt, während in dieser Arbeit eine
Steigerung der Performance bis zur Stabilitätsgrenze festgestellt werden kann.
In Geyer (2005) wird ebenso beobachtet, dass das negative VFB zum einen die Performance verstärkt, zum
anderen aber eine destabilisierende Wirkung hat. Eine ansteigende Hüpfhöhe resultiert in einer höheren
Dehnungsgeschwindigkeit des Muskels kurz nach dem TD. Durch das negativ verstärkte Feedback wird
das Ansteigen der Muskelaktivierung verzögert. Dies erzeugt eine noch höhere Hüpfhöhe, da das Modell
weiter einsinken kann. Dementsprechend wird die Hüpfhöhe und damit die TD-Geschwindigkeit immer
höher. Es existiert dann ein kritischer Punkt der TD-Geschwindigkeit, der das Bein zusammenbrechen
lässt, da die Verzögerung der Aktivierung schließlich zu groß wird und das schnelle Absinken des
Massenschwerpunkts nicht mehr durch die Aktivierung unterbunden wird. Dies könnte der Grund
dafür sein, dass in den Sensor-Motor-Maps dieser Arbeit eine harte Grenze entsteht.
Robustheit des zweibeinigen Modells gegenüber sensorischen und mechanischen Störungen
Für die untersuchten Störungen kann insgesamt festgehalten werden, dass robuste Sensor-Motor-Maps
gefunden wurden. Der Stabilitätsbereich wurde nicht zerklüftet und es existiert ein großer, zusammenhängender
Bereich für stabiles Hüpfen.
Größere Veränderungen des Hüpfverhaltens können bei Variation des Offsets des Längenfeedbacks
beobachtet werden.
Die Offsets spiegeln die Sensitivität der Sensoren wider (Prochazka und Ellaway, 2012).
Durch $l_{\text{off}}$ wird daher eine frühzeitige Aktivierung des Muskels unterdrückt (Geyer et al., 2003; Schumacher, 2017). Bei
einem verringertem $l_{\text{off}}$ wird somit die Absenkung des Massenschwerpunkts frühzeitig gestoppt, da der Muskel bereits aktiviert ist und zu kontrahieren beginnt. Hierdurch ist auch die Zeit zur Beschleunigung bis zum TO verkürzt, wodurch eine geringere Geschwindigkeit im TO erreicht wird
und damit ein deutlicher Einfluss auf die Performance entsteht.
Die Variation von $v_{\text{off}}$ hat hingegen nur sehr wenig Einfluss auf die Sensor-Motor-Maps, was daran liegen könnte, dass der Offset besonders zu Beginn starken Einfluss auf die Aktivierung hat, wenn die Kraft-Geschwindigkeits- und die Kraft-Längen-Funktion noch in Bereichen geringer Kraft sind.
Wie auch in Geyer (2005) gefunden, können die Verzögerung von positivem FFB und positivem LFB die Performance verbessern. Die Verzögern des negativen VFB hingegen führt zu einer verschlechterten Performance.
Außerdem werden die Stabilitätsbereiche durch Verzögern von FFB und LFB verkleinert, was darauf hindeutet, dass das Hüpfverhalten bei äußeren Störungen leichter destabilisiert wird.
Die SMM bei Rauschen aller Feedbacks wird hauptsächlich durch das Rauschen des LFB beeinflusst werden. Beim Verrauschen des FFB und des VFB veränderte sich das Hüpfverhalten kaum. Durch das Rauschen wird $l_{\text{off}}$
immer wieder überschritten, was eine frühzeitigen Aktivierung des Muskels auslöst, wodurch die Performance abnimmt. Aufgrund der frühere Aktivierung durch das LFB wird der verzögerten Aktivierung durch das VFB entgegengewirkt und damit die kritische Grenze des VFB verschoben.
Bei verringerter Bodensteifigkeit konnte eine Erhöhung der Performance und eine verringerte Beinsteifigkeit festgestellt werden. Diese Ergebnisse entsprechen dem Störverhalten des einbeinigen Modells in Schumacher (2017). Allerdings widersprechen sie experimentellen Ergebnissen. In Ferris und Farley (1997) konnte gezeigt werden, dass der Mensch bei unterschiedlichen Bodensteifigkeiten die Beinsteifigkeit anpasst, sodass die Gesamtsteifigkeit aus Bein und Boden konstant bleibt, also bei einer Verringerung der Bodensteifigkeit eine höhere Beinsteifigkeit hat.
Dies deutet darauf hin, dass der Mensch Anpassungsmechanismen hat, die durch das Modell nicht abgebildet wurden.
Störverhalten bei asymmetrisch aufgeprägten Störungen
Für die meisten getesteten Asymmetrien kann festgestellt werden, dass das Hüpfverhalten nicht durch
die Asymmetrie selbst beeinflusst wird, sondern die Störung das veränderte Hüpfverhalten verursacht,
sodass sich bei symmetrischer Störung lediglich die Änderung verstärkt.
Besonders auffällig ist, dass eine asymmetrische Aufschaltung eines Delays zu einem vergrößerten Stabilitätsgebiet führt. Die Kombination aus „schnellem“ und „langsamem Bein“ scheint eine stabilisierende Wirkung für Blendings mit ähnlichen Anteilen aller Feedbacks zu haben. Die kurz nacheinander aktivierierenden Muskeln der zwei Beine führen wie die in anderen Winkeln aufkommenden Beine bei der Untersuchung von Merker (2011) zu einer Stabilisierung von im Referenzfall instabilen Feedback
zusammensetzungen. Die Stabilität wird somit durch die Asymmetrie verbessert, jedoch wird dadurch das Systemverhalten schwieriger voraussagbar, da häufig quasi-stabiles Hüpfen auftritt und es kommt zu Einbußen der Performance.
Für die asymmetrische Erhöhung von $l_{\text{off}}$ wird bei Blendings nahe des isolierten LFB Stehenbleiben vorausgesagt. Dies kann bei symmetrischer Erhöhung nicht gefunden werden. Durch die Erhöhung des Offsets wird der Muskel des linken Beins erst später aktiviert als der des rechten Beins. Entgegen der sonst auf die Performance positiv wirkenden Verzögerung der Aktivierung, führt dies hier vermutlich
dazu, dass das Hüpfen hauptsächlich aus dem rechten Bein entsteht und das linke Bein schon kurz nach Anstieg der Aktivierung wieder abhebt. Es kommt dann zum Stehenbleiben, wenn die Aktivierung des linken Beins so gering zum Hüpfen beiträgt, dass das Modell den TO nicht mehr erreicht und daraufhin
stehenbleibt. Das Stehenbleiben bei der asymmetrischen Beinlängenveränderung ergibt sich vermutlich aus ähnlichen Prozessen.
Zweibeiniges Hüpfen mit Bodenhöhenstörungen
Im letzten Abschnitt wurden Tendenzen festgestellt, wie sich das Hüpfverhalten durch Einprägen von Störungen verändert. Dies wird in diesem Abschnitt erweitert. Dazu wird die Kapazität des Modells, Störungen auszugleichen, anhand von Bodenhöhenvariationen bei verschiedenen Feedbackzusammensetzungen untersucht. Außerdem wird anhand der Beinsteifigkeit bei dieser Störung das Modellverhalten mit experimentellen Ergebnissen verglichen.
Bei der Untersuchung von Bodenhöhenveränderungen ist von besonderem Interesse, wie sich unterschiedliche Beiträge und Signalpfade der Feedbacks sowie unterschiedliche Optimierungsziele auf das Störverhalten auswirken. Dazu wird die Robustheit des Hüpfverhaltens mit performance-optimierten isolierten Reflexen und mit performance-optimiertem geblendeten Feedback gegenübergestellt. Des Weiteren wird für den geblendeten Fall untersucht, wie sich ein geändertes Optimierungsziel (optimale Effizienz) auf das Störverhalten auswirkt.
Die Bodenhöhenveränderung wird jeweils im Apex eingestellt. Es werden Änderungen im Bereich $[-0,8 \,\text{m};+0,8\,\text{m}]$ in $0,005 \,\text{m}$ Schritten untersucht.
Für den Vergleich von Simulation und Experiment werden unveröffentlichte Daten von Dario Tokur
(Institut für Sportwissenschaften, TU Darmstadt) verwendet. In den Experimenten wurden unerwartete Bodenabsenkungen durchgeführt. Die Probanden hüpfen dazu auf einer Kraftmessplatte. Des Weiteren werden Marker an verschiedenen Stellen des Körpers positioniert, deren Lage während dem Hüpfen durch ein Motion Capture System erfasst wird.
Der Mensch bevorzugt meist Bewegungen mit geringen metabolischen Kosten (McNeill, 2002). Daher werden für den Vergleich zwischen Experiment und Modell effizienz-optimierten Feedbackparameter herangezogen. Als Vergleichsgröße wird die Beinsteifigkeit gewählt, da sie zum einen ein entscheidender Parameter der Dynamik des Rennens ist (Ferris, Louie und Farley, 1998) und zum anderen leicht berechnet werden kann.
Simulative Ergebnisse der Störversuche bei Bodenhöhenvariationen
Für alle simulierten Bodenhöhenänderungen wurde nach der Störung entweder stabiles Hüpfen oder
Hinfallen detektiert. Zudem erreicht das Modell nach der Störung wieder die gleiche Hüpfhöhe.
Die größten Bodenanhebungen können durch das performance-optimierte geblendete Feedback
stabilisiert werden, während isoliertes performance-optimiertes FFB die geringsten
Erhöhungen ausgleicht (Abbildung 4).
Das performance-optimierte geblendete Feedback führt zur höchsten Sensibilität des Modells auf
Bodenabsenkungen. Das performance-optimierte LFB stabilisiert Bodenabsenkungen am besten.
Werden die Feedbackparameter im geblendeten Fall effizienz-optimiert eingestellt, führt dies zu einer größeren Robustheit gegenüber Bodenabsenkungen.
Vergleich des Störverhaltens von Modell und Mensch
Wie durch die Simulation vorhergesagt, können die Probanden die Bodenhöhenveränderung ausgleichen. Sie hüpfen nach der Bodenabsenkung mit annähernd gleicher Hüpfhöhe.
Auch die Beinsteifigkeit wird nach der Störung wieder wie vor der Störung eingestellt.
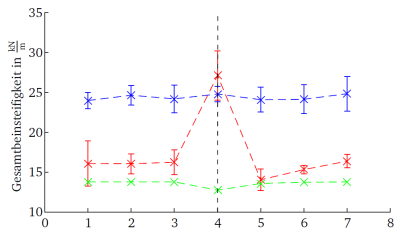
Im gestörten Sprung selbst, weichen die Steifigkeiten sowohl für das Modell als auch für Proband 2 von der ungestörten Steifigkeit ab. Das Modell hat in diesem Sprung eine verringerte Steifigkeit, hingegen ist die des Probanden erhöht (Abbildung 5). Dabei ist die Verringerung beim Modell wie auch die Erhöhung beim Probanden umso stärker, je größer die Bodenabsenkung ist. Proband 1 zeigt keine generelle Anpassung der Steifigkeit.
Diskussion
Fallrisiko durch Bodenhöhenänderung bei verschiedenen Reflexparametern
Allgemein kann festgehalten werden, dass weniger performante Feedbacks eine größere Robustheit gegenüber Bodenabsenkungen aufweisen. Ist die Performance des Systems hoch, ist auch die potentielle Energie im Apex hoch und damit die TD-Geschwindigkeit höher als bei weniger performanten Einstellungen. Wird nun zusätzlich noch weitere Energie durch eine Bodenabsenkung hinzugefügt, wird das Bein noch weiter gebeugt und damit der Muskeln überdehnt. Vermutlich befindet sich der Muskel dann in Bereichen, in denen aufgrund der Kraft-Längen-Funktion nur noch geringe Kräfte erzeugt werden können. Daher kollabiert das Modell in der Standphase. Dies zeigt, dass unterschiedliche Feedbackblendings und Parametereinstellungen für verschiedene Aufgaben besser geeignet sind.
Diskussion des Vergleichs von Simulation und Experiment
Die Anpassungsstrategien des Menschen bei unterschiedlich nachgiebigem Boden sind häufig diskutiert. Für weicher werdenden Boden nimmt die Beinsteifigkeit zu. (Moritz und Farley, 2004),(Ferris und Farley, 1999)
Wird die Bodenhöhenabsenkung als unendlich nachgiebiger Boden betrachtet, so sollte die Beinsteifigkeit bei Aufkommen auf dem unerwarteten Boden stark erhöht sein. Dies kann im Experiment für Proband 2 festgestellt werden (Abbildung 5).
In Müller und Blickhan (2010) werden weitere Experimente durchgeführt, bei denen Probanden Stufen von 10 cm sowohl
auf- als auch abwärts rennen. Bei der Erhöhung des Bodens ist die Beinsteifigkeit umso geringer, je größer der Bodenanstieg eingestellt wird. Dies entspricht der in der Literatur bekannten Anpassung der Beinsteifigkeit auf steifer werdendem Boden. Für das Abwärtslaufen wird allerdings eine annähern konstante Beinsteifigkeit gefunden. Dieses Ergebnis ist in Übereinstimmung mit der Reaktion von Proband 1 auf die Bodenhöhenstörung.
Dennoch springt Proband 1 auch in den ungestörten Sprüngen mit ungewöhnlich hohen Beinsteifigkeiten für bevorzugtes Hüpfen. Sie beträgt etwa 24 kN/m , während in Farley und Morgenroth (1999) von einer Beinsteifigkeit von etwa 14,5 kN/m bei präferierter Hüpfhöhe berichtet wird. Es ist möglich, dass der Proband seine Beine dauerhaft versteift hat, da er dem Fallrisiko entgegenwirken wollte.
Außerdem sind die oben angeführten Experimente beim Rennen durchgeführt worden. Nicht alle Ergebnisse und Regelstrategien des Menschen beim Gehen oder Rennen sind auf das Hüpfen übertragbar (Darley und Biewener, 2006). Da die Ergebnisse der Probanden so stark voneinander abweichen, sollten zur Untersuchung der Anpassungsstrategie des Menschen bei Bodenhöhenvariationen weitere Probandenversuche durchgeführt werden.
Unabhängig davon, ob die Ergebnisse von Proband 1 oder 2 betrachtet werden, verändert sich die
Beinsteifigkeit des Modells in anderer Weise. In der Standphase nach der Störung ist für beide Probanden die GRF erhöht. Dies deutet daher auf eine höhere Hierarchiebene der motorischen Kontrolle, z. B. durch höhere Gehirnareale, zur Einstellung der Beinsteifigkeit hin. Das Reafferenzprinzip (Wolpert und Flanagan, 2001) stellt ein Regelkonzept dar, welches hilft, erwartete Reize zu unterdrücken, sodass höher relevante Reize, z. B. unerwartete, verstärkt werden. Dazu werden eigene Bewegungen aus der sensorischen Information herausgerechnet. Dies würde für das Hüpfen bedeuten, solange die Bewegung wie erwartet ausgeführt wird, stabilisiert die unterste Ebene die Bewegung und die Reize, die hierbei auf den Menschen einwirken, werden unterdrückt. Kommt es zu einer von der Erwartung abweichenden Bewegung, wie frühzeitiges oder verspätetes Aufkommen, wird dies von übergeordneten Zentren ausgeglichen. Dies könnte eine Erklärung für die veränderte Steifigkeit gegenüber dem Modell sein.
Adaptive Reflexparameter
In den letzten Abschnitten konnte festgestellt werden, dass das Störverhalten von der Einstellung der Feedbackparameter
sowie von der Feedbackzusammensetzung zur Aktivierung des Muskels abhängt. Des Weiteren hat der Vergleich zwischen Simulation und Experiment ergeben, dass die Regulation der Beinsteifigkeit des Menschen durch Feedbacks mit konstanten Parametern nicht abgebildet werden kann. Daher wird für das reflexbasierte Modell eine übergeordnete Regelung benötigt, die eine Anpassung der Beinsteifigkeit nachempfindet. Hierzu wird zunächst eine lineare
Anpassung der Feedbackverstärkung an die Fallhöhe getestet (in Anlehnung an Blum, Rummel und Seyfarth (2007)).
Die in der Simulation beobachtete verringerte Gesamtbeinsteifigkeit ist eine Folge einer stärkeren Beinverkürzung. Dies führt letztendlich dazu, dass das Modell bei einer zu hohen Bodenabsenkung hinfällt, da das Bein zu stark verkürzt wird. Aufgrund dieser Verkürzung wird der Muskel überdehnt, wodurch die Kraft-Längen-Funktion sich in einem Bereich befindet, in dem nur geringe Kräfte erreicht werden können. Auch eine große Aktivierung führt dann aufgrund des multiplikativen Zusammenhangs nur zu geringen Muskelkräften. Um bei verringerter Bodenhöhe und damit höherer TD-Geschwindigkeit das zu starke Einsinken zu verhindern, muss die Aktivierung früher ansteigen, was mit einer höheren Beinsteifigkeit einhergeht.
Die Erhöhung der Muskelaktivität bei unerwartet tiefem Fallen konnte auch in experimentellen
Versuchen gezeigt werden (Donelan und Kram, 2001). Des Weiteren wird in der Literatur angedeutet, dass der Mensch
die Feedbackparameter aufgabenabhängig anpasst (Prochazka, Gillard und Bennett,1997). Daher ist zu vermuten, dass dies auch bei
verschiedenen Störungen, wie einer tieferen Fallhöhe, passiert. Ziel ist daher, die Erhöhung der
Beinsteifigkeit durch einen früheren Anstieg der Muskelaktivität, um höhere TD-Geschwindigkeiten
abbremsen zu können und damit größere Bodenabsenkungen auszugleichen. Dies soll durch Anpassung
der Feedbackparameter erreicht werden.
Eine höhere Beinsteifigkeit kann beispielsweise durch Erhöhung von $G_{\text{F}}$ erreicht werden. Da das Modell sich in der
Flugphase im freien Fall befindet, sind Falldauer und Falltiefe proportional. Je höher die Falltiefe, desto
früher muss der Muskel nach dem TD aktivieren, um das Fallen abbremsen zu können. Daher soll $G_{\text{F}}$
mit der Falldauer zunehmen, sodass nach dem TD die Aktivierung früher ansteigt.
Zunächst werden zwei lineare Zusammenhänge zwischen Gain und Fallzeit getestet. Erster Zusammenhang weist eine geringe Steigung auf, der zweite eine deutlich höhere, wodurch höhere Bodenabsenkungen ausgeglichen werden können. Allerdings können nur noch kleine Bodenanhebungen
stabilisiert werden. Sogar für die ursprüngliche Loslasshöhe von 1,05 m, was im Apex einer Bodenanhebung von 0,11 m entspricht, ist diese Interpolation nicht stabil. Daher wird zusätzlich eine Anpassung des Gains
gesucht, die im Bereich kleiner Bodenhöhenvariationen kleine Steigungen aufweist, im Bereich großer
Variationen aber zu großen Änderungen von $G_{\text{F}}$ führt. Dies kann durch einen exponentiellen Zusammenhang erfüllt werden.
Ergebnisse der adaptiven Einstellung
Während die zweite lineare Interpolation sehr hohe Bodenabsenkungen toleriert, ändert die erste lineare
Anpassung des Gains den Stabilitätsbereich kaum (Abbildung 6). Beide Anpassungsstrategien führen
zu einer verringerten Robustheit gegenüber Bodenanhebungen, wobei dieser Effekt für die zweite Interpolation
stärker ist. Die exponentielle Anpassung stabilisiert Bodenanhebungen in ähnlichem Maße wie
die erste lineare Interpolation, während die Robustheit gegenüber Bodenabsenkungen größer ist, aber
kleiner als die der zweiten linearen Interpolation.
Mit den getesteten Anpassungen von $G_{\text{F}}$ können im gestörten Sprung höhere Steifigkeiten erreicht
werden (Abbildung 7). Die größte Änderung ist für die zweite lineare Anpassung in Abhängigkeit
von der Fallhöhe zu beobachten, während die erste lineare Interpolation die Steifigkeit nur geringfügig
erhöht.
Diskussion der adaptiven Einstellung der Reflexparameter
Es konnte gezeigt werden, dass eine adaptive Gainanpassung des FFB während eines jeden Sprungs den Lösungsbereich
stabiler Hüpfmuster gegenüber konstanten Feedbacks für Bodenabsenkungen erhöht. Sowohl mit den zwei linearen als auch mit dem exponentiellen Zusammenhang
zwischen $G_{\text{F}}$ und der Fallhöhe, die während der Simulation durch die Flugzeit bestimmt wird, kann eine
Vergrößerung des Stabilitätsbereichs erzielt werden. Dies geht allerdings mit einer Verringerung des
stabilen Bereichs für Bodenanhebungen einher.
Durch die exponentielle und die linearen Anpassungen des $G_{\text{F}}$ konnte bei Bodenabsenkungen, wie erwartet,
die Beinsteifigkeit erhöht werden. Da auch die Literatur eine aufgabenabhängige Gainanpassung
unterstützt (Prochazka, Gillard und Bennett,1997), ist eine Anpassung der Gains zur Erhöhung der Steifigkeit und damit ein höheres
Maß zur Dissipation der Energie denkbar, um hierdurch eine größere Stabilität zu erreichen.
Zusammenfassung und Ausblick
Basierend auf dem Modell nach Geyer (Geyer et al., 2003), wurde durch Schumacher (Schumacher und Seyfarth, 2017) eine Erweiterung zur Abmischung mehrerer Feedbacks implementiert. Dieses erweiterte Modell wurde in dieser Arbeit zusätzlich um ein zweites Bein ergänzt. Die Störuntersuchungen dieses Modells anhand der Sensor-Motor Maps haben ergeben, dass die Topologien robust gegen Veränderung der Feedbackgains, des LFB-Offset und der Bodennachgiebigkeit waren. Dagegen wurde bei Änderung der Beinlänge, des LFB-Offset oder bei Störung der Sensorsignale durch Delay und Rauschen zusätzlich die Status Stehenbleiben und Schwingen vorhergesagt.
Dies galt bei Verzögerung des VFB sowie aller Feedbacks und bei Verrauschen des LFB sowie aller Feedbacks.
Überraschenderweise wurde durch das Rauschen der ursprüngliche Instabilitätsbereich verkleinert.
Für das LFB-Offset und alle getesteten Verzögerungen der Sensorsignale wurde zusätzlich die Topologie der Performance und der anderen Untersuchungskriterien teilweise grundlegend verändert.
In dieser Arbeit wurden nur einzeln wirkende Störungen betrachtet. In weitergehenden Studien sollten Kombinationen von Störungen getestet werden, da der Mensch in seiner Umwelt auch gleichzeitig von verschiedenen Störungen umgeben ist, wie beispielsweise das Laufen auf einer Wiese (nachgiebiger Boden) mit Löchern (Bodenhöhenvariation). Hier wäre interessant, ob Störungen, die den Stabilitätsbereich vergrößern, genutzt werden können, um beispielsweise robuster auf Bodenabsenkungen zu reagieren.
Die meisten Asymmetrien zeigten grundsätzlich den halben Effekt einer symmetrischen Störung, sodass kein Einfluss durch die Asymmetrie selbst feststellbar war. Die asymmetrische Störung durch einseitige Verzögerung der Sensorssignale hingegen konnte den Stabilitätsbereich vergrößern.
Die Untersuchung der Asymmetrie sollte in zukünftigen Arbeiten erweitert werden. Merker fand lediglich für eine bestimmte Einstellung der Asymmetrie eine verbesserte Stabilität (Merker et al., 2011). In dieser Arbeit wurden jeweils nur zwei Asymmetrieeinstellungen je Störung betrachtet. Ähnlich wie die Untersuchung der Bodenhöhenstörung sollte die Asymmetrie immer weiter gesteigert und die Stabilitätsgrenzen aufgetragen werden.
Die Untersuchung der Kapazität des Modells, Störungen auszugleichen, wurde anhand von Bodenhöhenvariationen durchgeführt. Der Vergleich von effizienz- und performance-optimierten Feedbackparametern zeigte, dass erstere Feedbackeinstellung zu einer größeren Robustheit führt.
Allgemein konnte festgestellt werden, dass Feedbacks mit einer im ungestörten Fall höheren Performance weniger robust sind als solche mit einer niedrigen Hüpfhöhe.
Es blieb offen, wie es bei den Bodenanhebungen zu Unterschieden der Robustheit verschiedener Feedbackkonfigurationen kam. Weitere Untersuchungen bei Aufprägen der Störung in der Standphase, sodass das hybride System nicht von Flug- in Standphase wechselt, sollten durchgeführt werden.
Außerdem wurde die Ausregelzeit nach Störungen nicht beachtet. Zukünftige Arbeiten sollten diese berücksichtigen. Dabei stellt sich die Frage, ob besonders stabile Blendings Störungen langsamer ausregeln bzw. andere Zusammenhänge zwischen Robustheit und Performance gefunden werden können. Außerdem ist nicht untersucht, ob die Robustheit durch die Kombination mit Feedforward noch verbessert werden kann.
Zum Vergleich des menschlichen Hüpfverhaltens mit dem Modell wurden zwei Probanden betrachtet. Diese reagierten unterschiedlich auf die unerwartete Bodenhöhenstörung. Proband 1 hielt seine Beinsteifigkeit konstant, Proband 2 erhöhte seine Beinsteifigkeit im gestörten Sprung stark. Dabei war diese Verstärkung umso größer, je höher die Störung war. Entgegen diesen Beobachtungen, sagte das Modell eine verringerte Beinsteifigkeit als im ungestörten Fall voraus. Die Beinsteifigkeit wurde umso geringer, je tiefer der Boden absank. Das experimentelle Ergebnis konnte daher durch das Modell mit konstanten Feedbackparametern nicht abgebildet werden. Für eine realitätsnahe Betrachtung wird daher eine adaptive Gainanpassung notwendig.
Aufgrund der geringen Anzahl an Probanden, die stark verschiedene Störreaktionen zeigen, kann keine Aussage getroffen werden, wie der Mensch seine Beinsteifigkeit anpasst. Hierzu werden weitere experimentelle Ergebnisse benötigt.
Im letzten Teil konnte gezeigt werden, dass durch lineare Gainanpassung des FFB, die Verringerung der Steifigkeit im gestörten Sprung vermindert und damit auch die Robustheit bei Bodenabsenkungen erhöht werden konnte. Dafür wurden zwei lineare Interpolationen zwischen Gain und Fallhöhe getestet, eine mit kleinen Bodenabsenkungen als Stützstelle, die zweite mit einer kleinen und einer großen Bodenabsenkung. Beide getesteten Interpolationen konnten Bodenanhebungen nur noch im geringerem Maße stabilisieren als dies bei einer konstante Feedbackverstärkung der Fall war. Mit einer exponentiellen Regression konnten die Vorteile der beiden linearen Interpolation teilweise kombiniert werden, sodass Bodenanhebungen wie für die erste lineare Interpolation und Bodenabsenkungen im ähnlich großen Maß wie bei der zweiten Variante der linearen Interpolation stabilisiert werden konnten. Durch diese einfachen Anpassungen des Gains an die Fallhöhe bzw. Flugzeit ließ sich das menschliche Verhalten bei Bodenabsenkungen bereits besser abbilden. Abweichungen zu den experimentellen Ergebnissen bestehen aber nach wie vor.
Literatur
BLUM, Yvonne ; RUMMEL, Juergen ; SEYFARTH, Andre: Advanced swing leg control for stable locomotion.
In: Autonome Mobile Systeme 2007. Springer, 2007, S. 301–307
DALEY, Monica A. ; BIEWENER, Andrew A.: Running over rough terrain reveals limb control for
intrinsic stability. In: Proceedings of the National Academy of Sciences 103 (2006), Nr. 42, S. 15681–
15686
DONELAN, J M. ; KRAM, Rodger u. a.: Mechanical and metabolic determinants of the preferred step
width in human walking. In: Proceedings of the Royal Society of London B: Biological Sciences 268
(2001), Nr. 1480, S. 1985–1992
FARLEY, Claire T. ; MORGENROTH, David C.: Leg stiffness primarily depends on ankle stiffness during
human hopping. In: Journal of biomechanics 32 (1999), Nr. 3, S. 267–273
FERRIS, Daniel P. ; FARLEY, Claire T.: Interaction of leg stiffness and surface stiffness during human
hopping. In: Journal of applied physiology 82 (1997), Nr. 1, S. 15–22
FERRIS, Daniel P. ; LOUIE, Micky ; FARLEY, Claire T.: Running in the real world: adjusting leg stiffness
for different surfaces. In: Proceedings of the Royal Society of London B: Biological Sciences 265
(1998), Nr. 1400, S. 989–994
GEYER, Hartmut: Simple models of legged locomotion based on compliant limb behavior= Grundmodelle
pedaler Lokomotion basierend auf nachgiebigem Beinverhalten, Dissertation, 2005
GEYER, Hartmut ; SEYFARTH, Andre ; BLICKHAN, Reinhard: Positive force feedback in bouncing gaits?
In: Proceedings of the Royal Society of London B: Biological Sciences 270 (2003), Nr. 1529, S. 2173–
2183
GURNEY, Burke: Leg length discrepancy. In: Gait & posture 15 (2002), Nr. 2, S. 195–206
HÄUFLE, DFB ; GRIMMER, Sten ; SEYFARTH, Andre: The role of intrinsic muscle properties for stable
hopping–stability is achieved by the force-velocity relation. In: Bioinspiration & biomimetics 5
(2010), Nr. 1, S. 016004
HORTOBÁGYI, Tibor ; DEVITA, Paul: Muscle pre-and coactivity during downward stepping are associated
with leg stiffness in aging. In: Journal of Electromyography and Kinesiology 10 (2000), Nr. 2,
S. 117–126
KRISHNASWAMY, Pavitra ; BROWN, Emery N. ; HERR, Hugh M.: Human leg model predicts ankle
muscle-tendon morphology, state, roles and energetics in walking. In: PLoS computational biology
7 (2011), Nr. 3, S. e1001107
MCNEILL ALEXANDER, R: Energetics and optimization of human walking and running: the 2000
Raymond Pearl memorial lecture. In: American journal of human biology 14 (2002), Nr. 5, S. 641–
648
MERKER, Andreas ; KAISER, Dieter ; SEYFARTH, Andre ; HERMANN, Martin: Stable running with asymmetric
legs: A bifurcation approach. In: International Journal of Bifurcation and Chaos 25 (2015),
Nr. 11
MERKER, Andreas ; RUMMEL, Juergen ; SEYFARTH, Andre: Stable walking with asymmetric legs. In:
Bioinspiration & biomimetics 6 (2011), Nr. 4
MORITZ, Chet T. ; FARLEY, Claire T.: Passive dynamics change leg mechanics for an unexpected
surface during human hopping. In: Journal of Applied Physiology 97 (2004), Nr. 4, S. 1313–1322
MÜLLER, Roy ; BLICKHAN, Reinhard: Running on uneven ground: leg adjustments to altered ground
level. In: Human movement science 29 (2010), Nr. 4, S. 578–589
PROCHAZKA, Arthur ; ELLAWAY, Peter: Sensory systems in the control of movement. In: Comprehensive
Physiology (2012)
PROCHAZKA, Arthur ; GILLARD, Deborah ; BENNETT, David J.: Implications of positive feedback in the
control of movement. In: Journal of neurophysiology 77 (1997), Nr. 6, S. 3237–3251
SCHUMACHER, Christian ; SEYFARTH, André: Sensor-Motor Maps for describing linear reflex composition
in hopping. In: Frontiers in computational neuroscience 11 (2017)
WOLPERT, Daniel M. ; FLANAGAN, J R.: Motor prediction. In: Current biology 11 (2001), Nr. 18,
S. R729–R732