Inhaltsverzeichnis
LM 4 Anwendung
| Modul-Icon | LM 4 Anwendung des Feder-Masse-Modells |
|---|---|
| Veranstaltung | keine |
| Autor | Daniel Maykranz |
| Voraussetzung | Module LM 1-3, GM 1-2 |
| Bearbeitungsdauer | 45 min |
| Matlab Datei | Apex-Return-Map |
| Zuletzt geändert | 17.10.2013 |
Einleitung
In diesem Modul sollen die in den vorherigen Modulen vorgestellten Konzepte zusammen angewandt werden. Das mit Simulink programmierte Feder-Masse-Modell soll auf Periodizität und Stabilität untersucht und der Einfluss der Konfigurations-Parameter auf die numerische Lösung untersucht werden.
Inhalte
Apex-Return Map
Mit Hilfe der Apex-Return Map kann man anschaulich darstellen, ob und wo periodische Renn-Muster im Feder-Masse-Modell auftreten.
Um eine Apex-Return Map zu erstellen, muss in dem Simulink-Modell noch ein „to workspace“-Block eingefügt werden, der den Ortsvektor zum Zeitpunkt des Apex beinhaltet. Ausserdem wird die maximale Schrittzahl noch auf 1 gesetzt.
<imgcaption image1 | Ausgabe der Apex-Höhe in den workspace>
 </imgcaption>
</imgcaption>
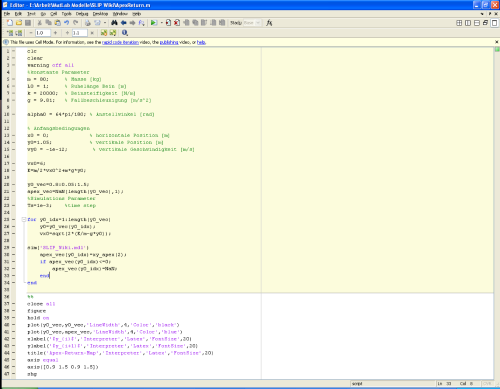
Im folgenden Beispiel ist die Apex-Return Map für das Feder-Masse-Modell für spezifische Werte für die Parameter des Modells (Masse, Beinlänge, Steifigkeit,…) in einem Matlab m-file angegeben.
<imgcaption image2 | m-file mit Apex-Return Map >
 </imgcaption>
</imgcaption>
In diesem m-file werden zuerst die Parameter (Masse, Steifigkeit, etc.) deklariert und dann das Modell mit verschiedenen Anfangsbedingungen gestartet. Wichtig dabei ist, dass die Energie für jede gewählte Anfangsbedingung identisch ist. D.h. startet das Modell aus einer größeren Höhe, ist die Geschwindigkeit niedriger. Für jede der gewählten Anfangshöhen (y0_vec) läßt man das Modell einen Schritt rennen und speichert die Apexhöhe ab (apex_vec). Stellt man nun die Apexhöhe über die Anfangshöhe dar, ergibt sich die Apex-Return Map.
<imgcaption image3 | Apex-Return Map >
 </imgcaption>
</imgcaption>
In dieser Apex-Return Map sieht man zwei Fixpunkte: ein Fixpunkt liegt bei einer Apexhöhe von 0.97 und ein Fixpunkt liegt bei einer Apex-Höhe von 1.45. Hier kann man bereits graphisch ablesen, dass der niedrige Fixpunkt stabil und der hoe instabil ist. Zur Erinnerung: ist der Anstieg im Fixpunkt betragsmäßig kleiner 1 ist der Fixpunkt stabil, ist der Anstieg im Fixpunkt betragsmäßig größer 1 ist der Fixpunkt instabil. Die Identitätslinie hat den Anstieg von 1. Der Fixpunkt bei 0.97 hat einen kleineren Anstieg als 1 und der Fixpunkt bei 1.45 hat einen Anstieg größer als 1. Je nachdem, wie die Apex-Return Map die Identitätslinie schneidet kann man somit den Stabilitätscharakter bestimmen.
Configuration Parameters
Wie gut die numerische Lösung die exakte Lösung approximiert hängt auch von der Wahl der Einstellungen des Lösungsalgorithmus ab.
In der obigen Abbildung der Apex-Return Map wurden die maximale Schrittweite (max step size) auf eine tausendstel Sekunde gesetzt. Die Parameter für den relativen und absoluten Fehler (relative und absolute tolerance) wurden auf $10^{-12}$ gesetzt.
In der folgenden Abbildung der Apex-Return Map wurden die standardmäßigen Einstellunge beibehalten (d.h. die Werte blieben auf „auto“).
<imgcaption image4 | Apex-Return Map mit standardmäßigen Einstellungen für den Lösungsalgorithmus>
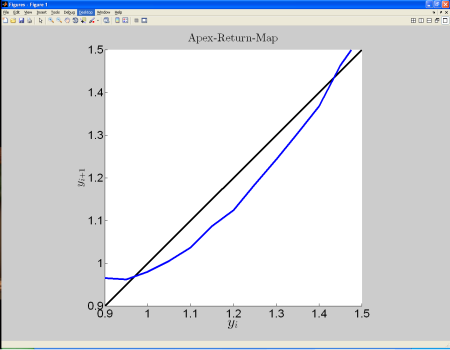 </imgcaption>
</imgcaption>
Man sieht, dass diese Apex-Return Map nicht so „glatt“ ist, wie die Erste. Wenn man den Vektor für die Anfangshöhe (y0_vec) feiner wählt (z.b. mit Abstand 0.005 statt 0.05), wird die Apex-Return Map noch „zackiger“. Die standardmäßigen Einstellungen für den Lösungsalgorithmus sind somit nicht gut geeignet für dieses Problem.
Generell sollte man skeptisch werden, wenn unerwartet Lücken, Knicke oder andere Unstetigkeiten auftauchen. In dem Fall sollte die gefundene Lösung kritisch hinterfragt werden. Eine weitere Möglichkeit ist, physikalische Erhaltungssätze (Energie-, Impuls-, Drehimpulserhaltung) zu prüfen. Das Feder-Masse-Modell ist energiekonservativ und sollte daher über den gesamten Verlauf der Simulation eine konstante Energie aufweisen. Schwankt die Energie stark, dann sollten die Einstellungen zum Lösungsalgorithmus geändert werden.
Downloads
Unter folgendem Link ist das m-file zu finden, welches die Apex-Return-Map erzeugt und ausgibt:
Fragen
- Im oben genannten Beispiel wurde der Anstellwinkel auf 64° gesetzt. Wie sieht die Apex-Return Map für einen Anstellwinkel gleich 63° und 62° aus? Was passiert mit den Fixpunkten? Wie sieht die Apex-Return Map für einen Anstellwinkel gleich 66° aus? Was passiert mit den Fixpunkten? (Stichwort: Bifurkation)
- Erweitere das Simulink-Modell des Feder-Masse-Modells so, dass die Gesamtenergie (d.h. potentielle und kinetische Energie) zum Zeitpunkt des Apex bestimmt werden kann! Überprüfe, inwiefern die Einstellungen absoluter und relativer Fehler (relative und absolute tolerance) für den Lösungsalgorithmus Auswirkung auf die Energieerhaltung haben! Vergleiche dazu die Energie zum Anfang der Simulation mit der Energie nach einem Schritt!
