Inhaltsverzeichnis
MM 1 Produktansatz
| Modul-Icon | MM 1 Umsetzung Produktansatz in Matlab |
|---|---|
| Veranstaltung | keine |
| Autor | Daniel Maykranz |
| Voraussetzung | Module MUS 3 und MUS 4, Matlab MAT 1 |
| Matlab Datei | Muskel Parameter |
| Bearbeitungsdauer | 30 min |
| Zuletzt geändert | 17.10.2013 |
Einleitung
Dieses Modul ist noch in Vorbereitung.
In diesem Modul werden verschiedene Ansätze für die Kraft-Längen-Funktion gezeigt. An einem Beispiel wird die Umsetzung und graphische Darstellung des Produktansatzes in Matlab vorgestellt.
Inhalte
Der Produktansatz für die Muskelkraft (siehe Modul MUS4 Produktansatz)
;#; $F_{M} =Act*F_{Iso} * F_l * F_v$ ;#;
für $Act=1$ kann in einem dreidimensionalen Graphen dargestellt werden indem jeweils eine Achse die Kraft-Längen- bzw. Kraft-Geschwindigkeitsrelation beinhaltet.
Ansätze für die Kraft-Längen-Funktion
Für die Kraft-Längen-Relation können verschiedene Ansätze gewählt werden. Die hier vorgestellten Ansätze haben alle gemein, dass sie bei der optimalen Faserlänge die maximale Kraft produzieren, bei Verkürzung oder Verlängerung die produzierte Kraft abfällt und bei Überschreitung des maximalen Bewegungsspielraumes die Kraft auf Null abfällt.
Parabelfunktion
Die Umsetzung der Kraft-Längen-Funktion als umgedrehte Parabel wurde bereits im Modul Produktansatz beschrieben. Dieser Ansatz hat den Vorteil, dass er mathematisch leicht zu beschreiben ist. Dieser Ansatz hat aber den Nachteil, dass die Kraft-Längen-Funktion einen Knick hat, wenn sie Null erreicht. Solche Knicke können bei der numerischen Umsetzung Probleme bereiten.
Stückweise lineare Funktion
Ebenfalls mathematisch leicht zu beschreiben ist die stückweise lineare Funktion (Siebert 2008).
;#;
$f_l&=f_c \frac{L_{cc}-L_1}{L_2-L_1} &\text{für} \: &\:L_1<L_{cc}< L_2
f_l&=\frac{f_c-1}{L_2} (L_{cc}-L_2)+f_c &\text{für} \: &\:L_2<L_{cc}<0
f_l&=1 &\text{für} \: &\:0<L_{cc}<L_3
f_l&=-\frac{1}{L_4-L_3} (L_{cc}-L_3)+1 &\text{für} \: &\:L_3<L_{cc}<L_4$
;#;
Bei diesem Ansatz wird die Kraft-Längen-Funktion in Bereiche mit verschiedenen linearen Anstiegen unterteilt. Während die linearen Bereiche leicht umzusetzen sind, können aber auch hier bei den Knicken Probleme bei einer numerischen Umsetzung auftreten.
<imgcaption image1 | Kraft-Längen-Funktion mit stückweise linearen Abschnitten>
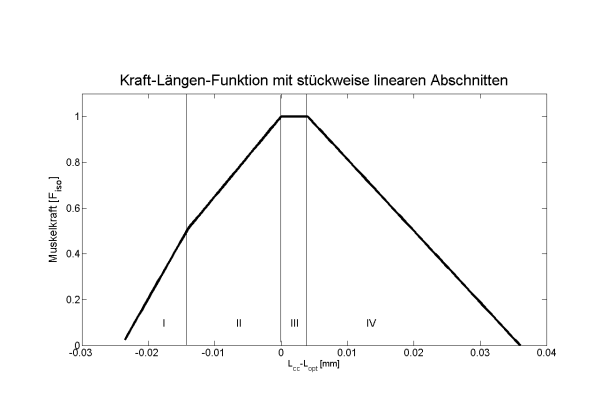 </imgcaption>
</imgcaption>
Glockenkurve
Eine etwas komplexerer Ansatz ist die Umsetzung mit Hilfe einer Exponentialfunktion (Geyer 2003).
;#; $f_l=e^{c\lvert \frac{l_{CE}-l_{opt}}{l_{opt}w}\rvert^3}$ ;#;
Dieser Ansatz hat den großen Vorteil, dass die Funktion über den gesamten Bereich glatt (also stetig differenzierbar) ist und somit keine numerischen Probleme auftreten.
<imgcaption image2 | Kraft-Längen-Funktion Glockenkurve>
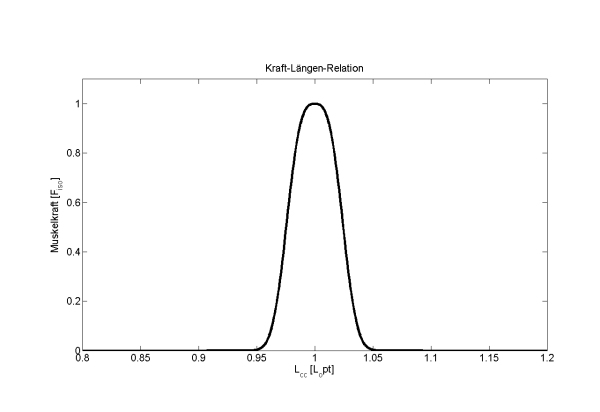 </imgcaption>
</imgcaption>
Umsetzung in Matlab
In dem hier gewählten Beispiel wird die Kraft-Längen-Relation mit einer stückweise linearen Funktion beschrieben.
<imgcaption image3 | Muskelkraft>
 </imgcaption>
</imgcaption>
Wenn man den Graphen normiert, dann sieht der Graph unabhängig von den gewählten Parametern (mit Ausnahme des Krümmungsparameters) jedesmal identisch aus. Normiert heisst in diesem Falle, dass die Achsen jeweils vielfache der maximalen Kontraktionsgeschwindigkeit $v_{max}$ bzw. isometrischen Kraft $F_{Iso}$ darstellen. Da Matlab ein numerisches Programm ist, sind jedoch Zahlenwerte für die Parameter notwendig um die Kraftrelation darstellen zu können. Im folgenden Matlab-File werden Parameter von einem Katzen-Soleus-Muskel nach Siebert (2008) genutzt. In diesem Matlab-File werden die notwendigen Parameter deklariert, der Produktansatz ausgeführt und dann graphisch dargestellt.
Zusammenfassung
Die Kraft-Längen-Funktion für den Produktansatz der Muskelkraft kann durch verschiedene Ansätze dargestellt werden. Die hier vorgestellten Kraft-Längen-Funktion haben alle die Eigenschaft, dass sie bei der optimalen Muskelfaserlänge die maximale Kraft produzieren und ausserhalb des maximalen Bewegungsspielraumes des Muskels die erzeugte Kraft auf Null abfällt. Mit der Auswahl einer geeigneten Kraft-Längen-Funktion kann der Produktansatz in Matlab durch ein m-file umgesetzt werden.
Downloads
Unter folgendem Link ist das m-file zu finden, welches den Produktansatz umsetzt und grafisch ausgibt:
Fragen
- Erstelle den dreidimensionalen Graph der Muskelkraft, bei dem die Kraft-Längen-Funktion durch eine umgedrehte Parabel der Weite 50mm modelliert wird! Benutze ansonsten die im obigen m-File angegebenen Parameter!
Literatur
- Siebert, T., Rode, C., Herzog, W., Till, O., Blickhan, R. (2008). Nonlinearities make a difference: comparison of two common Hill-type models with real muscle. Biological Cybernetics. 98:133–143
- Geyer, H., Seyfarth, A., Blickhan, R. (2003) Positive force feedback in bouncing gaits? Proc. R. Soc. Lond. B. 270:2173-2183

