Inhaltsverzeichnis
DYN7 Auftrieb & Strömung
| Modul | DYN7 Auftrieb & Strömung |
|---|---|
| Kategorie | Dynamik |
| Autor | Lauflabor.de |
| Voraussetzung | – |
| Bearbeitungsdauer | ca. 60 Minuten |
Lernziele
| Lehrveranstaltung | Lernziele |
|---|---|
| PS Biomechanik | - Versch. Auftriebsarten kennenlernen - Wo/wann treten diese auf? - Welchen Einfluss haben sie? ohne Exkurse! |
Einleitung
Bei vielen Ball- und Wurfsportarten beeinflusst die Strömungsdynamik die Flugbahn des durch die Luft fliegenden Objektes und es kommt nicht selten zur Ablenkung desselbigen oder gar zum Auftrieb.
Warum landet der Tennisball immer im Feld, sobald ich ihn andrehe?
Wie schaffe ich es, dass meine Frisbee weiter fliegt?
Wenn ihr dieses Modul durchgearbeitet habt, solltet ihr die Fragen beantworten können, denn euch wird hier das dafür benötigte Grundwissen vermittelt. Nachdem euch der statische und dynamische Auftrieb erklärt wurde, wird der wunderbare Magnuseffekt vorgestellt und außerdem der Diskus- und Speerflug genauer betrachtet.
Auftrieb
Ganz allgemein gesagt kommt es immer dann zum Auftrieb, wenn sich ein Körper in einem Medium befindet und an seiner Oberseite weniger Druck herrscht als an seiner Unterseite. Durch den Überdruck wird der Körper nach oben gedrückt bzw. aufgetrieben.
Jetzt muss man allerdings noch unterscheiden, ob sich der Körper bewegt oder ob er still steht, je nachdem handelt es sich beim Auftrieb dann um den statischen oder den dynamischen Auftrieb.
Im Folgenden werden beide erklärt.
Statischer Auftrieb
„Der statische Auftrieb entsteht durch Druckunterschiede zwischen Ober- und Unterseite des Körpers in einem Medium (Luft, Flüssigkeit). Der Auftrieb greift am Volumenmittelpunkt des Körpers an (ist nicht immer identisch mit KSP) und wirkt senkrecht nach oben. Die Größe der Auftriebskraft entspricht dem Gewicht des verdrängten Flüssigkeitsvolumens“ (Blickhan et al., 2005, S. 11). Die Formel für den statischen Auftrieb lautet:
;#; $F_A = \rho * g * V$ ;#;
$\rho$ (rho) ist die Dichte des Mediums ($Luft = 1,3 \frac{mg}{cm^{3}}$, $Wasser = 1,0 \frac{g}{cm^{3}}$)
$V$ ist das vom Körper verdrängte Volumen.
Die Schwerkraft ($m * g$) verdrängt dabei das Volumen. Die Schwerkraft setzt am KSP an, die Auftriebskraft am Volumenmittelpunkt (VM). Wenn KSP und VM nicht identisch sind (bzw. nicht senkrecht übereinander liegen), dann liegen die Wirkungslinien von Schwerkraft und Auftriebskraft parallel verschoben und es entsteht ein Drehmoment.
Beim Schwimmer links sind KSP und VM verschieden, bei ihm entsteht ein Drehmoment und die Beine sinken. Rechts hat der Schwimmer seinen VM über den KSP verlagert, indem er seine Arme lang neben seinem Kopf streckt. Er bleibt nun ruhig im Wasser liegen.
Archimedes Prinzip
Der statische Auftrieb folgt dem Archimedischen Prinzip, das wie folgt lautet: „Der Auftrieb, den ein Körper in einer Flüssigkeit oder in einem Gas erfährt, ist genauso groß wie die Gewichtskraft der Menge an Flüssigkeit oder Gas, die er verdrängt“ (Blickhan et al., 2005, S. 12).
Dynamischer Auftrieb
Der Dynamische Auftrieb wird durch Bewegung erzeugt, deshalb wird er, im Gegensatz zum statischen Auftrieb, dynamisch genannt. Durch die Geschwindigkeit und Lage (Diskus) bzw. Form (Tragfläche vom Flugzeug) die ein Körper hat, wenn er durch die Luft fliegt, entsteht eine Druckdifferenz zwischen Ober- und Unterseite. Der Druck ist an der Oberseite des Körpers geringer und er steigt auf.
Berechnen lässt er sich wie der Formwiderstand, nur statt dem Widerstandsbeiwert $c_W$ wird der Auftriebskoeffizient $c_A$ verwendet:
;#; $F = A * c_A * \frac{\rho}{2} * v^2$ ;#;
Strömungsdynamik im Sport
Die Strömungsdynamik bei Wurfgeräten nimmt großen Einfluss auf ihre Flugbahn. Unterschiedliche Wurfgeräte besitzen unterschiedliche Eigenschaften. Im Sport können diese Eigenschaften vom Sportler genutzt werden, um die Flugbahn des Balles zu Steuern (z.B. „Bananenflanke“ im Fußball) oder sie für den Gegenspieler nicht berechenbar zu machen (z.B. „Flatterball“ im Volleyball).
Magnuseffekt
Der Magnuseffekt wurde entdeckt und benannt durch den Physiker Heinrich Gustav Magnus (1802 - 1870). Dieser Effekt wird auch als Magnuskraft bezeichnet.
„Diese Kraft tritt bei vielen Sportarten auf … Eigentlich … in jeder Sportart, in der sich ein Ball um die eigene Achse dreht
und sich dabei durch Luft [oder ein anderes Medium] bewegt“ (Kröpfl, 2011, S. 105).
Durch Rotation des Körpers kann die Luft länger und schneller an einer Seite des Körpers vorbeiströmen. Dies bewirkt, laut der Theorie von Bernoulli, eine Asymmetrie und Differenz hinsichtlich des Luftdrucks an den beiden gegenüberliegenden Seiten des Balles. Auf dieser Seite (wo die Luft schneller vorbeiströmt) entsteht Unterdruck. Auf der gegenüberliegenden Seite sind Rotation und Luftströmung gegenläufig, die Luft kann den Ball auf dieser Seite also nicht so schnell umströmen, weil sie von der Rotation gebremst wird. Hier entsteht somit ein Überdruck.
Für den Magnuseffekt sind ebenso die turbulenten Wirbel um den Ball von Bedeutung. Sie führen zu zeitlichen Strömungsabrissen. Der Ball erhält dadurch einen Impuls, der ihn in die entsprechende Richtung lenkt. Die Richtung des Impulses ist Abhängig von der Drehrichtung des Balls, da die Kraft „im rechten Winkel zur Strömungsrichtung der Luft und senkrecht auf den Winkelgeschwindigkeitsvektor des Balles [wirkt]“ (Kröpfl, 2011, S.105).
Durch das Wirken der Magnuskraft wird die Flugbahn des Körpers berechenbarer und die Sportler können sie besser kontrollieren. Der Magnuseffekt wird in vielen Sportarten genutzt, z.B. Tennis, Volleyball, Tischtennis, Golf etc. Die Größe der wirkenden Magnuskraft ist dabei abhängig von der Rotationszahl (vgl. Kröpf, 2011, S. 105).
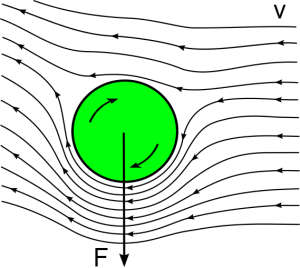
In Abbildung 3 ensteht der Unterdruck an der Unterseite des Balles, da hier die Luft den Ball länger und schneller umströmt. Der Impuls zieht den Ball nach unten.
Der Einfluss des Magnuseffekts auf die Flugbahn lässt sich berechnen (Kröpfl, 2011, S.108):
$$ \vec F_m = 1/2 * \rho * A *c_m * v * \hat \omega \times \vec v $$
mit $ \vec F_m $ = Magnuskraft, $ \hat \omega$ = Drehrichtung des Balls, $ \vec v$ = Geschwindigkeit des Balls, $ v $ = Betrag der Ballgeschwindigkeit, $ \rho $ = Luftdichte, $ A $ = Formwiderstand (hier: Querschnitt des Balls), $ c_m $ = Koeffizient des Magnuseffekts (wächst mit steigender Rotationszahl).
$ \hat \omega$ x $ \vec v$ stellt das Kreuzprodukt (oder auch Vektorprodukt) aus $ \hat \omega$ und $ \vec v$ dar, auf dessen Berechnung wir hier aber nicht eingehen.
Speerwurf
In diesem Abschnitt werden die Flugbahn eines Speers und die Kräfte, die auf diesen einwirken, aufgezeigt.
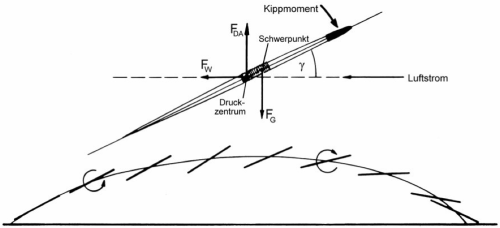
In der Flugbahn des Speers entstehen Kippmomente, da der Angriffspunkt von Auftriebs- (FDA-dynamische Auftriebskraft) und Widerstandskräfte ($F_W$) nicht gleich dem Angriffspunkt der Gewichtskraft ($F_G$) ist. Bei steigendem Angriffswinkel (y) erhöhen sich die Kippmomente. Erhält der Speer zu Beginn des Wurfes einen Drehimpuls, so ist der Angriffswinkel erhöht und der dynamische Auftrieb kann länger am Angriffspunkt greifen, somit wird der Speer weiter fliegen (vgl. Menzel, Wagner & Wank, 2009, S.284 f.).
Diskus
Beim Diskus herrschen ähnliche Bedingungen wie beim Speerwurf.
Der Diskus erhält den dynamischen Auftrieb durch das Kippmoment. Die Rotation stabilisiert den Diskus in seiner Flugbahn.

Exkurs: Strömungen
In diesem Exkurs werden verschiedene Strömungsarten, die in engem Bezug zum Sport stehen, behandelt. Ziel ist es, ein besseres Verständnis für die verschiedenen Strömungsarten zu entwickeln.
Da dies ein Exkurs ist, sind diese Inhalte nicht Kursrelevant für das PS Biomechanik.
Laminare Strömung
Es gibt zwei Fromen von Strömungen die bei Wurfgeräten entstehen, die laminare und die turbulente Strömung.
Durch flache Körper werden nur dünne Luftschichten verdrängt und können direkt hinter dem Körper wieder zusammenströmen. Dies hat nur wenig Einwirkung auf die Flugbahn des Wurfgeräts und wird laminare Strömung genannt.
Turbulente Strömung
Die turbulente Strömung entsteht bei größeren Körpern (z.B. bei einem Fußball). Hier werden mehrere Luftschichten verwirbelt, dabei entsteht hinter dem festen Körper ein Vakuum, welches eine Sogwirkung erzeugt. Die Flugbahn des Wurfgeräts wird bei einer turbulenten Strömung viel stärker beeinflusst. Bälle die die der turbulenten Strömung ausgesetzt sind, sind nicht berechenbar. Zwei bekannte Beispiele sind „Flatterbälle“ beim Volleyball oder Fußball. Für Spieler ist die Flugbahn schwer zu erkennen.
Vor dem Körper entsteht eine Grenzschicht, die sich hinter dem Ball löst und zu Verwirbelungen in der Luft führt, diese nennt man turbulente Strömungen. Dadurch entsteht hinter dem Ball ein Vakuum, das zu einem Druckwiderstand führt, der den Ball bremst. Bis zu einem kritischen Punkt steigert sich der Druckwiderstand zum Quadrat der Geschwindigkeit.
Wird dieser Punkt überschritten, löst sich die Grenzschicht vom Körper. Es bildet sich eine turbulente Grenzschicht, die zu einem verringerten Luftwiderstand führt. Auch die Luftschichten können früher wieder zusammenströmen und bilden keine turbulenten Wirbel mehr. Um so rauer die Oberfläche ist, desto schneller wird der kritische Punkt erreicht.
Exkurs: Luftwiderstand
Der Einfluss verschiedener Variablen und des Luftwiderstands auf den schrägen Wurfkönnen in diesem GeoGebra-Modell experimentell erforscht werden. Es können verschiedene Werte (Schieberegler) für die Anfangsbedingungen und Luftwiderstandsoptionen gewählt werden.
Hinweis: ein vergleichbares Modell, ohne Luftwiderstand, gibt es in KIN3
erstellt mit GeoGebra von A. Lindner
Zusammenfassung
Ihr seid am Ende des Moduls angekommen und könnt hoffentlich die Fragen aus der Einleitung beantworten. Ein kleiner Tipp: der Magnuseffekt und ein optimaler Anstellwinkel spielen eine wichtige Rolle.
Ihr habt also den statischen und dynamischen Auftrieb kennengelernt, außerdem den durch Strömung erzeugten Magnuseffekt und die Kräfte die beim Speer- und Diskuswurf wirken.
Fragen
<spoiler |1. Wann kommt es zu einem statischen Auftrieb? Wo greift die Auftriebskraft an? Wie groß ist sie?> Zu einem statischen Auftrieb kommt es durch Druckunterschiede an der Ober- und Unterseite des aufsteigenden Körpers. Die Auftriebskraft greift am Volumenmittelpunkt an. Sie lässt sich berechnen durch Multiplikation vom Volumen des Körpers (= Volumen des verdrängten Mediums), von der Dichte des Mediums (Wasser oder Luft) und von der Erdbeschleunigung g (=9.81 m/s^2). </spoiler>
<spoiler |2. Erkläre den dynamischen Auftrieb am Beispiel des Diskuswurfs im Zusammenhang mit dem Luftwiderstand!>
Wie beim Speer, erfährt der Diskus durch die nebeneinanderliegenden Angriffspunkte von Luftwiderstands-/Auftriebskraft und Gewichtskraft ein Kippmoment. Durch die Geschwindigkeit und die schräge Lage des Diskus' in der Luft, kommt es zum Druckunterschied zwischen Ober- und Unterseite und schließilch zum Auftrieb. Dynamisch heißt er in diesem Fall, weil er durch Bewegung (und nicht durch Stehen des Körpers wie beim statischen Auftrieb) erzeugt wird.
Durch den Luftwiderstand wirkt auf den Diskus eine Widerstandskraft, die ihn entgegen seiner Geschwindigkeitsrichtung abbremst, und eine Auftriebskraft, die ihn nach oben drückt. Man kann es sich ein bisschen so vorstellen, als würde der Diskus auf der Luft unter ihm 'getragen' werden oder 'schwimmen'. Der Unterschied vom dynamischen zum statischen Auftrieb ist der, dass der dynamische von der Geschwindigkeit und der Fläche senkrecht zur Strömungsrichtung abhängt und nicht von der Erdbeschleunigung und dem vom Körper verdrängten Volumen.
</spoiler>
<spoiler |3. Wann kommt es zum Magnuseffekt? Wie kann z.B. Bahnkurve eines Balles durch den Magnuseffekt verändert werden?> Zum Magnuseffekt kommt es dann, wenn sich ein runder Körper durch die Luft bewegt und sich gleichzeitig um seine Körperlängsachse dreht. Wird z.B. ein Ball angedreht geschossen, gleitet die Luft an der einen Seite schneller vorbei als an der anderen (siehe Abb.3). Auf der Seite, auf der die Luft schneller vorbeigleitet, entsteht ein Unterdruck. Der Ball wird deshalb senkrecht zur vorbeiströmenden Luft zu dieser Seite gezogen. So wird die Bahnkurve des Balles verändert. </spoiler>
Literatur
Blickhan, R., Seyfarth, A. & Wank, V. (2005). Einführung in die Biomechanik, Teil D: Äußere Kräfte, Muskel. Unveröffentlichtes Manuskript. Jena: FSU Jena.
Hahn, A. & Strass, D. (2009). Biomechanik des Schwimmens. In Gollhofer, A. & Müller, E. (Hrsg), Handbuch Sportbiomechanik (S. 364 - 389). Schorndorf: Hofmann-Verlag.
Hilgner-Recht, M. (2010). Skript GK Schwimmen. Unveröff. Manuskript. Darmstadt: TU Darmstadt.
Kröpfl, M. (2010). Physikalische Aspekte des Aufschlages beim Hallenvolleyball. Zugriff am 24.8.2013 unter:
http://physicbox.uni-graz.at/bibliothek/DA_kroepfl.pdf.
Menzel, H.-J.; Wagner, H. & Wank, V. (2009). Werfen und Stoßen. In A. Gollhofer & E. Müller (Hrsg.), Handbuch Sportbiomechanik (S. 283-316). Schorndorf: Hofmann.
Wick, D. (2009). Biomechanik im Sport - Lehrbuch der biomechanischen Grundlagen sportlicher Bewegungen (2. überarbeitete und erweiterte Auflage). Balingen: Spitta.