Inhaltsverzeichnis
KIN3 Wurf & Sprung
| Modul | KIN3 Wurf und Sprung |
|---|---|
| Kategorie | Kinematik |
| Autor | Cengic, Dahms |
| Voraussetzung | KIN1 + KIN2 |
| Bearbeitungsdauer | 60 Minuten |
| GeoGebra Datei | Schräger Wurf |
Lernziele
| Lehrveranstaltung | Lernziele |
|---|---|
| PS Biomechanik | - Unterscheidung der verschiedene Würfe/Sprünge - Eigenschaften des schrägen Wurfs |
Einleitung
Das Thema „Wurf und Sprung“ ergibt sich aus den zuvor in Kinematik I besprochenen translatorischen Größen. So ist der schräge Wurf ein Spezialfall der Translation und lässt sich in zahlreichen Sportarten beobachten, wie zum Beispiel beim Speerwurf. Eine Kombination aus freien Fall und waagerechter Wurf simuliert deren Verlauf, wie in diesem Kapitel beschrieben wird.
Freier Fall
Der freie Fall ist die Grundlage im Hinblick auf die Beschreibung des schrägen Wurfs. Sie besagt „Auf frei fallende Körper in der Nähe der Erdoberfläche wirkt als Beschleunigung die nach unten gerichtete Erdbeschleunigung“ (Tipler & Mosca, 2009, S. 79).
Diese Erdbeschleunigung wirkt mit $g = 9,81 \frac{m}{s^2}$ in vertikale Richtung (y-Achse), während in horizontale Richtung (x-Achse) keine Beschleunigung wirkt.
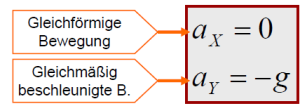
Aufgrund der konstanten Erdbeschleunigung in vertikaler Richtung handelt es sich um eine gleichmäßig beschleunigte Bewegung. Neben der konstanten Beschleunigung wird sie durch eine lineare Zunahme der Geschwindigkeit charakterisiert. Ist die Beschleunigung gleich null und damit die Geschwindigkeit konstant, wird die Bewegung als gleichförmig bezeichnet.
Weil die Erdbeschleunigung in Richtung des Erdmittelpunktes wirkt, ein Gegenstand also in Richtung des Boden beschleunigt wird, und die Höhe vom Boden aus positiv nach oben gezählt wird, ist auf das negative Vorzeichen bei $-g$ zu achten.
Ein weiterer wichtiger Aspekt ist, dass die in horizontal und vertikal gerichteten Bewegungen unabhängig voneinander sind.
Dies lässt sich anhand der Abbildung 2 verdeutlichen. Hierbei werden zwei Kugeln zeitgleich losgelassen, während die gelbe Kugel einen horizontalen Stoß zuvor erhielt. Signifikant zu sehen ist dabei, dass beide Kugeln eine gleiche vertikale Bewegung aufweisen. Damit zeigt sich, dass die vertikale Bewegung der gelben Kugel unabhängig von ihrer horizontalen Bewegung ist (vgl. Tipler & Mosca, 2009, S. 79).
Herleitung zum schrägen Wurf
Um den schrägen Wurf in seiner Flugbahn zu modellieren, werden die mathematischen Grundlagen zur Bestimmung der horizontalen und vertikalen Flugbahn benötigt. Diese Herleitung lässt sich mit Hilfe der Gesetzmäßgigkeit aus dem Kapitel Kinematik I bestimmen, welche das Verhältnis der Beschleunigung, Geschwindigkeit und des Weges über der Zeit aufzeigt. Welche Relevanz diese Gleichung im Bezug auf den schrägen Wurf hat, wird in den weiteren Kapiteln beschrieben.
Geschwindigkeit-Zeit-Gesetz
Die Beschleunigung ist durch die Erdbeschleunigung mit $a = g$ gegeben.
Diese Gleichung dient als Grundlage zur Bestimmung des Geschwindigkeit-Zeit-Gesetzes, da das Integral der Beschleunigung die Geschwindigkeit beschreibt. Somit erhalten wir aus dem Integral nach $t$ folgende Formeln:
(1)allgemein: $v = a * t$ Nun kann $a$ durch $-g$ ersetzt werden und es wird lediglich noch die Integrationskonstante $v_0$ benötigt, da diese die Anfangsgeschwindigkeit definiert.
(2)konkret: $v = -g * t + v_0$ Das ist nun die endgültige Formel des Geschwindigkeit-Zeit-Gesetzes, da $v$ nur noch in Abhängigkeit von $t$ bestimmt wird. Nun lässt sich genau bestimmen zu welchem Zeitpunkt welche Geschwindigkeit vorliegt.
Weg-Zeit-Gesetz
Dieses Gesetz lässt sich aus der Integration des Geschwindigkeits-Zeit-Gesetz bestimmen und gibt an wie viel Weg nach $t$-Zeiteinheiten zurückgelegt wurde. Dabei verläuft die Herleitung folgendermaßen:
(1)allgemein: $s = \frac{a}{2} * t^2 + v_0 * t$ Durch Integration nach der Zeit $t$ ergibt sich diese Formel. Wieder fehlt die Integrationskonstante $s_0$ bzgl. des Weges, unter dem Aspekt dass $s_0 \neq 0$ ist. Außerdem wird die Beschleunigung $a$ wieder durch den konkreten Wert $g$ ersetzt, sodass sich folgende Formel ergibt:
(2)konkret: $s = \frac{-g}{2} * t^2 + v_0 * t + s_0$ Durch Hinzufügen der Integrationskonstante beschreibt diese Gleichung das Weg-Zeit-Gesetz.
Horizontale und vertikale Bewegung
In diesem Kapitel geht es um die weitere Heranführung zur Modellierung der Flugphase beim schrägen Wurf.
Um eine Bewegung zu modellieren, beschreibt man den horizontalen und vertikalen Teil der Bewegung isoliert voneinander. Dazu teilt man sowohl die Integrationskonstante $s_0$ als auch die Geschwindigkeit $v_0$ sowie die Beschleunigung $a$ jeweils in einen $x$ und einen $y$ Anteil auf. Dadurch ergeben sich folgende Formeln zur allgemeinen Bestimmung:
(1) $x(t) = \frac{a_x}{2} * t^2 + v_{0;x} * t + x_0$
(2) $y(t) = \frac{a_y}{2} * t^2 + v_{0;y} * t + y_0$
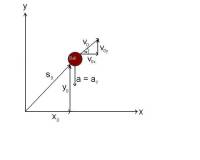
Auf der Abbildung erkennt man die Zerlegung in $x$ und $y$ daran, dass jeder diagonale Vektor durch einen vertikalen und horizontalen Vektor beschrieben wird. In der ersten Formel sind nun alle Vektoren addiert, die in x-Richtung zeigen und in der zweiten Formel sind alle Vektoren addiert, die in y-Richtung zeigen.
Um die Bewegung jetzt konkret darzustellen, werden Werte eingesetzt ($a_x = 0$,$a_y = -g$), Vorzeichen (Richtung der Vektoren) beachtet und $v_{0;x}$ und $v_{0;y}$ mit bekannten Größen beschrieben ($v_{0;x} = v_0*cos(\alpha)$, $v_{0;y} = v_0*sin(\alpha)$). Es ergeben sich schließlich folgende Formeln für das Wurf-Beispiel:
(3) $x(t) = v_0cos(\alpha) * t + x_0$
(4) $y(t) = -\frac{g}{2} * t^2 + v_0sin(\alpha) * t + y_0$
Diese beiden Bestimmungen sind Grundlage zur weiteren Bestimmung der Wurfparabel.
Der schräge Wurf
Der schräge Wurf beschreibt letztendlich zwei zueinander senkrechte Translationen (horizontal und vertikal). Durch die Anwendung dieser Formel lässt sich die Flugkurve exakt simulieren und somit aus biomechanischer Sicht die Verbesserung der Flugweite bestimmen.
Die finale Gleichung ergibt sich dabei aus dem Zusammenführen der Eigenschaften der horizontalen und vertikalen Bewegung. Hierzu wird die Formel der Horizontalen nach t umgestellt und in in die zweite Gleichung eingesetzt.
(1) $x(t) = v_0cos(\alpha) * t + x_0 \implies t = \frac{x(t)-x_0}{v_0cos(\alpha)}$
(2) $y(t) = - \frac{g}{2} * t^2 + v_0sin(\alpha) * t + y_0$
Durch das Einfügen der umgestellten ersten Gleichung in die zweite Gleichung ergibt sich die Wurfparabel, die die Flugkurve simuliert. (Hinweis: der $tan(\alpha)$ ergibt sich durch die Vereinfachung des Terms $\frac{sin(\alpha)}{cos(\alpha)}$ und man nimmt an, dass $x_0 = 0$ )
Wurfparabel: $y(t) = - \frac{g}{2 * v_0^2cos(\alpha)^2} * x(t)^2 + tan(\alpha) * x(t) + y_0$
Die folgende Abbildung soll die Zusammenhänge nochmals verdeutlichen um die Inhalte der Wurfparabel zu verstehen. Entscheidend ist es dabei zu wissen, dass die Formel die horizontale ($x(t)$) und vertikale ($y(t)$) Bewegung, sowie die Anfangsgeschwindigkeit $v_0$, Abwurfwinkel $\alpha$ und Abwurfhöhe $y_0$ berücksichtigt. Durch diese Konstellationen wird letztendlich die Flugkurve bestimmt und die Flugweite limitiert.
Beispiel beim Kugelstoßen
Beim Kugelstoßen geht es darum eine Kugel über eine Distanz möglichst weit zu stoßen. Durch das Hintergrundwissen der zuvor benannten Formeln zur Bestimmung der Wurfweite lässt sich durch biomechanische Betrachtungsweise genau definieren, wie eine Steigerung erzielt werden kann. Dabei „ist mit der Steigerung der Abwurfgeschwindigkeit ($v_0$) der größte Weitenzuwachs zu erwarten…“ (Wick, 2009, S. 208). Weiterhin ist die Abwurfhöhe und der Abwurfwinkel entscheidend, fällt aber nach Betrachtung der Gleichung weniger ins Gewicht. Dieses Wissen kann nun von den Traininern an die Athleten weiter gegeben werden, um deren Leistungen zu verbessern.
Fazit
Aufgrund der hohen Anzahl an verschiedenen Formeln ist es essentiell die Formeln und deren Nutzen zu verstehen. Nach Bearbeitung dieses Wikis sollten die Zusammenhänge des Freien Falls, des Weg-Zeit-Gesetzes, der horizontalen und vertikalen Bewegung, sowie des schrägen Wurfs bekannt sein. Letztendlich sollten auch die limitierenden Faktoren verinnerlicht sein, die die Wurfweite implizieren.
Abschließendes Beispielprogramm
Im unteren GeoGebra-Fenster ist die Flugbahn einer Kugel zu erkennen. Die Flugweite ist abhängig von den Parametern Abwurfgeschwindigkeit $v_0 [m/s]$, Abwurfwinkel $\alpha [Grad]$, und Abwurfhöhe $h [m]$. Diese Parameter können mehr oder weniger durch Training verändert werden, oder hier im Applet durch ziehen an den Schiebereglern mit der Maus. Außerdem spielt die Erdanziehung eine entscheidende Rolle. Sie zieht das Wurfobjekt in Richtung Boden (vertikale Kraft) und führt dadurch zum parabelförmigen Verlauf der Flugbahn.
Sind diese Parameter bekannt, kann man die Flugbahn (Wurfparabel) der Kugel berechnen. Durch Manipulation der Parameter können beispielsweise folgende Fragen beantwortet werden:
1. Gibt es einen optimalen Abwurfwinkel, so dass die Wurfweite maximal wird? Wenn ja, wie groß ist er?
2. Ist der optimale Winkel abhängig von der Abwurfgeschwindigkeit und / oder der Abwurfhöhe?
erstellt mit GeoGebra
Zusammengefasst in 3 Teilen
Diese Zusammenfassung deckt in jedem Fall das nötige Wissen für die Fragebögen und greift die wichtigsten Sachverhalte aus dem obigen Text auf. Diese Videoreihe ist nur optional und dient dem besseren Verständnis mathematisch komplexer Formulierungen.
Im ersten Teil wird der Zuschauer für die Thematik des schrägen Wurfs motiviert. Der zweite Teil beschäftigt sich ein wenig mehr mit den mathematischen Hintergründen, welche der Wurfparabel zugrunde liegen. Um die Wurfparabel geht es dann im 3. Teil der Videoreihe.
Fragen
<spoiler| 1.Was wird mit $g$ bezeichnet? Welchen Wert hat $g$?> $g$ steht für die Größe Erdbeschleunigung/Erdanziehungskraft. Es gilt $g = 9,81 \frac{m}{s^2}$ </spoiler>
<spoiler| 2.Wie lautet die Formel für das Weg-Zeit-Gesetz?>
Die allgemeine Formel für den Weg in Abhängigkeit von der Zeit lautet:
$s = \frac{a}{2} * t^2 + v_0 * t + s_0$.
Unterteil man die Bewegung/den Weg in einen x und einen y Anteil, ergeben sich folgende Formeln:
(1) $x(t) = \frac{a_x}{2} * t^2 + v_{0;x} * t + x_0$
(2) $y(t) = \frac{a_y}{2} * t^2 + v_{0;y} * t + y_0$
Setzt man jetzt konkrete Werte ein (Bsp. $a=-g$), beschreibt unbekannte Größen mit bekannten (Bsp.$v_{0,x} = v_0cos(\alpha)$), eliminiert $t$ aus der einen Gleichung und setzt es in die andere ein (alles ausführlich im Text beschrieben), erhält man die Gleichung für die Wurfparabel:
$y(t) = - \frac{g}{2 * v_0^2cos(\alpha)^2} * x(t)^2 + tan(\alpha) * x(t) + y_0$
</spoiler>
<spoiler| 3.Was für ein Wurf ist gegeben, wenn $v_x$ = 0 ist?> In diesem Fall handelt es sich um einen senkrechten Wurf nach oben. </spoiler>
<spoiler| 4.Was für ein Wurf ist gegeben, wenn $v_y$ = 0 ist?> In diesem Fall ist ein Wurf gegeben, der waagrecht startet und dann der ballistischen Flugbahn folgt. </spoiler>
Literatur
Seyfarth, A. (2011). Grundlagen der Biomechanik. Teil A: Kinematik. Präsentationsfolien im Rahmen des PS Biomechanik WS 2011/12. TU Darmstadt, Institut für Sportwissenschaften.
Tipler, P. & Mosca, G. (2009). Physik für Wissenschaftler und Ingenieure. Heidelberg: Springer.
Wick, D. (2009). Biomechanik im Sport: Lehrbuch der biomechanischen Grundlagen sportlicher Bewegungen. Balingen: Spitter Verlag.