Inhaltsverzeichnis
KIN1 Translation
| Modul | KIN1 Translation |
|---|---|
| Kategorie | Kinematik |
| Autor | Cengic, Tokur, Dahms |
| Voraussetzung | - |
| Weiterführende Module | GM3 |
| Bearbeitungsdauer | ca. 30 Minuten |
Lernziele
| Lehrveranstaltung | Lernziele |
|---|---|
| Vorlesung und PS Biomechanik | - translatorische Grundgrößen kennenlernen - Zusammenhang Weg-Geschwindigkeit-Beschleunigung |
| PS Forschungsmethoden 2 | - translatorische Grundgrößen kennenlernen - Zusammenhang Weg-Geschwindigkeit-Beschleunigung - Transfer zu Integration und Differentiation |
Einleitung
Alle Bewegungen von Mensch und Tier unterliegen den Gesetzen der Mechanik, dies schließt mechanische Bewegung, Ortsveränderung von Masseteilchen im Raum und Zeit ein (vgl. Hochmuth, 1967, S.7).
In diesem Modul werden die grundlegenden mechanischen Eigenschaften fortschreitender Bewegungen - von Translationen - erläutert. Dabei wird zunächst ein einführendes Beispiel gegeben, um dem Leser ein Gefühl für die Situation zu vermitteln, und dann der Begriff Translation definiert. Im Hauptteil werden die translatorischen Grundgrößen erklärt. Ein abschließendes Video stellt noch einmal die mathematischen Zusammenhänge zwischen den translatorischen Größen dar.
Einführendes Beispiel
Das folgende Video zeigt den Sprinter Usain Bolt, der die Strecke von 100m in weniger als 10s zurücklegt.
Ist es möglich, seine Geschwindigkeit bzw. Beschleunigung durch die Größen Weg und Zeit zu ermitteln?
In diesem Modul sind alle Informationen enthalten, die zur Beantwortung dieser Frage benötigt werden.
Definition
„Eine Translation liegt vor, wenn sich ein Körper so bewegt, dass die zurückgelegten Wege der einzelnen Körperpunkte zueinander parallel liegen und deckungsgleich sind. Die einfachste Translation ist danach die geradlinige Bewegung eines starren Körpers“ (Hochmuth, 1967, S.13/14).
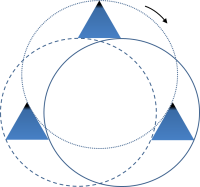
„Die Translation kann [dabei] auf einer geraden Linie [siehe Abb. 1] oder auf einer beliebig gekrümmten Kurve [siehe Abb. 2] im Raum erfolgen“ (Bräggemann, 2003, S.14).
Auch wenn es bei Abbildung 2 vielleicht erst wie eine Rotation aussieht, handelt es sich trotzdem um eine Translation. Das Dreieck dreht sich nicht, sondern wird nur verschoben. Außerdem ist, wie in der Definition erwähnt, deutlich zu erkennen, dass die zurückgelegten Wege der verschiedenen Körperpunkte deckungsgleich sind.
Nach Ballreich (1996, S. 57) beschreibt die Kinematik (hier Translation) die Bewegung eines Punktes:
„Als Beispiel kann ein Sprinter herangezogen werden, dessen Bewegungen entlang der Laufbahn an dem Körperoberflächenpunkt gemessen wird, der als erster die Lichtschranke am Ziel durchbricht. Nur für diesen Punkt gilt die Zeitangabe“.
Translatorische Grundgrößen
Die Translation kann durch die drei Größen Weg, Geschwindigkeit und Beschleunigung beschrieben werden. Diese lassen sich in einem 2-dimensionalen Koordinatensystem abbilden, das aus 2 Achsen besteht: der x-Achse (horizontal) sowie der y-Achse (vertikal); die x-Achse bildet hierbei den zeitlichen Verlauf ab.
Entscheidend ist, dass diese drei Größen in Relation zur Zeit stehen, da „alle biomechanischen Merkmale … Veränderungen mit dem Ablauf der Zeit [zeigen]“ (Ballreich & Baumann, 1996, S. 57).
Beispiele für zeitliche Merkmale können sein… (vgl. Ballreich & Baumann, 1996, S. 57)
- … die Ausführungsdauer von Bewegungen (bzw. Phasen dieser Bewegung)
- … die Zeitdauer bis zum Erreichen eines Ziels.
Folgende Tabelle gibt eine Ãœbersicht der translatorischen Größen, den dazugehörigen Symbolen sowie deren Einheiten:
| Tab.1: Biomechanische Merkmale (Ballreich & Baumann, 1996, S.57). | ||
| Bezeichnung | Symbol | Einheit |
|---|---|---|
| Zeit | $t$ | [$s$] |
| Weg | $s$ | [$m$] |
| Geschwindigkeit | $v$ | [$\frac{m}{s}$] |
| Beschleunigung | $a$ | [$\frac{m}{s^2}$] |
Weg
Der Weg (auch Strecke oder Länge) wird durch zwei Punkte im Raum festgelegt. Nach Ballreich (1996, S. 58) können die beiden Punkte entweder durch verschiedene Objekte zur selben Zeit oder ein Objekt zu verschiedenen Zeitpunkten dargestellt werden.
Beispiele hierfür sind die Messung der Körpergröße, bei der Anfangspunkt (Boden) und Endpunkt (Kopf) zum selben Zeitpunkt gemessen wird bzw. die Länge des Kugelweges beim Stoßen (Abwurf- und Landepunkt) (vgl. Ballreich, 1996, S. 58).
Bei Bewegungen ergibt der zurückgelegte Weg (z.B. Änderung der Körperposition) im Allgemeinen einen zeitlichen Verlauf (Bewegungsverlauf, auch Trajektorie genannt).
Beispiel: Ein Läufer legt innerhalb einer Minute 300m zurück. Es ist durchaus möglich, dass der Läufer während der ersten 20 Sekunden lediglich 50m zurückgelegt hat, dafür aber in den restlichen 40 Sekunden zügiger läuft und den Rest der Strecke zurücklegt.
Zu jedem Zeitpunkt erfährt man, wieviel Strecke der Läufer bereits hinter sich gelegt hat. Zudem kann ermittelt werden, wie groß die Distanz von einem Zeitpunkt zum nächsten ist.
Die Änderung des Weges innerhalb einer gewissen Zeit führt direkt zum Begriff der Geschwindigkeit:
Geschwindigkeit
Durch Differenzierung (Ableiten) des Weg-Zeit-Graphen wird ein Geschwindigkeitsverlauf erzeugt (die mathematischen Zusammenhänge werden im Video am Ende des Wikis nochmals genauer erläutert).
Die Geschwindigkeit gibt die Ortsänderung eines Punktes während eines bestimmten Zeitintervalls an (vgl. Ballreich, 1996, S. 59). Die gängige Einheit der Geschwindigkeit ist Meter pro Sekunde [m/s]. In anderen Worten: Die innerhalb einer Sekunde zurückgelegte Wegstrecke (= Ortsänderung).
Hat der Läufer keine Strecke zurückgelegt, so beträgt seine Geschwindigkeit 0 m/s. Wenn der Läufer 1 m innerhalb einer Sekunde zurückgelegt hat, so beträgt die Geschwindigkeit 1 m/s, usw.
Durch Integration (umgekehrte Ableitung) ist es möglich aus dem Geschwindigkeits-Zeit-Graphen den Weg-Zeit-Graphen bzw. aus der Geschwindigkeit den Weg zu ermitteln.
Beschleunigung
„Die Beschleunigung ist definiert als die Ableitung der Geschwindigkeit nach der Zeit“ (Ballreich & Baumann, 1996, S. 60).
Was genau heißt das?
Angenommen Usain Bolt läuft mit einer Geschwindigkeit von 20km/h. Innerhalb eines gewissen Zeitintervalls (z. B. 20s) erreicht er die Geschwindigkeit von 25 km/h. Er hat also beschleunigt (in diesem Fall die Geschwindigkeit erhöht). Bei Verminderung der Geschwindigkeit ist im Alltag die Rede von der Bremsbeschleunigung (vgl. Ballreich & Baumann, 1996, S. 61).
Die Geschwindigkeit (Ableitung des Weg-Zeit-Graphen) ist die Ortsänderung eines Punktes während der Zeit (vgl. Abschnitt Geschwindigkeit). Analog hierzu beschreibt die Beschleunigung (Ableitung des Geschwindigkeit-Zeit-Graphen) die Geschwindigkeitsänderung während der Zeit.
Ändert sich z. B. die Geschwindigkeit über einen gewissen Zeitraum nicht (z.B. 20 km/h auf einer geraden Strecke), so ist die Beschleunigung gleich Null → es hat keine Beschleunigung stattgefunden.
Durch Integration (umgekehrte Ableitung) kann aus dem Beschleunigungs-Zeit-Grafen der Geschwindigkeits-Zeit-Graphen ermittelt werden.
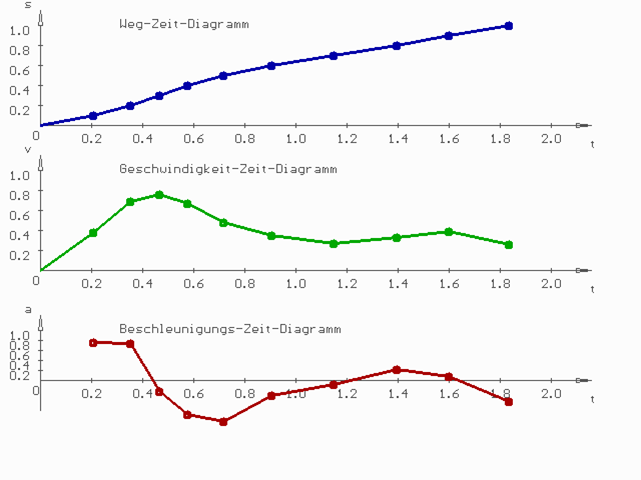
Abb. 3 zeigt einen Weg-Zeit-Verlauf (oben), Geschwindigkeitsverlauf (mitte) sowie Beschleunigungsverlauf (unten).
Exkurs: Integration & Differentiation in 5 min
Dieses Video beinhaltet eine Kurzvorstellung der Kinematik, außerdem werden mathematische Zusammenhänge (Ableitung & Integration) erläutert. Es bietet die Möglichkeit einer kleinen Auffrischung bzw. Erweiterung der persönlichen, mathematischen Kenntnisse zu dieser Thematik.
Zusammenfassung
In diesem Modul habt ihr den Begriff der Translation kennengelernt. Man nennt eine Bewegung immer dann Translation, wenn der Körper verschoben und nicht gedreht wird. Die Bewegungslinien der einzelnen Körperpunkte sind in diesem Fall parallel bzw. deckungsgleich zueinander.
Außerdem wurden euch die translatorischen Grundgrößen wie Weg, Geschwindigkeit und Beschleunigung vorgestellt. Man kann sie alle in Abhängigkeit von der Zeit beschreiben und von der einen auf die anderen schließen.
Fragen zum Modul
- Welche Größen erhält man durch einmaliges bzw. zweimaliges Differenzieren des Weg-Zeit-Graphen?
- In welcher Relation stehen die translatorischen Größen zur Zeit?
- Lässt sich von der Beschleunigung auf die Geschwindigkeit schließen? Begründe!
Antworten zu den Fragen
Antwort zu 1.: Differenziert man den Weg-Zeit-Graphen einmal, erhält man die Größe Geschwindigkeit (Änderung des Weges pro Zeiteinheit). Differenziert man den Weg-Zeit-Graphen zweimal, erhält man die Größe Beschleunigung (Änderung der Geschwindigkeit pro Zeiteinheit).
Antwort zu 2.: Alle translatorischen Größen haben eine bestimmte Beziehung zur Zeit. Der Weg gibt in Abhängigkeit von der Zeit an, an welchem Ort man sich befindet. Die Geschwindigkeit gibt in Abhängigkeit der Zeit an, wie viel Weg man in einer bestimmten Zeit zurücklegt und die Beschleunigung gibt an, wie sich die Geschwindigkeit pro Zeiteinheit ändert.
Antwort zu 3.: Ja, von der Beschleunigung lässt sich auf die Geschwindigkeit schließen. Die Beschleunigung erhält man durch einmaliges Differenzieren der Geschwindigkeit (siehe Frage 1), also kommt man von der Beschleunigung zur Geschwindigkeit durch einmaliges Integrieren (integrieren= aufleiten, differenzieren = ableiten). Hierbei ist jedoch die Anfangsbedingung v0 erforderlich.
Literatur
Ballreich, R. & Baumann, W. (1996). Grundlagen der Biomechanik des Sports. Probleme, Methoden, Modelle. Stuttgart: Enke.
Bräggemann, G.-P. (2003). Grundlagen der Biomechanik - Material zur Vorlesung. Köln: Verlag SPORT und BUCH.
Hochmuth, G. (1967). Biomechanik sportlicher Bewegungen. Frankfurt (a. M.): Limpert-Verlag GmbH.
Schüller, P. (2008). Geschwindigkeitsproblem. Zugriff am 30.07.2013 unter http://www.ammu.at/archiv/5/5_6.htm.