Inhaltsverzeichnis
GM 3 Integration in MATLAB
| Modul | GM 3 Numerische Integration in MATLAB |
|---|---|
| Veranstaltung | V Biomechanik |
| Autor | Andre Seyfarth |
| Voraussetzung | DYN1, MAT1 |
| Bearbeitungsdauer | 45 min |
| Zuletzt geändert | 24.10.2014 |
| Status | finalisiert |
Lernziele für die Lehre
Dieses Wiki wird in der Lehre angewendet. Je nach Veranstaltung sollen nach dem Erarbeiten des Wikis unterschiedliche Kenntnisse erworben werden:
| Lehrveranstaltung | Lernziel |
|---|---|
| PS Forschungsmethoden 2 | - Zusammenhang der kinematischen Grundgrößen (Weg, Geschwindigkeit, Beschleunigung) mit Bezug auf Differentiation und Integration - Was ist eine numerische Integration? - Unterschied inverses und vorwärts Modell - Kapitel Umsetzung in Matlab ist nicht relevant |
- Die Messdaten können hier herunter geladen werden.
- Das Programm zur Berechnung der KSP Bewegung kann hier herunter geladen werden.
Einleitung
In diesem Modul wird ein Vorgehen beschrieben, wie aus der Vorgabe von Kräften die resultierende Bewegung durch zweifache Integration numerisch berechnet werden kann. Grundlage hierfür sind das zweite Newtonsche Axiom ($F=m*a$) sowie der Zusammenhang zwischen den kinematischen Größen Beschleunigung $a$, Geschwindigkeit $v$ und Weg $s$.
Mit dem hier vorgestellten Rüstzeug können einfache aber auch komplexe Bewegungen auf Grundlage der Bewegungsgleichung(en) des Systems numerisch berechnet werden. D.h. es kann bestimmt werden wie sich der Zusammenhang zwischen den kinematischen Größen und der Zeit darstellt.
Einführendes Beispiel
Wir stellen uns folgende Situation vor: Ein Proband springt auf einer Kraftmessplatte (Abb. 1), welche die Bodenreaktionskräfte am Boden erfasst. Ziel ist es nun, den zeitlichen Verlauf der Höhe, die vertikale Geschwindigkeit und die vertikale Beschleunigung des Körperschwerpunktes (KSP) zu bestimmen. Hierfür wird das Verfahren der numerischen Integration verwendet.
Kinematik und Dynamik
Hierfür suchen wir zunächst den Zusammenhang zwischen Kräften im Körper zu den zugehörigen kinematischen Größen (Lage, Geschwindigkeit, Beschleunigung). Dabei wirken nach dem 2. Newtonschen Axiom die Kräfte $F$ (und Drehmomente) als Ursache von Beschleunigungen $a$ (und Winkelbeschleunigungen) mit $$F = m * a$$
Greift an einem Körper eine konstante Kraft $F$ an, so ruft diese eine gleichmäßig beschleunigte Bewegung hervor, wobei die Beschleunigung $a$ zu der Kraft $F$ proportional ist. $F$ hat hierbei die Einheit Newton ($N$) mit $ 1N = 1 \frac{kg*m}{s^2}$ . Die Einheit der Masse $m$ ist $kg$. Die Masse $m$ kennzeichnet die Eigenschaft eines Körpers, sich der Änderung seines Bewegungszustandes zu widersetzen. Sie ist ein Maß für die Trägheit des Körpers und verkörpert somit den Proportionalitätsfaktor in der oben genannten Relation.
Im Gegensatz zur Kinematik, welche die räumliche Anordnung von Körpern im Verlauf der Zeit beschreibt, berücksichtigt die Dynamik zusätzlich die mechanischen Eigenschaften von Körpern, welche durch z.B. Masse (Massenträgheitsmoment), Energie und Impuls (Drehimpuls) beschrieben werden.
Zusammenhang zwischen kinematischen Größen
Die kinematischen Größen Weg $s$, Geschwindigkeit $v$ und Beschleunigung $a$ stehen miteinander durch Differenzieren (Ableiten) und Integrieren in Beziehung. Zum Beispiel berechnet sich die Geschwindigkeit $v$ als Ableitung des Weges $s$ nach der Zeit $t$. Analog ist die Beschleunigung $a$ die Ableitung der Geschwindigkeit $v$ nach der Zeit $t$. In umgekehrter Richtung kann der Weg $s$ durch Integration der Geschwindigkeit $v$ nach der Zeit $t$ bestimmt werden. Hierfür muss zusätzlich noch der Anfangsweg $s_0$ gegeben sein, da bei der Integration nur die Änderung des Weges durch die Geschwindigkeit ermittelt wird. Analog ist berechnet sich Geschwindigkeit $v$ aus der Integration der Beschleunigung $a(t)$ über die Zeit. Auch hier muss wieder die Anfangsgeschwindigkeit $v_0$ mit berücksichtigt werden. Man nennt diesen Anfangswert $v_0$ auch Integrationskonstante.
<imgcaption image2 | Zusammenhang zwischen den kinematischen Größen. >
 </imgcaption>
</imgcaption>
Bewegungsmodelle
Mit Bewegungsmodellen können verschiedene Ansätze verfolgt werden. Zum Bespiel kann die Bewegung des Körpers kinematisch und dynamisch erfasst werden, d.h. es werden die Segmentbewegungen und externen Kräfte am Körper gemessen. Aus diesen Messdaten können nun im Körper wirkende interne Kräfte und Drehmomente (zurück) berechnet werden. Dieser Ansatz wird Inverse Modellierung (inverse dynamics model, Winter 2009) genannt werden, da praktisch die Zeit zurück gerechnet wird und aus der Beobachtung auf die Ursache der Bewegung (die im Körper wirkenden Kräfte und Drehmomente) geschlossen wird. Dieses Verfahren wird häufig in der klinischen Ganganalyse verwendet, um z.B. Defizite der Muskelfunktion auf Gelenkebene zu identifizieren.
<imgcaption image3 | Arten von Bewegungsmodellen. >
 </imgcaption>
</imgcaption>
Der hier im Mittelpunkt stehende Ansatz der Vorwärtsdynamischen Modellierung benötigt hingegen Annahmen über die auf den Körper wirkenden Kräfte und berechnet daraus die Bewegungskinematik. Häufig werden über Muskelmodelle Gelenkmomente berechnet, aus denen dann die Bewegung der Segmentkette bei gegebenen Anfangsbedingungen (Lage, Geschwindigkeit der Segmente) berechnet wird. Ein verbreitetes Werkzeug zur Berechnung von vorwärtsdynamischen Modellen ist OpenSIM (Delp et al., 2007).
Vorwärtsmodell zur Körperschwerpunkt (KSP) Berechnung
Wir wollen nun das Verfahren der vorwärtsdynamischen Modellierung an einem einfachen, in MATLAB programmierten Beispiel beschreiben. Ein Sportler führt vertikale Sprünge auf einer Kraftmessplatte aus. Diese misst die Bodenreaktionskräfte (BRK) während der Bodenkontakt in den 3 Raumrichtungen. Für unser Modell werden wir nur die vertikale Komponenten der BRK $F_y(t)$ betrachten, ein analogen Vorgehen ist für die beiden horizontalen Richtungen möglich.
<imgcaption image4 | Integration der Bodenreaktionskraft (BRK) zur Bestimmung der KSP Bewegung. >
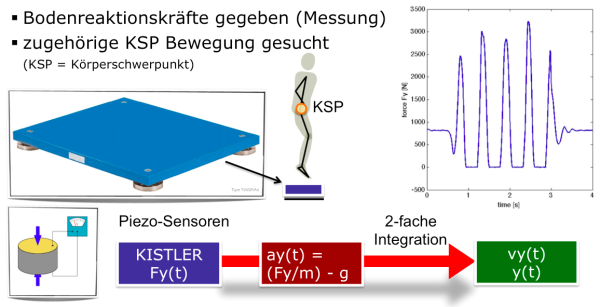 </imgcaption>
</imgcaption>
Das Vorgehen gliedert sich in folgende Schritte:
- Zunächst wird aus der vertikalen BRK $F_y(t)$ die vertikale Beschleunigung $a_y(t)$ bestimmt. Hierfür wird die Masse des Probanden sowie die Erdbeschleunigung ($g=9.81 \frac{m}{s^2}$) benötigt.
- Aus der vertikalen Beschleunigung kann nun durch zweifache Integration zunächst die vertikale Geschwindigkeit $v_y(t)$ und dann die Höhe $y(t)$ des KSP bestimmt werden. Hierfür müssen geeignete Anfangsbedingungen bestimmt werden.
Das damit anvisierte Ergebnis der Berechnung ist in der folgenden Grafik dargestellt:
<imgcaption image5 | Berechnung der KSP Kinematik (rechts) aus der BRK (links). >
 </imgcaption>
</imgcaption>
Numerische Integration
Wir setzen die Anfangsbedingungen im Stand auf $v_{y;0} = 0\frac{m}{s}$ und $y_0 = 1 m$. Jetzt können wir mit der Programmierung der ersten Integration von der Beschleunigung $a_y(t)$ über der Zeit beginnen. Das Ergebnis ist die Geschwindigkeit $v_y(t)$. Die Integration wird in Zeitschritten von $1 ms$ ($dt = 0.001 s$) durchgeführt.
<imgcaption image6 | Die numerische Integration der KSP Beschleunigung ay(i) über der Zeit (i=Index der Zeit in ms) ergibt die Geschwindigkeit vy(i). >
 </imgcaption>
</imgcaption>
Bei der Integrationsschleife in MATLAB wird für jeden Zeitschritt $i$ der nächste Wert der Geschwindigkeit $v_y(i)$ basierend auf dem Vorwort $v_y(i-1)$ plus dem Produkt von Beschleunigung $a_y(i)$ mal Zeitschritt $dt$ (hier $1 ms$) berechnet. Das ist die einfachste Form der numerischen Integration der Beschleunigung nach der Zeit mit dem Ergebnis, den entsprechenden Geschwindigkeits-Zeit-Verlauf zu erhalten.
Umsetzung in MATLAB
Die numerische Integration soll nun in MATLAB zweifach ausgeführt werden, um zunächst die vertikale Geschwindigkeit $v_y(t)$ und anschließend die Höhe des KSP $y(t)$ zu berechnen. Wir werden jetzt die notwendigen Schritte (1) zum Einlesen der Kratmessdaten, (2) zur Auswahl des Zeitfensters, (3) zur Darstellung der Kraftdaten, (4) zur Bestimmung der vertikalen Beschleunigung, sowie (5) zur zweifachen Integration für KSP Geschwindigkeit und Höhe vorstellen.
<imgcaption image7 | Matlab Programmteil zum Einlesen der Kraftdaten (Messfrequenz 1000Hz) und Auswahl des Zeitfensters von 4s bis 8s. >
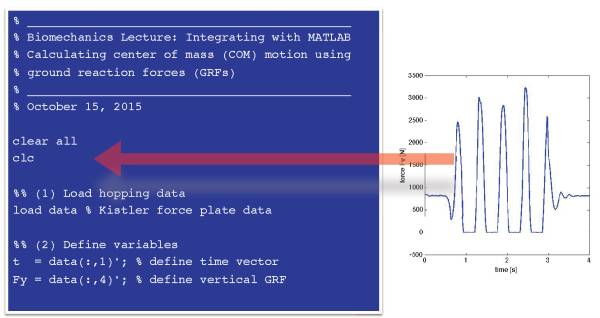 </imgcaption>
</imgcaption>
Die Messdaten (Download siehe unten) wurden in einem Textformat exportiert. Dabei liegen die verschiedenen Informationen (Zeit, Kraftkanäle) in Spalten vor, die Zeilen entsprechen den Messzeitpunkten. Der Zeitbereich ($4 s$ bis $8 s$) wird über den Vektor $sel$ ausgewählt.
<imgcaption image8 | Matlab Programmteil zum Anzeigen der Kraftdaten und zur Berechnung der vertikalen KSP Beschleunigung. >
 </imgcaption>
</imgcaption>
Die Darstellung von Zahlenreihen (Vektoren) als x-y-Diagramm in Matlab erfolgt it dem $plot(x,y)$ Befehl. Mit der Eigenschaft 'linewidth' kann die Liniendicke eingestellt werden (hier doppelte Liniendicke). Mit dem Befehl $subplot(121)$ wird das Fenster in zwei horizontal angeordnete Diagramme eingeteilt und das linke Diagram ausgewählt. Der Befehl $subplot(122)$ wählt weiter unten das rechte Diagramm aus.
Für die Bestimmung der vertikalen KSP Beschleunigung wird noch die Masse des Probanden über die mittlere vertikale Bodenreaktionskraft $mean (F_y)$ geteilt durch die Erdbeschleunigung $g$ bestimmt.
<imgcaption image8 | Matlab Programmteil zur Berechnung der vertikalen KSP Geschwindigkeit und KSP Höhe sowie zur Darstellung von Beschleunigung, Geschwindigkeit und Höhe des KSP. >
 </imgcaption>
</imgcaption>
Die zweifache Integration bestimmt vertikale Geschwindigkeit $v_y(t)$ und Höhe $y(t)$ des KSP nach dem oben beschriebenen Prinzip. Als Anfangsbedingungen (Integrationskonstanten, siehe oben) wurde hier für den aufrechten Stand eine Anfangshöhe $y_0=1 m$ und Anfangsgeschwindigkeit $v_{y;0}=0\frac{m}{s}$ gewählt.
In der Darstellung der KSP-Kinematik werden vertikale Beschleunigung, Geschwindigkeit und Höhe in einem zweiten Diagramm (rechts) dargestellt. Mit dem Befehl $legend('ay','vy','y')$ wird eine Legende im Diagramm angezeigt, um die verschiedenen Kurven besser unterscheiden zu können. Die Achsenbeschriftung erfolgt mit den beiden Befehlen $xlabel$ und $ylabel$. Der Befehl $shg$ stellt sicher, dass die Figure in Matlab gezeigt wird (falls das Fenster z.B. im Hintergrund liegt).
Zusammenfassung
Mit Hilfe der numerischen Integration kann die Bewegungskinematik aus den wirkenden Kräften abgeleitet werden. Wir haben dies am Beispiel von vertikalen Sprüngen veranschaulicht und ein entsprechendes MATLAB Programm zur Berechnung der Kinematik (Beschleunigung, Geschwindigkeit, Lage) des KSP entwickelt. In komplexeren Muskel-Skelett-Modellen kann in ähnlicher Art die Bewegung der Segmentkette als Folge der wirkenden Gelenkmomente sowie der Randbedingungen (z.B. Bodenkontakt) abgeleitet werden. Weiterführende Informationen finden sich im Kapitel 6 des Buches von David A. Winter (Winter, 20009).
Tutorials
Fragen
- Wie kann auf einer Kraftmessplatte die Masse eines Probanden bestimmt werden? Entwerfe einen Versuchsplan!
- Fasse zusammen, welche Informationen für beide Modellierungsansätze jeweils vorgegeben werden müssen und welche Aussagen gewonnen mit der Modellierung jeweils werden können.
- Nenne je ein Beispiel für die Anwendung der inversen Modellierung bzw. der vorwärtsdynamischen Modellierung!
- Für welche Art der Modellierung wird eine numerische Integration benötigt?
- Wie könnte aus der Bodenreaktionskraft und der abgeleiteten KSP Kinematik eine Aussage über die Beinsteifigkeit ermittelt werden? (Steifigkeit = Verhältnis von Kraft zur Auslenkung einer elastischen Struktur, z.B. einer Schraubenfeder.)
Literatur
- Delp, S. L., Anderson, F. C., Arnold, A. S., Loan, P., Habib, A., John, C. T., … & Thelen, D. G. (2007). OpenSim: open-source software to create and analyze dynamic simulations of movement. Biomedical Engineering, IEEE Transactions on, 54(11), 1940-1950.
- Winter, D. A. (2009). Biomechanics and motor control of human movement. John Wiley & Sons. (Informationen zur Kinematik- und Kraftmessung sowie zum Verfahren der inversen Dynamik)

