Inhaltsverzeichnis
MMB 2A Kraftdatenanalyse
| Modul | MMB 2A Kraftdatenanalyse |
|---|---|
| Kategorie | Messmethoden Biomechanik |
| Autor | Andre Seyfarth, Dario Tokur |
| Voraussetzung | Grundlagen Biomechanik |
| Bearbeitungsdauer | ca. 30 Minuten |
| Letzte Änderung | 8. Juni 2017 |
| Status | in Bearbeitung |
| Lehrveranstaltung | Lernziel |
|---|---|
| S Messwertaufnahme und -verarbeitung | - Wie werden Kraftdaten analysiert? - Wie können Bodenkontakte ermittelt werden? - Wie berechnet man die Stand- und Flugzeiten beim Sprung? - Wie berechnet man die Sprunghöhe? |
| PS Forschungsmethoden 2 | - Welche Schritte sind für die Auswertung von Kraftdaten zur Berechnung des Kraftstoßes bzw. der Sprunghöhe notwendig? |
Einleitung
In diesem Wiki wird erklärt, wie Kraftdaten aus einer Messung mit KISTLER-Kraftplatten importiert, aufbereitet und bezüglich der Kontakt und Flugzeiten analysiert werden können. Darüber hinaus wird eine Berechnung des Kraftstoßes im Bodenkontakt und der Sprunghöhe durchgeführt. Beispielhaft wird das Vorgehen für die Analyse eines Niedersprungs (drop jump) erläutert.
Kraftdaten einlesen
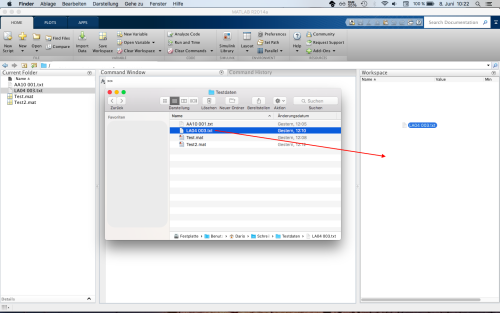
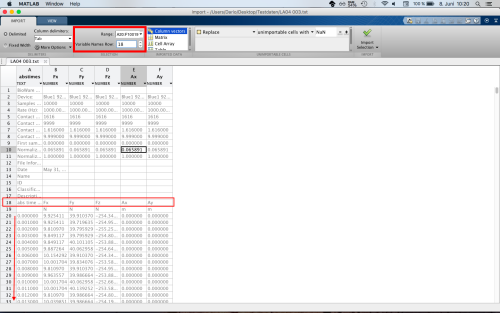
Die KISTLER Kraftdaten werden in MATLAB importiert, indem die Datei (Endung *.txt) in den Workspace von MATLAB gezogen werden (Fig.1, Drag and Drop). Danach wird der Bereich der Messwerte ausgewählt (z.B. Fig.2, ab Zeile 20, Auswahl der Spalten z.B. für Fx, Fy und Fz). Zusätzlich muss noch die Zeile mit den Variablennamen markiert werden (z.B. Fx, Fy und Fz).
Messfehler (Offset, Schwingungen) beseitigen
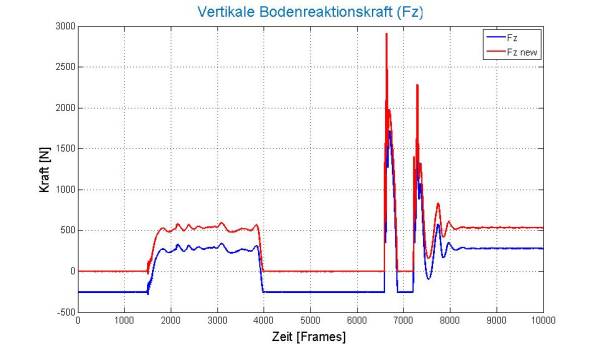
Häufig treten bei Messungen sogenannte Messfehler auf. Z.B. könnte die Kraft in der Flugphase (oder vor Betreten der Kraftmessplatte) ungleich 0 sein. Diese fehlerhafte Verschiebung der Kraft (ohne Belastung der Platte) wird als offset bezeichnet (Fig.3).
Angenommen in der vertikalen Kraft ist im Bereich der Zeitschritte von 1 bis 1000 (erste 1s bei 1000Hz Messfrequenz) der Messwert der Kraft ungleich 0:
F_offset = mean(Fz(1:1000));
Dann sollte dieser Mittelwert F_offset vom Kraftsignal abgezogen werden
Fz_new = Fz - F_offset;
Damit sind die Kraftwerte nun richtig kalibriert, d.h. die Werte werden ohne Kontakt etwa den Wert 0 haben.
Ein weiterer Messfehler könnte die Eigenschwingung der Messplatte sein (z.B. wenn die Platte nicht fest im Boden verankert ist). Dann sind die Kraftkurven von fehlerhaften Oszillationen überlagert. Um diese zu Beseitigen empfiehlt sich der Einsatz eines Filters. Ein sehr einfacher Filter ist der gleitende Mittelwert über ein Fenster von w Messwerten (z.B. w=15), d.h. der Messwert zum Zeitschritt n wird aus Mittelwert der ursprünglichen Messwerte n-7 bis n+7 berechnet:
Fz_filt = Fz_new;
w = 15; %Breite des Filterfensters, bitte ungerade Zahl benutzen
w2 = (w-1)/2; %Anzahl der Werte unterhalb/überhalb des aktuellen Zeitschrittes n
for n = 1+w2:length(Fz_new)-w2;
Fz_filt(n) = mean(Fz_new(n-w2:n+w2));
end
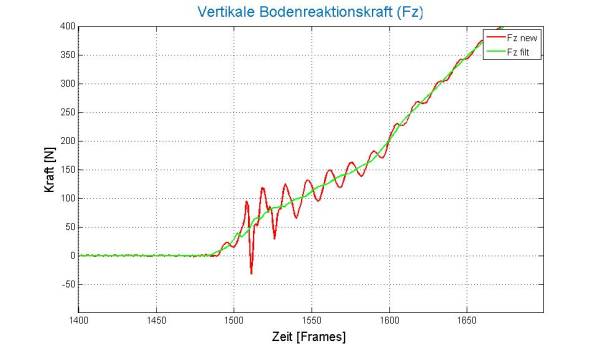
Damit sind nun die hochfrequenten Schwingungen im gefilterten Messsignal Fz_filt verschwunden (Fig.4).
<spoiler| Wie groß muss das Fenster (d.h. die Breite w) gewählt werden, um ausreichend aber nicht zu stark zu glätten?>
Die Breite des Glättungsfensters sollte entsprechend der Oszillationsfrequenz gewählt werden.
</spoiler>
Kontakte bestimmen
Nach der Beseitigung der Messfehler (z.B. Offset, Schwingungen) können die Phasen des Bodenkontakts und damit die Ereignisse Landung (TD) touch-down und Abflug (TO) take-off bestimmt werden.
Hierfür legen wir eine Schwelle (threshold) fest, ab der ein Bodenkontakt angenommen werden kann:
threshold = 20 % Schwelle 20N
Der Bodenkontakt ist dann gegeben, wenn die vertikale Kraft diese Schwelle überschreitet:
contact = (Fz_filt>threshold);
Hieraus erhält man eine Kurve (Fig.5, rote Linie), die den Wert 1 annimmt, wenn Bodenkontakt besteht und den Wert 0, wenn nicht.
<spoiler | Frage: Wie könnte der Ablauf der Messung für diesen DropJump ausgesehen haben?>
- Proband (PB) steht neben der Kraftmessplatte (KMP)
- PB stellt sich auf die KMP
- PB steigt auf das Podest und lässt sich auf KMP fallen
- PB landet auf KMP und springt ab
- PB befindet sich im Flug
- PB landet wieder auf KMP und bleibt bis zu Ende der Messunge ruhig stehen.
</spoiler>
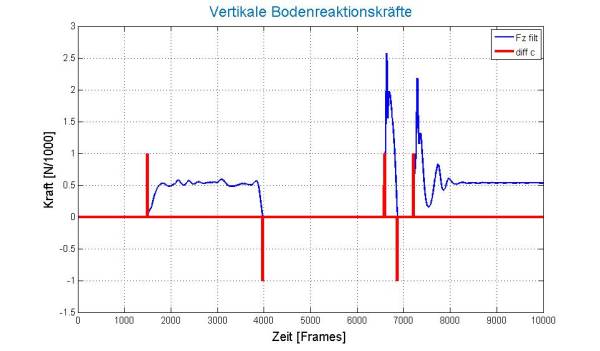
Die Zeitpunkte von Landung (bzw. Abflug) sind definiert, wenn der Wert von contact von 0 auf 1 (bzw. von 1 auf 0) wechselt. Das lässt sich einfach prüfen mit der Funktion diff, welche jeweils 2 aufeinanderfolgende Werte voneinander abzieht (Fig.6):
diff_c = diff(contact);
Dieses Differenzen-Signal ist immer 1 wenn eine Landung (TD) bzw. -1 wenn ein Abflug (TO) vorliegt. Die Zeitpunkte der Landung und des Abfluges sind dann
t_TD = find(diff_c==1); t_TO = find(diff_c==-1);
Unter Kenntnis der Messfrequenz (z.B. f=1000Hz) und dem daraus resultierenden Zeitschritt zwischen zwei aufeinanderfolgenden Messwerten (z.B. dt=1/f=0.001s) lässt sich dann die Kontakt und Flugzeit berechnen:
t_Contact = (t_TO-t_TD)*dt; t_Flight = (t_TD-t_TO)*dt;
Hierbei ist darauf zu achten, dass die richtigen TD und TO Ereignisse aus dem Vektor ausgewählt werden. Das kann am besten über eine Visualisierung des Kraftverlaufs mit einzeichnen der TD und TO Ereignisse abgelesen werden.
Kraftstoß und Sprunghöhe
Mit der Kenntnis der Zeitpunkte von Landung und Absprung kann nun der Kraftstoß S sowie die Sprunghöhe h berechnet werden.
Der Kraftstoß ist definiert durch das Integral unter der Kraft-Zeit-Kurve im Zeitfenster von Landung (TD) bis Absprung (TO). Das Integral kann berechnet werden durch die Summation der Flächen unter der Kraft-Zeit-Kurve für jeden einzelnen Zeitschritt delta_t (z.B. 0.001s) von TD bis TO:
delta_t=0.001; %Zeitschritt 1ms (Messfrequenz f=1000Hz) t_TD=TD(2); %Beginn Bodenkontakt auswählen t_TO=TO(2); %Ende Bodenkontakt auswählen S=sum(Fz(t_TD:t_TO))*delta_t; %Summe der Teilflächen Fz(n)*delta_t für n=t_TD bis t_TO
Frage: Wie kann mit dem Kraftstoß S die Änderung der Körperschwerpunkt(KSP)-Geschwindigkeit bestimmt werden?
Die Berechnung der Sprunghöhe kann mithilfe der Flugzeit erfolgen. Es gilt s = g/2 * t^2. Die maximale Sprunghöhe wird in etwa bei der halben Flugzeit erreicht:
g=9.81; % Gravitationsbeschleunigung in m/s^2 t=(TD(3)-TO(2))/2; % halbe Flugzeit h=g/2 * t^2; % Sprunghöhe
Zusammenfassung
Mit dieser Einführung in die Auswertung von Kraftsignalen können die Lande- und Abflugzeiten bestimmt werden. Damit werden weitergehende Analysen ermöglicht, z.B. die Berechnung des Kraftstoßes und der Sprunghöhe aus den Kraftdaten. Ebenso können aus der Integration der Kräfte unter Berücksichtigung der Anfangsbedingungen auch die kinematischen Daten (Weg, Geschwindigkeit) des Körperschwerpunkts berechnet werden (siehe KiN3).
Fragen
- Wie könnte man die Bestimmung der Sprunghöhe noch verbessern? Hinweis: Die vertikale KSP Bahn
y(t)berechnet sich durch zweifache Integration der Beschleunigunga_y(t). Welche Informationen werden für die Berechnung noch benötigt? - Wie könnte man die Sprungleistung (Sprunghöhe
h) bei Probanden mit unterschiedlichen Körpereigenschaften (Körpermassem_body, Körperhöheh_body) vergleichen? - Wie könnte man den Kraftstoß
Sbei Probanden mit unterschiedlichen Körpereigenschaften (Körpermassem_body, Körperhöheh_body) vergleichen?