Inhaltsverzeichnis
MMB2 Kraftmessung
| Modul | MMB2 Kraftmessung |
|---|---|
| Kategorie | Messmethoden Biomechanik |
| Autor | Filip Cengic |
| Voraussetzung | Grundlagen Biomechanik |
| Bearbeitungsdauer | ca. 45 Minuten |
| Letzte Änderung | 20. Dez 2014 |
| Status | in Bearbeitung |
| Lehrveranstaltung | Lernziel |
|---|---|
| PS Forschungsmethoden 2 | - Was ist Dynamometrie und was misst sie? - Welche Methoden gibt es? - Was bedeuten Kraftangriffspunkt und -vektor? Welchen Mehrwert für die Wissenschaft wird erzielt? |
Einleitung
Unter Dynamometrie versteht man die Messung, Analyse und Darstellung dynamischer Merkmale bei Haltungen und Bewegungen (Schwameder, 2009, S. 104).
Im aufrechten Stand wirkt die Gewichtskraft gegen den Boden. Andererseits wirkt die Kraft des Bodens gegen den Körper (→ 3. Newton'sches Axiom), welche als Bodenreaktionskraft bezeichnet wird. Aus mechanischer Sicht können Kräfte zwei unterschiedliche Wirkungen hervorrufen, nämlich Beschleunigung und Verformung. Eine beschleunigende Wirkung hat zur Folge, dass sich die Geschwindigkeit des Objekts ändert. Die verformende Wirkung der Kraft verursacht Deformationen des Körpers (Schwameder, 2009, S. 104f.).
Kraftaufnehmer
Das 3. Newton'sche Axiom bildet die Grundlage jeder Kraftmessung. Kraft tritt nie isoliert auf, sondern immer in Verbindung mit einer gleich großen Gegenkraft. In den häufigsten Fällen beruhen Kraftmessungen im Anwendungsfeld des Sports auf dem Prinzip der Deformation eines Messfühlers (direkte Messung). Eine wesentliche Voraussetzung ist die Proportionalität zwischen Kraftwirkung und Durchbiegung des elastischen Messfühlers (Wick, 2009, S. 142).
Winter (2009, S. 117) benennt vier Arten von Messfühlern:
- Piezo-elektrisch / piezo-resistiv
- Dehnungsmessstreifen (DMS)
- Kapazitiv
Dehnungsmessstreifen
Wenn externe Kräfte auf ein stationäres Objekt wirken, kommt es zur Spannung bzw. Dehnung des Objekts. Spannung ist definiert durch die internen Widerstandskräfte des Objekts. Von Dehnung ($\epsilon$) spricht man bei einer Verformung des Objekts:
;#; $\epsilon = \frac{\Delta L}{L}$. ;#;
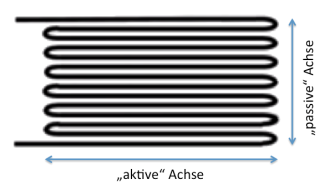
Grundsätzlich beruhen alle Dehnungsmessstreifen (DMS) auf dem Prinzip der Umwandlung von mechanischer Bewegung in ein elektrisches Signal. In einem DMS (s. Abb. 1) wird eine kalibrierte Metallplatte (oder ein Metallbalken) in einer Richtung gedehnt. Diese mechanische Verformung beträgt nur ein Bruchteil eines Prozentes und führt zu einer Änderung des elektrischen Widerstandes (Seyfarth, 2012, S. 79). Die Änderung des Widerstands steht in linearem Verhältnis zur Verformung.
Die Formel für den Dehnwiderstand $R$ ist gegeben durch
;#; $R\ =\ \frac{\rho\ L}{A}$. ;#;
Der griechische Buchstabe $\rho$ steht für den Widerstand des Drahtes, $L$ bezeichnet die Drahtlänge und $A$ die Querschnittsfläche. Wird der Metalldraht unter Spannung gehalten, verlängert dieser sich und seine Querschnittsfläche $A$ wird verringert. Der Widerstand ändert ($\Delta R$) sich in Abhängigkeit zur Dehnungsempfindlichkeit $G_f$ des Drahtes.
;#; $G_f = \frac{\frac{\Delta R}{R}}{\epsilon}$ ;#;
<spoiler|Nennen Sie mind. zwei Anwendungsgebiete für die Messung mit DMS>
Anwendungsgebiete
Dehnungsmessstreifen können im Turnsport als Reckdynamometer zur Messung der horizontalen und vertikalen bzw. der radialen und tangentialen Komponente der vom Körper auf die Reckstange ausgeübten Kräfte, eingesetzt werden. Eine weitere Einsatzmöglichkeit wäre das Skidynamometer zur Messung der zwischen Schuh und Ski auftretenden Reaktionskräfte- und -momente (Baumann, 1985, S. 167).
</spoiler>
Piezo-Sensoren
In der Mitte der 1950er Jahre entdeckten Wissenschaftler in den Bell Laboratories die piezoresistiven Eigenschaften von Germanium und Silizium. Obwohl die Materialien erhebliche Nichtlinearitäten und eine hohe Temperaturempfindlichkeit aufwiesen, war der Gage-Faktor ($G_f$) 50-mal größer, als beim Metalldraht oder Folien-DMS.
Der Piezoeffekt
Piezoelektrische Kraftaufnehmer basieren auf mikroskopischen Deformationen in der atomaren Struktur eines speziellen kristallinen Materials. Quarz ist beispielsweise ein derartiges, natürlich vorkommendes piezoelektrisches Material. Durch Deformation seiner kristallinen Struktur ändern sich die elektrischen Eigenschaften derart, dass es zu Ladungsverschiebungen innerhalb des Materials kommt. Über eine entsprechende Elektronik kann diese Ladungsänderung in ein Spannungssignal umgewandelt werden, welches zur einwirkenden Kraft proportional ist (Seyfarth, 2012, S. 90).
Kraftplattformen
Die auf den menschlichen Körper am häufigsten wirkende Kraft ist die Bodenreaktionskraft. Diese kann durch einen dreidimensionalen Vektor beschrieben werden und besteht aus einer vertikalen Komponente und zwei Scherkomponenten entlang der Kraftplattenoberfläche (anterior/posterior - medial/lateral). Eine 4. Variable wird benötigt, um den Ursprung (Druckzentrum) des Bodenreaktionsvektors zu bestimmen (Winter, 2009, S. 117f.).
Kraftmessplatten sind Geräte zur Messung von Bodenreaktionskräften. Die häufigste Bauform einer Kraftplattform besteht aus einer Platte mit Kraftaufnehmern in den vier Ecken.
Mehrdimensionale Kraftmessung
Um Kräfte in zwei oder mehr Richtungen zu messen, werden zwei- oder dreiachsige Kraftaufnehmer benötigt. Diese bestehen einfach aus einer Kombination von einachsigen Kraftaufnehmern, welche rechtwinklig zueinander angeordnet sind. Das Hauptproblem ist hierbei sicher zu stellen, dass die einwirkende Kraft durch die Hauptachsen der jeweiligen Kraftsensoren verläuft (Seyfarth, 2012, S. 88).
<spoiler|Welche Information kann durch Kraftmessung gewonnen werden?>
• Kraftvektor F(t) und seine Komponenten unabhängig vom Ort des Angriffspunktes
• Vertikales Drehmoment
• Kraftangriffspunkt am Boden (Centre of Pressure)
• Horizontale Momente
</spoiler>
Kraftangriffspunkt
Der Kraftangriffspunkt (COP) ist definiert als der Schnittpunkt des resultierenden Kraftvektors mit der Plattenoberfläche (s. Abb. 3). Bei Platten mit Piezosensoren errechnen sich die Koordinaten des COP ($X_1, Y_1$) durch das Verhältnis der vertikalen Teilkräfte ($F_{00}$, $F_{X0}$, $F_{0Y}$, $F_{XY}$) zur vertikalen Gesamtkraft $F_z$ (Schwameder, 2009, S. 112ff.), wobei gilt
;#; $F_z = F_{00} + F_{X0} + F_{0Y} + F_{XY}$. ;#;
Wenn alle vier Kräfte gleich sind, befindet sich der COP genau in der Mitte der Kraftmessplatte, bei ($\frac{X}{2}$, $\frac{Y}{2}$). Im Allgemeinen gilt (Winter, 2009, S. 118),
;#;
$X1 = \frac{x}{2}\ (1 + \frac{(F_{X0} + F_{XY}) - (F_{00} + F_{0Y})}{F_z})$
;#;
;#; $Y1 = \frac{y}{2}\ (1 + \frac{(F_{0Y} + F_{XY}) - (F_{00} + F_{X0})}{F_z})$ ;#;
Auf eine genauere Herleitung dieser Formeln wird im Tutorial MMB2 näher eingegangen.
Anwendung: Instrumentiertes Laufband
Moderne Kraftmessplatten können in ihrer Dimension (Plattengröße) und Messgenauigkeit vielen biomechanischen Anforderungen sehr gut gerecht werden. Gerade beim Laufen möchte man allerdings eine Reihe von Schritten untersuchen. Hier helfen Kaskaden (Reihen) von Kraftplattformen, mit welchen einige Schritte hintereinander gemessen werden können. Die stationäre Messung von Laufbewegungen wird traditionell mit einem Laufband durchgeführt. Bislang war es nur sehr bedingt möglich gewesen, Kräfte unter dem Band ausreichend präzise zu messen. Inzwischen gibt allerdings Laufbänder, welche alle 3 Komponenten der Bodenreaktionskraft messen können (Seyfarth, 2012, S. 99ff.).
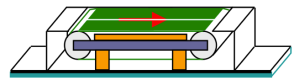
Das instrumentierte Laufband ADAL3D-WR ist für die Messung von Bodenreaktionskräften während des Gehens und Laufens entwickelt worden. Insgesamt besteht es aus 20 piezoelektrischen Sensoren zur genauen Bestimmung der 3D-Kraftvektoren und des Druckmittelpunktes (COP) für jede Seite.
Das Laufband verfügt über zwei Messplattenebenen. Auf der oberen Ebene befinden sich zwei Messplatten (s. Abb. 4, grüne Platten), um die vertikalen Kräfte zwischen dem linken und dem rechten Bein in der Doppelstandphase zu separieren. Die untere Ebene (Sensor S1-S4) misst die Horizontalkräfte.
Zusammenfassung
Fragen
- Worin könnte der Unterschied zwischen piezoelektrischen / piezoresistiven Kraftaufnehmern liegen?
- Nennen Sie mind. zwei Anwendungsgebiete für die Messung mit piezoelektrischen/-resistiven Sensoren.
- Welche Probleme könnten bei der Bestimmung des Kraftangriffspunktes (Centre of Pressure, COP) mit einer Kraftplattform entstehen?
Literatur
Baumann, W. (1985). Grundlagen der Biomechanik. Studienbrief zur Fort- und Weiterbildung von Trainern des Deutschen Sportbundes. Köln: Trainingsakademie Köln.
Schwameder, H. (2009). Dynamometrie. In A. Gollhofer (Hrsg.), Handbuch Sportbiomechanik (S. 88-103). Schorndorf: Hofmann.
Seyfarth, A. (2012). Kraftmessung. Präsentationsfolien im Rahmen des PS Messwertaufnahme und -verarbeitung SS 2012. Darmstadt: Institut für Sportwissenschaft.
Wick, D. (2009). Biomechanik im Sport. Lehrbuch der biomechanischen Grundlagen sportlicher Bewegungen. Balingen: Spitta Verlag GmbH & Co. KG.
Winter, D. A. (2009). Biomechanics and Motor Control of Human Movement. Hoboken, New Jersey: John Wiley & Sons, Inc.