Inhaltsverzeichnis
DYN1 Bewegungsgesetze
| Modul | DYN1 Newton'sche Axiome |
|---|---|
| Kategorie | Dynamik |
| Autor | Gossmann, Tokur |
| Voraussetzung | – |
| Bearbeitungsdauer | ca. 20 Minuten |
Lernziele
| Lehrveranstaltung | Lernziele |
|---|---|
| PS Biomechanik | - Funktion und Auswirkungen der Gesetzmäßigkeiten |
Einleitung
Isaac Newton hat 1687 die newton'schen Gesetze (auch Newton'sche Axiome genannt) als Grundgesetze der Bewegung formuliert. In diesem Modul werden diese Grundsätze vorgestellt:
- Trägheitsgesetz
- Grundgesetz der Dynamik
- Wechselwirkungsgesetz
- Superpositionsgesetz
Die Gesetze dienen als Grundlage, mit deren Hilfe Vorhersagen getroffen werden können, um die durch Kräfte hervorgerufene Bewegungen eines Körpers zu bestimmen.
Trägheitsgesetz
Die Trägheit ist „die Eigenschaft eines Körpers, seinen Bewegungszustand beizubehalten … [und] drückt sich im Beharrungsvermögen des Körpers aus, d.h., der Körper übt einen Widerstand gegenüber Änderungen seines Bewegungszustandes aus“ (Wick, 2009, S.46). Dieser Zusammenhang wird als Trägheitsgesetz (1. Newton'sches Gesetz) bezeichnet. Es besagt, dass ein Objekt so lange in seinem Zustand der Ruhe oder gleichförmigen Bewegung bleibt bis ein Kraft diesen Zustand ändert (vgl. Kassat, 1993, S. 9; Wick, 2009, S.46). Dies bedeutet, dass immer eine Kraft wirken muss, wenn ein Objekt seinen momentanen Zustand ändern soll.
Mathematisch kann das Trägheitsgesetz wie folgt ausgedrückt werden: (Seyfarth, 2004, S.8).
Ist die Geschwindigkeit konstant (gleichförmige Bewegung), ist die Summe aller Kräfte , die auf den Körper einwirken, gleich (in einem abgeschlossenen System).
Ableiten lässt sich das Trägheitsgesetz aus dem 2. Newton'schen Axiom: . Demnach „ruft eine Kraft eine Beschleunigung hervor, die schließlich den Bewegungszustand oder die Geschwindigkeit eines Körpers ändert“ (Wiemeyer & Passig, 2006, Glossar > Trägheitsgesetz).
Beispiel
Viele sportliche Bewegungen sind dadurch charakterisiert, dass sie aus einem Zustand der Ruhe in einen Bewegungszustand versetzen. Beispiele hierfür sind: Tiefstart bei Sprintdisziplinen, Startsprung beim Schwimmen, Übungsbeginn beim Turnen oder den Sportspielen. Aber auch bei Richtungsänderungen, z.B. eine Finte im Fußball oder das Abbremsen bzw. Beschleunigen während zyklischer Bewegungen sind Beispiele dafür, dass Kräften wirken müssen um Zustandsänderungen hervorzurufen (vgl. Wick, 2009, S.46).
Grundgesetz der Dynamik
Das 2. Newtonsches Axiom beschreibt den „Zusammenhang und die Abhängigkeit zwischen den mechanischen Größen Kraft [], Masse und Beschleunigung “ (Wick, 2009, S.47). Es besagt, dass „die Änderung des Bewegungszustandes … zur eiwirkenden Kraft proportional [ist] und längs der Wirkungslinie der Kraft [geschieht]“ (Wick, 2009, S.47).
Dieser Zusammenhang mit seiner fundamentalen Bedeutung für die gesamt Mechanik wird als Grundgesetz der Dynamik oder Dynamisches Grundgesetz definiert: . Die Einheit der Kraft ist Newton und setzt sich aus den Einheiten für Masse und Beschleunigung zusammen. Sie wird angegeben in .
„Die Masse kennzeichnet die Eigenschaft eines Körpers, sich der Bewegungsänderung zu widersetzen. Sie ist ein Maß für die Trägheit des Körpers und verkörpert somit den Proportionalitätsfaktor“ (Seyfarth, 2011, S. 5). Hieraus ergibt sich, dass sich Beschleunigung und Kraft proportional zueinander verhalten: .
Beispiel
Die Kraft mit der ein Boxer zuschlägt ist also abhängig von seiner Masse (der Einfachheit halber, wird die Faust isoliert betrachtet) und der Beschleunigung. Will er seine Schlagkraft erhöhen, hat er zwei Möglichkeiten:
- Erhöhen der Masse (was im Falle seiner Faust schwierig sein wird)
- Erhöhen der Beschleunigung (damit sich die Endgeschwindigkeit erhöht)
Wechselwirkungsgesetz
Das Wechselwirkungsgesetz (3. Newtonsches Axiom), auch unter dem Begriff bekannt, besagt dass die von zwei Körper aufeinander ausgeübten Kräfte (Wirkung und Gegenwirkung) gleich groß und in entgegengesetzter Richtung gerichtet sind (vgl. Seyfarth, 2003, S. 10). Dies bedeutet, dass der Betrag der Kraft, die ein Mensch auf ein Objekt (z.B. Medizinball) ausübt, auch auf ihn selbst einwirkt (vgl. Abb. 1), nämlich: .
Beispiel
Versucht ein Sportler einen schweren und schnell fliegenden Ball zu fangen, so kann es passieren, dass dieser Sportler nach hinten aus dem Gleichgewicht gerät. Während der Sportler mit seinem Körper eine Kraft auf den Ball ausübt, die die Geschwindigkeit des Balles abbremst, erhält der Körper eine Reaktionskraft , die ihn nach hinten beschleunigt. (vgl. Kassat, 1993, S. 27 f. zitiert nach Wiemeyer & Passig, 2006).
Weitere Beispiele, Aufgaben, Übungen sowie ein Quiz (dabei werden auch Themen aus zukünftigen Wissensmodulen berücksichtigt) finden sich hier.
Superpositionsgesetz
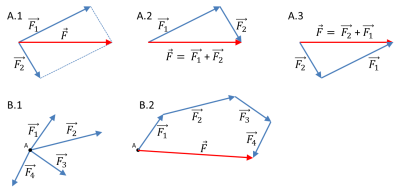
Das Superpositionsgesetz (4. Newton'sches Axiom) besagt, dass mehrere Kräfte, die auf einen Körper wirken, via Vektoraddition zu einer resultierenden Kraft aufsummiert werden können(vgl. Seyfarth, 2004, S. 12).
Die allgemeine Formel für eine Vektoraddition sieht folgendermaßen aus:
In Abb. 2 sind zwei Beispiele gegeben, hierbei sind die wirkenden Kräfte (blau) und die resultierende Kraft (rot) eingezeichnet. Abb. 2A zeigt eine einfache Vektoraddition zweier Vektoren. Zudem wird gezeigt, dass die Reihenfolge (vgl. A.2 bzw. A.3) keine Rolle spielt, denn das Ergebnis bleibt dasselbe. Abb. 2B zeigt eine komplexere Vektoraddition nach dem selben Schema: B.1 zeigt die wirkenden Kräfte, B.2 die Vektoraddition (blau) und die resultierende Kraft (rot).
Beispiel
Die Abwurfgeschwindigkeit beim (schrägen Wurf) ergibt sich aus der Horizontalgeschwindigkeit und der Vertikalgeschwindigkeit: . Die Erdanziehung wird in diesem Beispiel nicht berücksichtigt. Die Richtung in die die Kugel beschleunigt wird, ist durch die Addition der wirkenden Kräfte vorbestimmt.
Zusammenfassung
In diesem Podcast werden die 4 Gesetze der Newtonschen Mechanik nochmals aufgelistet und ausführlich erläutert.
Exkurs: Gravitation
Dieser Exkurs ist für die besonders Wissbegierigen unter euch. Hier lüften wir das Geheimnis der Gravitationskonstante und erklären wie Michell und Cavendish diese damals ermittelt haben. Schaut auf jeden Fall rein, es lohnt sich!
Kontrollfragen
<spoiler |1. Finde für jedes Newton'sche Axiom ein Beispiel aus dem Sport. Begründe deine Wahl!>
Für das Trägheitsgesetz ist beinahe jeder sportliche Start ein gutes Beispiel, denn die Trägheit des Körpers muss überwunden und in Bewegung versetzt werden. Auch um einen Körper abzubremsen und zum Stehen zu bringen, muss man die Trägheit überwinden. Beim Turnen zum Beispiel ist es wichtig, dass man auf der Stelle stehen bleibt, wenn man eine Übung beendet hat und nicht durch Restschwung kippt oder einen Ausgleichsschritt macht.
Das Grundgesetz der Dynamik ist im Sport sehr oft zu finden. Ein beliebiges Beispiel ist zum Beispiel das Runterdrücken von Pedalen beim Radfahren. Dazu wird Kraft benötigt. Hat man ein sehr massiges Bein, benötigt man nicht so viel Beschleunigung um dieselbe Kraft zu erzeugen wie mit einem sehr dünnen Bein.
Das Wechselwirkungsgesetz lässt sich zum Beispiel am Handstützüberschlag erläutern. Der Turner drückt sich während dieser Turnbewegung am Boden mit beiden Händen ab. Der Boden gibt dieselbe Kraft an den Turner zurück, sodass dieser wieder vom Boden weggestoßen wird.
</spoiler>
<spoiler |2. Wieso ist die Beschleunigung ein wichtiger Faktor im sportlichen Training? Begründe!> Im Sport muss der Körper ständig in einen anderen Bewegungszustand (beispielsweise vom Stehen ins Rennen oder auch andersherum) gebracht werden oder seine Bewegungsrichtung ändern. Dafür sind Beschleunigungen nötig, weswegen sie ein wichtiger Faktor im sportlichen Training sind. </spoiler>
<spoiler |3. Wodurch erfahren Objekte eine Zustandsänderung?> Ein Objekt ändert seinen Zustand, wenn von außen eine Kraft einwirkt. Das Objekt kann dadurch verformt werden oder seine Geschwindigkeit (durch Beschleunigung oder Abbremsen) ändern. </spoiler>
<spoiler |4. Warum kann ein Mensch in die Höhe springen? Erkläre dies anhand eines der Newton'schen Axiome!>
Warum ein Mensch in die Höhe springen kann, lässt sich gut mit dem Wechselwirkungsgesetz erklären.
Der Mensch drückt sich am Boden ab - es wirkt eine Kraft auf den Boden. Aufgrund des Wechselwirkungsgesetzes wirkt genau dieselbe Kraft auch auf den Menschen und er wird durch sie nach oben befördert, springt also in die Höhe.
</spoiler>
Literatur
Seyfarth, A. (2011). Grundlagen der Biomechanik. Teil B: Dynamik. Präsentationsfolien im Rahmen des PS Biomechanik WS 2011/12. Darmstadt: Institut für Sportwissenschaften.
Wick, D. (2009). Biomechanik im Sport - Lehrbuch der biomechanischen Grundlagen sportlicher Bewegungen (2. überarbeitete und erweiterte Auflage). Balingen: Spitta.
Wiemeyer, J. & Passig, D. (2006). BioPrinz - Biomechanische Prinzipien im Sport. Zugriff am 30.07.2013 unter: http://bioprinz.ifs-tud.de.