Inhaltsverzeichnis
WP1207 Springen
Modul-Infos
| Lehrveranstaltung | Lernziele |
|---|---|
| PS Forschungsmethoden 2 | - Verschiedene Sprungarten kennen- und differenzieren lernen - Grundlagen naturwissenschaftlicher Betrachtung von Sprüngen kennen - Biomechanische Aspekte von Sprüngen kennenlernen |
Einleitung
Das Springen gehört zu den elementarsten Bewegungen im Sport und Alltag.
Als Sportler muss man Hindernisse überspringen, Höhen erreichen oder Distanzen überspringen. Jeder Sprung hat dabei seinen individuellen Charakter was Ausführung und Ziel betrifft. Im Folgenden möchten wir die drei elementaren Sprünge „Squat-Jump“, „Drop-Jump“ und „Countermovement-Jump“ vorstellen und näher beleuchten.
Hier ein kurzer Überblick über das was kommt:
- kurze Wiederholung der wichtigsten Grundlagen
- kurzes Intermezzo zur Berechnung der Sprunghöhe
- Squat-Jump
- Countermovement-Jump
- Drop-Jump
Ausgewählte biomechanische Aspekte der Sportart
Wiederholung der Grundlagen
Bevor wir mit der eigentlichen Arbeit beginnen, wollen wir zunächst nochmal einen kleinen Überblick über die wichtigen Dinge des Lebens geben: Kräfte.
Bei jeder Form des Sprungs wirken verschiedene Kräfte auf den Körper. Die für uns interessanteste Kraft beim Springen ist aber die Gewichtskraft.
Wollen wir abspringen, so müssen wir dieser (Gewichts)Kraft entgegenwirken. Warum?
Die Gewichtskraft ist die Kraft, die dafür sorgt, dass wir Menschen auf der Erde bleiben und nicht “abheben”. Daher wird die Gewichtskraft auch als “Erdanziehungskraft” bezeichnet. Sie wirkt senkrecht zum Boden auf unseren Körper, drückt uns somit nach unten.
Mathematisch lässt sich die Gewichtskraft so ausdrücken: FG = m * g.
Besprechen wir kurz diese Formel:
m beschreibt die Masse, die ein Körper hat und wird in kg angegeben;
g beschreibt die Größe der Beschleunigung die dieser Körper erfährt und wird in m/s² abgegeben.
Das g wird üblicherweise als ‘a’ geschrieben. Da es sich hier aber um eine besondere Form der Beschleunigung handelt (nämlich der Erdbeschleunigung) wird hier die Beschleunigung als Konstante ‘g’ mit dem Wert von 9.81m/s geschrieben. Dieser Wert ist ortsabhängig.
Näheres dazu kann man hier nachlesen:
Sport-Wiki: aeussere_kraefte
Wikipedia: Gewichtskraft
Grundwissen: Gewichtskraft
Um das Prinzip der Kräfte zu verstehen müssen wir noch etwas einführen: das “dritte newtonsche Axiom”. Dieses beschreibt das “actio-reactio”-Gesetz. Vereinfach heißt das: Auf jede Kraft, wirkt eine entgegengesetzt wirkende Gegenkraft mit genau der gleichen Größe, sodass beide Kräfte addiert 0 ergeben.
Mathematisch bedeutet das: F1 + F2 = 0 oder F1 = -F2.
Beim Menschen bedeutet dies nun, dass der Gewichtskraft, eine mit der gleichen Kraft in die entgegengesetzte Richtung (also nach oben) entgegenwirken muss, um nicht auf den Boden gedrückt zu werden. Dieses Gesetz gilt es beim Sprung zu “überwinden”.
Ein weiterer Aspekt, den wir kurz anreißen möchten, sind die biomechanischen Grundprinzipien. Beim Sprung spielt vor allem das Prinzip des optimalen Beschleunigungsweges eine tragende Rolle.
Durch dieses Prinzip soll einem Körper, Sportgerät, etc. eine möglichst hohe Endgeschwindigkeit vermittelt werden. Dabei ist aber nicht der maximale Beschleunigungsweg von Bedeutung, sonder der optimale.
Dieses Prinzip lässt sich am Beispiel des Strecksprungs gut verdeutlichen: geht man tiefer in die Hocke, verlängert sich zwar der Beschleunigungsweg aber auf Grund der dadurch entstehenden schlechteren Hebelverhältnisse entsteht ein schlechteres Ergebnis.
Für mehr Informationen zu den biomechanischen Prinzipien klicke hier.
Ein Sprung lässt sich auch grafisch in einem Kraft-Zeit-Diagramm darstellen. Um dieses Diagramm zu erstellen, benötigt man ein technisches Hilfsmittel, welches wir im Folgenden noch kurz vorstellen möchten:
Die Kraftmessplatte
Die Kraftmessplatte ist ein Instrument, um vertikale Kräfte zu messen. Ihr Aufbau ist recht einfach; am Besten lässt sich dieser an einer Zeichnung erkennen:

Die Kraftmessplatte hat zwischen zwei Platten (Holz, Plastik, etc.) Drucksensoren, sogenannte piezoelektrische Sensoren. Diese reagieren auf Druck mit dem Aufbau eines elektrischen Feldes was wiederum zur Veränderung der elektrischen Spannung führt. Diese ist messbar und kann dann durch verschiedene Berechnungen als Kraft ausgedrückt werden.
Kurz gesagt:je höher der Druck auf die Sensoren, desto höher ist die Veränderung der Spannung und desto höher ist die Kraft.
Der Aufbau ist bei der Form der Messplatte nahezu gleich. Sie unterscheiden sich lediglich in ihrer technischen Raffinesse was die Größe von Bauteilen und Messpräzision angeht. Für wenig Geld kann man sich aber schon seine eigene Kraftmessplatte selbst zusammenbauen. Wer daran Interesse hat, findet hier eine Anleitung.
Wer sich immernoch nichts Wirkliches unter einer Kraftmessplatte vorstellen kann, schaut sich einfach mal das Wii Balance board an. Dieses Gerät ist nichts anderes, als eine Kraftmessplatte.
Hier nochmal ein Video, das die Funktionsweise der Kraftmessplatte darstellt.
Mit Hilfe der Kraftmessplatte können wir nun also die Kräfte bestimmen lassen, die bei einem Sprung wirken. Jetzt gilt es, diese sinnvoll zu verwerten und Werte zu berechnen, mit denen man tatsächlich etwas anfangen kann.
Da bei Sprüngen vor allem die Sprunghöhe interessant ist, wollen wir diese nun festhalten.
Wie das funktioniert, soll im folgenden Intermezzo erklärt werden.
---------------------------------------------------------------------------------------------------------------
Intermezzo zur Messung der Sprunghöhe
Nun stellt sich nur noch die Frage, wie wir die Flughöhe ermitteln können?!
Hierzu gibt es drei Möglichkeiten:
1) Zentimeterskala
Am einfachsten ist es über eine an der Wand angebrachte Zentimeterskala abzulesen wie hoch der Sprung war. Hierbei ist es am Besten den Sprung auf Video festzuhalten.
2) aus dem im Absprung erzeugten Kraftstoß
Der Kraftstoß ist identisch mit der Fläche unter der Kraft-Zeitkurve, d.h. je größer diese Fläche ist, desto höher ist die Abfluggeschwindigkeit v und damit auch die Flughöhe.
F * t = m * v (Verweis: Kraftstoß und Impuls)
(Kraftstoß) und (Impuls)
Mit der bekannten Masse des Springers kann die Abfluggeschwindigkeit berechnet werden und aus dieser wieder die Flughöhe.
3) aus der Flugzeit
Mit einer Videoaufnahme kann man ziemlich genau die Flugzeit bestimmen. Wer über eine solche Möglichkeit verfügt, sollte sie nutzen. Die Bestimmung der Flughöhe erfolgt dann über die folgende Formel:
h = 1/2 g * t22 (g = 9,81 m/s2 und t = Flugzeit in Sekunden)
Die verwendete Formel beschreibt den freien Fall eines Gegenstandes aus einer bestimmten Höhe. Lässt man z.B. einen Stein von einem Turm fallen, kann man durch Stoppen der Zeit bis zum Aufprall auf dem Boden die Höhe, aus der der Stein gefallen ist berechnen. Da wir beim Strecksprung aber eine aufsteigende Phase und eine absteigende (Fall-) Phase haben, halbieren wir die Flugzeit beim Sprung:
h = 1/2 g * (t/2)2
---------------------------------------------------------------------------------------------------------------
Diese Grundlagen sollten nun ausreichen, um zu verstehen, was bei den einzelnen Sprüngen passiert. Auf Formeln, die hin und wieder auftauchen können, wird zur Vertiefung gesondert verwiesen.
Viel Spaß! :)
Squat-Jump
Der Squat-Jump ist ein Sprung, der von der Hockposition heraus ausgeführt wird. Die Beine haben nun die Aufgabe in möglichst kurzer Zeit viel mehr Kraft als die Gewichtskraft aufzubringen und damit den Sportler zum Absprung zu bringen. Ziel ist es so hoch wie möglich zu springen, jedoch ohne aktive Bewegung der Arme (sie liegen an der Hüfte an). Somit gibt es keine Ausholbewegung und auch keine koordinativen Elemente. Um nun den Sprung besser verstehen zu können, wollen wir uns nun einmal die Kraft-Zeit-Kurve ansehen:
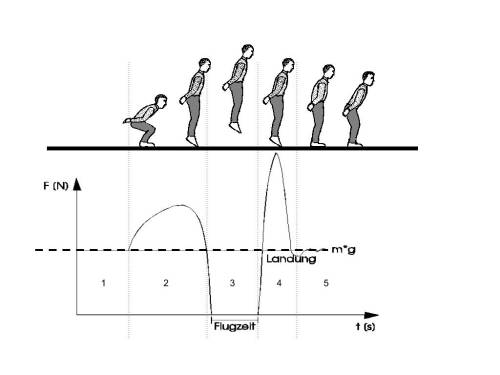
Hier ist zu erkennen, dass der Kraft-Zeitverlauf zunächst auf Gewichtskraftniveau beginnt, ehe er mit Beginn der Streckbewegung stark ansteigt. Wird der Boden verlassen fällt die Anzeige auf Null. Im Landemoment steigt die Kraft dann stark an und pendelt sich auf Gewichtskraftniveau wieder ein.
Das Aufstehen
In der ruhigen Hockstellung zu Beginn des zum Absprung führenden Streckens der Beine, haben diese noch die Funktion, die Stützkraft aufzubringen, die der Sportler zum ruhigen Stand benötigt. Factio = FG (Aktionskraft = Gewichtskraft)

Nun haben die Beine die Aufgabe, in möglichst kurzer Zeit viel mehr Kraft als die Gewichtskraft aufzubringen, um den Sportler möglichst schnell aufwärst zu bewegen und so zum Absprung zu bringen. So muss also Factio größer als FG werden, damit die resultierende Kraft Fres den Sportler aufwärts beschleuningt.

Im ersten Schritt wird die Reaktionskraft auf ihrer Wirkungslinie zum Körperschwerpunkt (KSP) verschoben und im Zweiten Schritt werden Freactio und FG zu Fres vektoriell addiert.
Hier noch zwei Abblidungen, um den Verlauf der vertikalen Bodenreaktionskraft beim Aufstehen zu veranschaulichen:
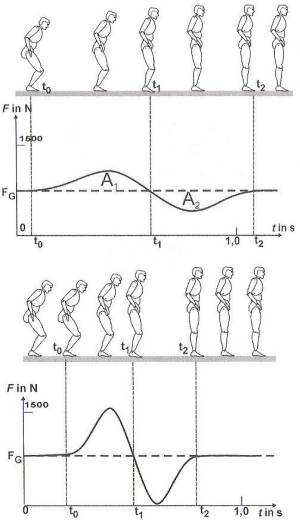
Auf der y-Achse ist die Kraft in Newton zu sehen und auf der x-Achse die Zeit in Sekunden.
Wir sehen oben eine langsame Ausführung und unten eine deutlich schnellere des Aufstehens. Bei t0 beginnt die Aufwärtsbewegung, bei t1 ist sie am schnellsten, bei t2 ist sie beendet. A1 ist der Kraft- bzw. Beschleunigungsstoß und A2 der Bremsstoß.
Für die Kraft-Zeitkurve ist typisch, dass sie mit einer Horizontalen Linie auf Höhe der Gewichtskraft FG beginnt und je schneller der Sportler sich aufrichtet, desto höher werden der Wellenberg und das Wellental..
Der Absprung
Um den Absprung zu veranschaulichen, hilft uns wieder folgende Abbildung:

Es ist ein typischer Squat-Jump zu sehen. Bis t0 ist der Sportler in ruhiger Hockstellung. Von t0 bis t1 beschleunigt er nach oben und nach t1 fällt die Streckkraft unter die Gewichtskraft FG, d.h. der Sportler kann nicht mehr nach oben weiter beschleunigen und verlässt bei t2 den Boden. Die Fläche A beschreibt ein Maß für die erreichte Maximalgeschwindigkeit beim Hochgehen, ist t1 nahezu gleich t2, ist diese fast identisch mit der Abfluggeschwindigkeit.
Der ideale Squat-Jump
Zum Abschluss noch drei verschiedene Ausführungen des Squat-Jumps:
1) zu tiefe Hockstellung
2) sehr gut gelungener Squat-Jump
3) zu aufrechte Stellung

1) Hier ist die Ausgangssituation, dass der Sportler in einer zu tiefen Hockstellung begonnen hat. Aus ihr heraus ist es kaum möglich, große Kraftwerte zu entwickeln. Obwohl eine längere Beschleunigungszeit bzw. ein längerer Beschleunigungsweg genutzt wird, ist der Wert von A nicht besonders groß.
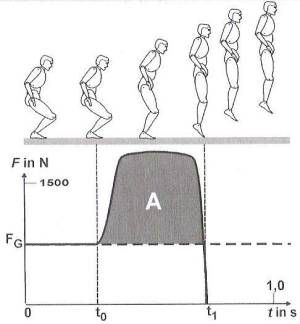
2) Hier erreicht der Sportler eine beinahe ideale Absprungkurve, weil er sehr schnell auf eine große dynamische Maximalkraft kommt und diese auf fast bis zum Verlassen des Bodens halten kann. Es lässt sich also ableiten, dass der (theoretisch) ideale Kraft-Zeit-Verlauf eines Squat-Jumps ein rechteckiger Verlauf ist.

3) Nun haben wir die Ausgangssituation, dass der Sportlerin einer zu aufrechten Stellung begonnen hat. Aus ihr herraus ist es kaum möglich lange genug zu beschleunigen.
Fazit
Es gibt für jeden Sportler nur einen optimal langen Beschleunigungsweg und nicht den maximal langen Weg aus der tiefsten Hockstellung heraus. Man muss durch viele Sprungversuche herausfinden, wie dieser optimal lange Weg ist.
Countermovement-Jump
Der Countermovement-Jump wird eingesetzt um die Kraftfähigkeit der Sprungmuskulatur zu testen (Explosionskraft).
Die Messung erfolgt durch einen Sprung aus dem Stand mit einer Ausholbewegung, die Hände sind dabei in die Hüfte gestemmt. Die Bewegung startet mit dem Tiefgehen durch Beugen der Sprung-, Knie- und Hüftgelenke. Das Tiefgehen wird abgebremst und in eine flüssige Hochgehbewegung umgeleitet, in der die Sprung-, Knie- und Hüftgelenke durchgestreckt werden. Die Streckung der Gelenke erfolgt dabei so explosiv, dass der Sportler am Ende der Streckung vom Boden abhebt und eine Flugphase eingeleitet wird. Dieser Sprung wird meist auf einer Kraftmessplatte durchgeführt.
Um den Countermovement-Jump besser verstehen zu können, wollen wir uns nun einmal den Kraft-Zeit-Verlauf ansehen:

Hier ist zu erkennen, dass der Sportler zunächst in einem ruhigen Stand auf der Plattform steht. Die Kraft befindet sich auf Gewichtskraftniveau. In Phase 1 sehen wir, dass mit Beginn der Ausholbewegung die Stützkraft abfällt, hier nimmt auch die Geschwindigkeit zu. Phase 2 wird mit dem Umkehrpunkt eingeleitet, hier reduziert sich die Geschwindigkeitszunahme, sobald die Kurve wieder die Gewichtskraft erreicht hat, folgt die Abbremsung der Abwärtsbewegung(Phase3). Hier wird der tiefste Punkt der Ausholbewegung erreicht. Die Kraftwerte liegen nun deutlich über Gewichtskraftniveau. Durch die Streckung der Sprung-, Knie- und Hüftgelenke in Phase 4 wird ein weiterer Anstieg der Kraft erzeugt, dieser endet mit dem Abflug von der Platte, nun wirkt nur noch die Gewichtskraft auf den Körper.
Prinzip der Anfangskraft
Das biomechanische Prinzip der Anfangskraft spielt vor allem bei Wurf und Sprungbewegungen eine große Rolle. Hier soll eine hohe Endgeschwindigkeit des Körpers oder eines Sportgerätes erreicht werden. Das Prinzip sagt aus, dass durch eine einleitende Bewegung, entgegengesetzt der Hauptbewegungsrichtung, ein Leistungsvorteil bewirkt wird. Durch das Abbremsen der Gegenbewegung entsteht eine Anfangskraft, durch die der Kraftstoß(Impuls) vergrößert wird.
Um das Prinzip der Anfangskraft auf den Countermovement-Jump zu beziehen, schauen wir uns nochmal den obigen Kraft-Zeit-Verlauf an.
Durch die Ausholbewegung entgegen der Hauptbewegungsrichtung(Phase1) und die so erzeugte Vorspannung in der Sprungmuskulatur wird im unteren Umkehrpunkt(Phase 2) der Bewegung bereits eine positive Kraft erzeugt. Diese Kraft ist größer als die Kraft, die durch das eigene Körpergewicht erzeugt wird.
Tiefgehen

Bevor der Countermovement-Jump ausgeführt wird, steht der Athlet in einem aufrechten Stand. Der Sportler muss nun eine Stützkraft auf bringen, diese Stützkraft muss genau so groß sein wie seine Gewichtskraft, denn dann ist die resultierende Kraft null.
Vermindert der Sportler nun die Stützkraft, so beginnt das Tiefgehen, da die resultierende Kraft eine Kraft ist, die nach unten zeigt.
In der obigen Abbildung ist dies ab Zeitpunkt t0 der Fall.
Das Tiefergehen wird so lange schneller, wie der Sportler seine Stützkraft so reduziert, dass sie kleiner als die Gewichtskraft ist. In diesem Fall bis t1.
Bringt der Athlet nun Kraft auf, die größer als die Gewichtskraft (FG) ist, wird das Tiefergehen abgebremst, denn die resultierende Kraft richtet sich nun nach oben.
Das Abbremsen von t1 bis t2 ist beendet, wenn der Bremsstoß A2 so groß ist wie der von t0 bis t1 dauernde (abwärts gerichtete) Beschleunigungsstoß A1.
Hochgehen
Nach dem der Athlet den tiefsten Punkt der Ausholbewegung erreicht hat, folgt das Hochgehen, in Form eines Beschleunigungsstoßes.
Der Sportler streckt seine Beine und seinen Oberkörper durch. Zu Beginn des Beschleunigungsstoßes ist schon eine positive Anfangskraft vorhanden, welche größer ist als die Gewichtskraft des Sportlers (Siehe Prinzip der Anfangskraft).
Diese Anfangskraft ist auch die Ursache, dass eine größere Sprunghöhe erreicht wird. Durch das Durchstrecken der Sprung-, Knie- und Hüftgelenke, so wie des Oberkörpers entsteht eine so große Kraft, dass es den Sportler vom Boden abdrückt und die Flugphase eingeleitet wird.
Perfekter Countermovement-Jump
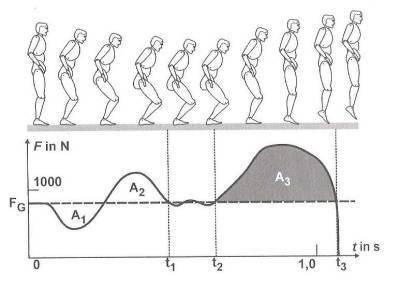
Eine gute Vorstellung von einer optimalen Kraft-Zeit-Kurve erhält man, wenn man sich zuerst eine nicht optimale Kraft-Zeit-Kurve ansieht. In der obigen Abbildung sieht man eine nicht optimale Kraft-Zeit-Kurve.
Das erste Wellental und der erste Wellenberg zeigt das Tiefgehen des Sportlers. Jedoch hat der Sportler hier in der Hocke eine kurze Pause eingelegt, was zur Folge hat, dass die Kurve wieder auf dem Niveau der Gewichtskraft verläuft.
Dadurch führt der Athlet einen Squat-Jump aus, da das Prinzip der Anfangskraft nicht umgesetzt wurde.
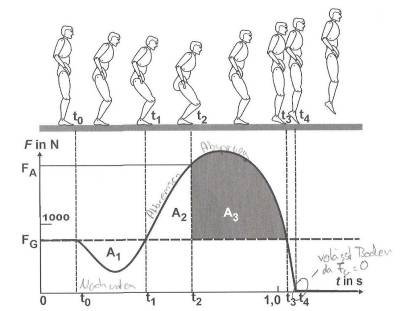
Für die optimale Ausführung eines Countermovement-Jumps, soll der Sportler zwar eine große Anfangskraft entwickeln, er soll jedoch nicht schon beim Abbremsen sondern erst in der Absprungphase sein Kraftmaximum einsetzen. Das Verhältnis des Bremsstoßes zum Beschleunigungsstoßes, also von A2 zu A3, soll etwa 1:2 sein.
Fazit
Die Größe der Anfangskraft ist für jeden Sportler optimal zu gestalten, nicht maximal. Ob die Gegenbewegung, das Beugen, sehr weit oder weniger weit ausgeführt wird, ist von der Leistungsfähigkeit des Sportlers abhängig.
Drop-Jump
Der Drop-Jump dient der Ermittlung der reaktiven Sprungkraftfähigkeit. Hierbei wird, im Gegensatz zu den beiden vorherigen Sprüngen, nicht vom Boden sondern von einer Erhöhung eingesprungen.
Die Arme des Sportlers sind an der Hüfte angelegt und verhindern somit eine zusätzliche Impulsübertragung.
Nach dem erzwungenen Tiefgehen werden die Sprung-, Knie- und Hüftgelenke gestreckt und der Absprung wird eingeleitet.Die Streckung kommt hauptsächlich aus dem Sprunggelenk und weniger aus dem Hüft- und dem Kniegelenk, wie bei den Sprüngen zuvor.
Das Ziel ist es ebenfalls die größtmögliche Flughöhe zu erreichen.
Kraft-Zeit-Kurve
Im Folgenden wollen wir den Sprung anhand einer Kraft-Zeit Kurve und der zugehörigen Bildreihe veranschaulichen:

Die Kraft-Zeit-Kurve beginnt auf der Nulllinie, da zum Zeitpunkt des Einspringens noch kein Kontakt zum Boden bzw. zur Kraftmessplatte besteht und somit noch keine Kraft auf Diese wirkt.
Ab dem Zeitpunkt t0 hat der Sportler den ersten Bodenkontakt.
Der Zeitpunkt t1 leitet das Abfangen der Energie in den Absprung ein. Durch den erhöhten Einsprung wirken bei der Landung größere Kräfte als bei einem Sprung aus dem Stand.
Dies lässt sich mathematisch beweisen: vereinfachen wir es, indem wir uns das Kräfteproblem am freien Fall anschauen; zunächst brauchen wir die Fallgeschwindigkeit. Diese erhalten wir über die Formel v = √(2*g*h).
Dabei ist h die Höhe, aus der Abgesprungen wird und g die Erdbeschleunigung (9,81m/s²).
Haben wir die Aufprallgeschwindigkeit, wollen wir ausrechnen, wie groß die Bremsbeschleunigung ist, d.h. wie „stark“ muss ich abbremsen/wieviel Kraft der Sportler in den Bremskraftstoß investieren muss. Dabei spielt es eine Rolle, wie tief man dabei in die Knie geht. Nehmen wir an, wir gehen 1m in die Knie. Die Bremsbeschleunigung erhalten wir nun über die Formel: aBrems = v2 /2s.
Dabei ist v die vorher berechnete Aufprallgeschwindigkeit und s die Strecke, die wir in die Knie gehen.
Zuletzt benötigen wir die Mutter aller Formeln um die Kraft zu berechnen, die bei der Landung wirkt: F = m * a.
Dabei ist m die Masse des Drop-Springers und a die zuvor Berechnete Bremsbeschleunigung. So sieht die Kraftformel aus, wenn man alle Werte direkt einsetzen möchte:
F = m * (2*g*h)/2*s.
Ab dem Zeitpunkt ab dem der Sportler seine eigene Gewichtskraft auf den Boden ausübt, muss er der entstehenden Bodenreaktionskraft (hervorgerufen durch den erhöhten Einsprung) entgegenwirken. Dies erreicht er durch das Beugen und rechtzeitige Strecken der Beine. Diese Bremsbeschleunigung (A2) dauert von t1 – t2 an. Ab t2 wirkt der eigentliche Absprungstoß (A3) bei welchem der Sportler mehr als seine Gewichtskraft auf den Boden aufbringt, um somit, als Folge des hohen Kraftstoßes, beim Zeitpunkt t4 den Boden zu verlassen.
Aus biomechanischer Sicht lässt sich dieses Phänomen anhand des dritten newtonschen Axioms erklären:
Bis zum Zeitpunkt t2 gilt: Factio > Freactio
Und ab dem Zeitpunkt t2 gilt: Freactio > Factio.
Das erzwungene Tiefgehen führt sofort beim ersten Bodenkontakt zu einer Vorspannung in der Sprungmuskulatur. Dadurch können Sportler mit einer hohen reaktiven Kraft eine höhere Anfangskraft entwickeln als durch das bloße Tiefgehen beim Countermovement-Jump.
Ein (nicht) optimaler Drop-Jump
Im Folgenden werden wir uns eine Kraft-Zeit Kurve eines nicht-optimalen Drop- Jumps ansehen:

Hier können wir deutlich erkennen, dass mehr Kraft für die Bremsbeschleunigung (A2) aufgebracht wurde als für den Beschleunigungskraftstoß (A3).
Aber woran liegt das?
Die Antwort liegt in der Einsprunghöhe des Sportlers.
Aufgrund derer wirkt eine größere Kraft auf den Sportler, der er entgegenwirken muss. Es fällt dem Sportler hier schwerer noch genügend Kraft für den Beschleunigungskraftstoß aufzubringen.
Dies ist sehr gut anhand der Kurve zwischen t1 und t2 zu sehen. Dadurch, dass das Kraftmaximum bereits vor dem eigentlichen Absprung einsetzt ist das Prinzip der Anfangskraft nicht richtig umgesetzt worden.

Hier sehen wir im Vergleich dazu einen optimalen Drop-Jump mit einem nahtlosen Übergang von Bremsbeschleunigung (A2) in den Beschleunigungskraftstoß (A3).
Hier ist zu erkennen, dass das Kraftmaximum erst während des Beschleunigungskraftstoßes stattfindet. Dadurch ist das Prinzip der Anfangskraft optimal genutzt worden.
Drop-Jump als Mittel zur Bestimmung der reaktiven Kraft
Wenn man den Drop-Jump für die Ermittlung der reaktiven Kraftfähigkeit einsetzt wird meist aus einer vorgegebenen Ausgangshöhe eingesprungen, um so den Bewegungsimpuls des Sportlers auf der Messplatte bestimmen zu können.
Je höher man also die Ausgangshöhe bestimmt, desto höher ist die Kraft, die auf den Sportler wirkt und dementsprechend muss mehr Kraft entgegenwirkt werden , damit eine optimale Sprunghöhe erreicht werden kann.
Einige Messparameter zur Bestimmung der reaktiven Kraftfähigkeit sind:
- Kontaktdauer auf den Boden
- Flughöhe ( oder Flugdauer)
- Reaktivitätsquotient (Flughöhe (oder Flugdauer) / Kontaktdauer)
Fragen zur Wiederholung
Zum Schluss möchten wir euch eine kleine Verständnisaufgabe zu den drei vorgestellten Sprüngen aus dem Buch „Angewandte Bewegungslehre und Biomechanik des Sport“ von Ullrich Göhner geben:
Auf dem Bild ist eine Bildreihe verschiedener Sprünge und Landungen zu erkennen.
Könnt ihr die verschiedenen Sprungformen erkennen und benennen?

Und für die Interessierten unter euch: Wie würde die Kraft-Zeit-Kurve zu dieser Bildreihe aussehen?
Wir wünschen euch viel Spaß bei der Bearbeitung 
Literatur
- Bilder: Squat-Jump
- Ulrich Göhner, Angewandte Bewegungslehre und Biomechanik des Sports, Tübingen 2008 (S.86, Abb. 5-4)
- Ulrich Göhner, Angewandte Bewegungslehre und Biomechanik des Sports, Tübingen 2008 (S.86, Abb. 5-5)
- Ulrich Göhner, Angewandte Bewegungslehre und Biomechanik des Sports, Tübingen 2008 (S.87, Abb. 5-6)
- Ulrich Göhner, Angewandte Bewegungslehre und Biomechanik des Sports, Tübingen 2008 (S.88, Abb. 5-7)
- Ulrich Göhner, Angewandte Bewegungslehre und Biomechanik des Sports, Tübingen 2008 (S.88, Abb. 5-8)
- Ulrich Göhner, Angewandte Bewegungslehre und Biomechanik des Sports, Tübingen 2008 (S.89, Abb. 5-9)
- Bilder: Drop-Jump
- Ulrich Göhner, Angewandte Bewegungslehre und Biomechanik des Sports, Tübingen 2008 (S.89, Abb. 5-21)
- Ulrich Göhner, Angewandte Bewegungslehre und Biomechanik des Sports, Tübingen 2008 (S.89, Abb. 5-23)
- Ulrich Göhner, Angewandte Bewegungslehre und Biomechanik des Sports, Tübingen 2008 (S.89, Abb. 5-24)
- Bilder: Countermovement-Jump
- Ulrich Göhner, Angewandte Bewegungslehre und Biomechanik des Sports, Tübingen 2008 (S.90, Abb. 5-12)
- Ulrich Göhner, Angewandte Bewegungslehre und Biomechanik des Sports, Tübingen 2008 (S.93, Abb. 5-20)
- Ulrich Göhner, Angewandte Bewegungslehre und Biomechanik des Sports, Tübingen 2008 (S.90, Abb. 5-11)
- Ulrich Göhner, Angewandte Bewegungslehre und Biomechanik des Sports, Tübingen 2008
Autoren
- Squat-Jump, Messung der Sprunghöhen: Tobias Storck
- Countermovement-Jump: Christoph Weber
- Drop-Jump, Zusammenfassung: Christian Schmitt
- Einleitung, Wiederholung der Grundlagen & Videos: Christoph Döringer
Bewertung des Wiki-Moduls
| Kategorie | Döringer | Schmitt | Storck | Weber | Anmerkungen |
|---|---|---|---|---|---|
| Inhalt (max. 10) | 6 Pkt | 6 Pkt | 6 Pkt | 8 Pkt | |
| Form (max. 5) | 3 Pkt | 3 Pkt | 3 Pkt | 4 Pkt | Übersichtlichkeit verbesserungsfähig |
| Bonus (max. 2) | 1 Pkt | 1 Pkt | 1 Pkt | 1 Pkt | Bezüge hergestellt, Bestimmung Reaktivkraft durch Dropjump, Intermezzo Sprunghöhen, Prinzip der Anfangskraft beim Hockstrecksprung |
| Einzelbewertung | 10 Pkt | 10 Pkt | 10 Pkt | 13 Pkt | 15 Punkte = 100% |
| Gesamtbewertung | 43/60 Punkte = 72% |
