Inhaltsverzeichnis
2018 Akhil S Anand
| Title | Generating Kinematics and Dynamics of Human-Like Walking Behaviour with Deep Reinforcement Learning |
|---|---|
| supervisor | Prof. Dr.-Ing. Hubert Roth, Prof. Dr. Andrè Seyfarth and M.Sc. Guoping Zhao |
| Author | Akhil S Anand (akhilsanand33@gmail.com) |
| Degree | Masters Mechatronics, University of Siegen. |
| Submission date | 14.11.2018 |
| Präsentationstermin | 14.11.2018 |
| Status | completed |
| Zuletzt geändert | 30.06.2019 |
<note important> Achtung: Benutzt diese Vorlage für eure Wiki-Einträge!! !! </note>
<note tip>
Hier findet ihr Hilfestellungen beim Formatieren des Wikis: HowTo - Wiki-Format
Hier gibt es Hilfe zum Erstellen eines Tutorials/Podcasts HowTo - Tutorial
</note>
Abstract
A dynamic model capable of reproducing rich human-like walking behaviours at both kinematic and dynamic levels could be a highly useful framework for developing state of the art control schemes for human assistive devices like exoskeletons, prosthesis and also for bipedal robots. Developing such a model is difficult, as it needs to capture all the complexities of human locomotion system since we don’t have a perfect understanding of the various interconnections within it. Here we demonstrate deep reinforcement learning based strategy to fill the gap of this illiteracy, as our model learned these interconnections mapping its input state space to the output action space in trial and error based method. The developed model (a 7 segment 14 DOF human lower limb muscle model actuated with 22 hill type actuators) is capable of generating robust human walking behaviour in a walking speed range of 0.6ms−1 to 1.2ms−1 at a specified target walking velocity withstanding hip perturbations. The reinforcement learning agent used the motion capture data of a human subject to learn the kinematic behaviour and a reference human muscle pattern to learn the muscle dynamics. Here we also implemented an optimization strategy for minimizing metabolic cost incurred during the walking gait. We further explored the possibilities of using a torque based control and muscle based control schemes for the model and found that the muscle based model is superior in generating robust walking behaviour. As developing robust human assistive control schemes being the main motivation for this work, we have tested a reinforcement learning based control strategy for a simple virtual hip-exoskeleton and found considerable amount of reduction in the metabolic cost. The results of this work underlines a huge possibility of developing robust human like locomotion behaviour at kinematic and dynamic levels using deep reinforcement learning techniques and using it to develop highly efficient control schemes for human assistive devices.
Motiovation and Introduction
Especially in the field of robotics, the researchers are trying adopt the creations of nature by trying to mimic them or trying to understand the underlying mechanisms behind them. It is a hard fact that with all this scientific knowledge the humanity has we are still far from understanding the underlying mechanism behind many natural creations, the human system being the perfect example. If not understanding we are also far from building efficient systems like the them, bipedal locomotion being the ideal example. Still we are living in an era of technological marvels where the humanity is behind building robots to superhuman suits. It is a high time where the demand for highly sophisticated human assistive technologies are on a high across various fields like rehabilitation, army, sports etc., making this research very relevant to the current time. This thesis is an effort to develop a model capable of reproducing human-like 3D walking behaviour at the kinematic and dynamics levels. The work from H.Geyer and S.Song [63] demonstrated dynamic 3D walking of a lower limb human model actuated using 22 hill type muscle actuators using a reflex based control. This model could produce inspiring results both at kinematic and dynamic levels and could execute various locomotion behaviours, such as: walking, running, stair/slope negotiation, turning and deliberate obstacle avoidance. We have adopted the lower limb musculoskeletal model from the above work for this thesis. It is also this is the time of unprecedented advancement in the area of reinforcement making use of deep neural networks, and this combination is surely very ideal to deal with our problem which is highly complex in nature. The reinforcement learning is slowly conquering the continuous domain problems ever since the advent of policy gradient based methods and we are witnessing significant progress every year in the area. Also recent works from Peng et al named deep-mimic and deep-loco [48, 53] are inspiring examples demonstrating capability of the state of the art deep reinforcement learning algorithms in modelling the human locomotion behaviour. One the other-way around, being a reinforcement learning enthusiast it also a huge motivation to challenge the reinforcement learning algorithms with such a complex task of modelling the human locomotion system. Having a robust model capable of reproducing human locomotion behaviours could have wide spread impact on various field such as human assistive technologies, robotics and also in the biomechanics research. This work is a first step toward a greater goal of developing a general human model which can reproduce a wide range of general human locomotion behaviours with main motivation of using this model to develop human assistive systems and robotic systems.
The human assistive systems like exoskeletons and prosthesis are the systems which needs to
work in tandem with human locomotion system to function efficiently. Decades of research
shows the difficult in approximating control schemes for such system because of the highly
complex and non-linear behaviour of the human system. Recently the human-in-loop optimization
techniques are gaining popularity in finding the optimal control schemes for such
devices [82, 19]. It is proved to be efficient way to tune the control schemes for exoskeletons
and prosthesis to be best suited for the individual requirements on the basis of minimizing the
metabolic cost. As the reinforcement learning theoretically has the capability to efficiently
approximate very complex control schemes, it should be an ideal fit for human assistive
controllers as they demand a complex control scheme to be efficient across the users. Also
reinforcement learning based controller surely need the human in loop optimization methods
for learning the control policy itself. In a crude way it could also be assumed as a huge
state-space controller with huge number of parameters to tune. But this needs relatively huge
number of samples to find the optimal policy, yes reinforcement learning is extremely sample
hungry. That correlates with need for modelling dynamic human behaviour in a computer
system so that the control policy learned on such as model could be transferred to individual
human controllers efficiently with minimum optimization effort on the final hardware.
Human Anatomy
Planes describing human anatomy
- Coronal Plane or Frontal Plane: The vertical plane dissecting the body sideways, this divides the body or any of the body parts into anterior and posterior sections.
- Sagittal Plane or Lateral Plane: The vertical plane running from the front to back, this divides the body or any of its parts into right and left sides.
- Axial Plane or Transverse Plane: The horizontal plane, divides the body or any of the body parts into upper and lower sections.
Skeletal structure
The human skeleton has a total of 206 bones, the entire skeletal system performs various functions to provide shape, support and protection to the human body. It also helps in providing attachments for muscles, to produce movement and to produce red blood cells in the body. The main bones of the human skeleton in the lower limb area are as follows:
- Pelvic girdle - Ilium, Pubis, and Ischium.
- Leg - Femur, Tibia, and Fibula.
- Ankle - Talus and calcaneus.
- Foot - Tarsals, Metatarsals, and Phalanges.
Skeletal joints
A joints are the connection made between the bones in the body which links the skeletal system to performs various movements. Human body contains many of these orthopaedic joints providing higher flexibility during movements. The main joints of the body are located at the hip, shoulders, elbows, knees, wrists, ankles fingers.
Joint Motions
The human body is well capable of making a tremendous range of movements with the help
of its synovial joints. All these joint movements are actuated by the contraction or relaxation
of the muscles that are attached to the bones on either side of the joints. Movement types are generally paired, with one directly opposite to the other. (see Fig. 4)
Muscle Structure
There are around 600 muscles in the human body and it accounts for nearly half of the human body weight. Human muscles are made up of specialized cells called muscle fibers and are attached to bones or internal organs or blood vessels. The contraction of these muscles are responsible for generating most of the movements in the body. Human locomotion is a result of an integrated action between joints, bones and skeletal muscles. Skeletal muscles are responsible for posture, joint stability, facial expressions, eye movement, respiration, heat production etc. (See Fig. 5)
Human Gait Cycle
Gait cycle of human walking is a complete cycle of walking starting from touch down of a leg to the touch down of the same leg which is basically two steps of walking. This includes stance and swing phase of both the left and right legs. A single gait cycle can be divided into two sections based on stance and swing condition of a leg as stance and swing phase respectively and can be further divided into single support phase and the double support phase. During a gait cycle of normal walking the stance phase takes around 62% of the gait cycle and the swing phase constitutes the remaining 38% of the gait cycle as shown in the figure 6.
Human Gait Modelling
The human gait modelling research has a history of approximately three centuries, but in the
old days researches were limited due to lack of measurement technologies. During then most of the researches were based on knowledge of human anatomy and observations of the human’s
daily locomotion behaviour. Currently with the abundance of advanced measurement
technology the gait modelling research has advanced heavily. There are different types of
gait models which are based on clinical analysis, structural models, musculoskeletal models
and neuro-muscular models.
- Clinical Gait Analysis: The clinical gait analysis are conducted to identify certain normal or pathological movements generally using simplified human model of the human body structure.
- Structural Models: In this approach human locomotion system is modelled only considering the structural relationship, which includes body mass, segment lengths and angles. In this method there are two different approaches. The first approach is considering the COG a linear path while in the second approach assumes that of an inverted pendulum. In this the second approach is very prominent where it proposes a biped model by simplifying the human body structure, by using the mechanical analogy of a simple pendulum as shown in figure 7.
- Musculoskeletal Models: There are different types of musculoskeletal models, out of them the EMG based models are very relevant. In this type of models surface electromyrography(EMG) is used to capture the muscle activation patterns. Then based on this EMG data along with the joint models relationships are developed to approximate the human locomotion. These models can then simulate the muscle activation patterns and identify the major muscle groups which are active during a particular motion Based on this result the joint moments and muscle strength can be approximated well.
- Neuro-muscular Models: Researchers has found out that the immense flexibility and stability of the human gait is achieved by the interaction between the nervous system and the musculoskeletal system Here the neuro-motor commands from the nervous system act as a high level controller for the locomotion system. The most important assumptions for the entire of neuro-muscular model development is the concept of a central pattern generator (CPG, which is responsible for the controlling the muscle-articular movements. CPG is located at a lower level of the central nervous system at the spinal cord, a hierarchical location of CPG.
EXOSKELETONS
In general, exoskeletons are defined as wearable robotic mechanisms for providing better mobility assistance to humans. General Electric developed the first professional exoskeleton device in the 1960s called HARDIMAN (Human Augmentation Research and Development Investigation). From then on the extensive research in the field of human assisting technologies helped the evolution of impressive and commercially available exo-suits. But still the area of control strategies for human assistance are still not highly flexible and robust.
This thesis will be considering lower extremity soft exo-suits as it is more relevant to this research. The human locomotion task is observed to be highly complex as it involves the coordination of brain nerves and muscles. And it’s always true that no two individuals possess identical locomotion styles. There are many important factors which could potentially affect the control strategies such as the walking style, aging, various diseases. But with development of fast computers and compact actuator and power technologies we are progressing faster to solve these challenges in the near future. But still the further development in actuator and power technologies will be able to accelerate the development in the field. Any general assistive exo suits could be classified into two types depending on the kind of structure building up the exoskeleton which are, soft and hard exoskeletons. Soft exoskeleton has very soft and flexible fixtures using belts which is a relatively new approach for exosuits, cables etc while the hard exoskeletons will have rigid links attached to the body. An example of soft exo-suit developed by harvard biodesign lab is shown in figure 8.
Human-in-the-loop Optimization
The exoskeletons work in parallel with human body and can be activated actively or passively. The control systems of the exoskeleton robots are entirely different from the traditional robots as the operator is always in the loop with system. Formally the human-in-the-loop based optimization method is described as a methods for automatically discovering, customizing, and continuously adapting assistance by systematically varying the device control in order to maximize the human performance [82]. Figure 9 shows the control scheme devised by J.Zhang et al based on human-in-the-loop optimization.
DEEP REINFORCEMENT LEARNING
Reinforcement learning
Reinforcement learning(RL) is an important type of Machine Learning approach where an agent learns how to properly behave in a given environment by performing actions and understanding the corresponding results. Reinforcement learning is learning is about mapping the states to actions so as to maximize a numerical reward signal. The learning agent here is not told directly about which actions to take, but instead the agent must discover which actions yield the most reward by trying all of them. In the most interesting and challenging problems, actions may affect not just the immediate reward but also the next state and, through that, all the subsequent rewards [67]. The basic idea of reinforcement learning is illustrated in figure 10. Where and agent is interacting with an environment by taking and actions and sensing and obtains some rewards as a result of these interactions. In the process agent is trying to perform the actions for maximizing the reward with a final goal of learning an optimal strategy for the task defined based on the reward function. With the optimal strategy, the agent is capable to actively adapting to the environment to maximize future rewards.
Reinforcement learning is different from both supervised and unsupervised methods, which are two most widely researched machine learning techniques at present. With clear distinction Reinforcement learning is third machine learning paradigm. The main challenge in RL which is not a criterion in any other machine learning methods is the trade-off between exploration and exploitation. Easy way to obtain higher reward for the agent is to perform the actions that it has tried in the past and found to be effective inproducing reward which is referred as exploitation. But at the same time it is import to discover such high paying actions it is important to try the actions that it has not selected before which is referred as exploration. The agent has two option it can either exploit what it has already experienced in order to obtain reward, but at the same time it needs to explore in order to make better action selections in the future. The agent always needs to go through the dilemma of exploration vs exploitation and this has to be managed optimally to get better results. The exploration-exploitation dilemma is studied since many decades and is still an unsolved mathematical problem. One of the most used solution to this problem is epsilon greedy policy, where the RL agent will choose a random action instead of the optimal action output from the current policy with probability epsilon. This is followed for searching on a larger area of the state space, and eventually getting a better reward.
Types of Reinforcement learning
- Model-based and Model-free Reinforcement learning: In model-based learning, the agent exploits a previously learned or already available model to accomplish the task at hand whereas in model-free learning, the agent solely relies on some trial-and-error method to learn the criteria for action selection.
- Off-policy vs on-policy Reinforcement learning: In On-policy, the agent uses the deterministic outcomes or samples from a target policy to train an algorithm. But Offpolicy, training is carried out on a distribution of transitions or episodes produced by a different behaviour policy rather than that produced by the target policy.
Important Algorithms
- State–action–reward–state–action (SAARSA)
- Q-Learning
- Deep Q-Network
Deep Learning
Deep Learning is a machine learning technique inspired from the structure and function of the brain called artificial neural networks. This method is proved to be highly efficient for producing very useful informations out of complex data given a large quantity of data. There ability is not limited if we can produce more and more data compared to the limited ability of the conventional algorithms. The core of deep learning according to Andrew Nag is that we now have fast enough computers and enough data to actually train large neural networks. Artificial Neural network (Neural Networks) is an area of machine learning that was around since 1940’s, but only gained a recent upswing [43]. They are fundamentally inspired from biological neural networks in the brain and is in a way mimicking their behaviour. Generally the Neural networks consist of an input, one or many hidden layers, and an output layer. In a N-layer neural network, the N refers to the number of hidden layers plus the output layer. In a feed-forward network, the input layer is not performing any computations and is therefore not counted as a layer. Figure 11 is an example of a three-layer neural network.
METHODS
The work mainly contains three major components which are conducting human walking experiments to collect data, preparing the model and devising appropriate techniques for learning the process and finally testing the results. The first two parts are covered in this chapter in three sections which are as follows:
- Human Experiments: This section contains all details of the human walking experiments conducted for preparing the training dataset for imitation learning.
- Modelling: This section covers all the details of the model including the underlying muscle dynamics.
- Reinforcement Learning: This section covers the details of the RL algorithm used for learning and its implementation.
HUMAN EXPERIMENTS
Acquiring a rich dataset is a desideratum in training a RL agent for imitation learning, so various experiments were conducted to acquire human walking data at different walking speeds. The walking experiments were conducted on a treadmill, the following quantities were acquired from the experiments:
- Joint Kinematics
- Ground Reaction Forces
Walking experiments are conducted on a custom made treadmill available in the laboratory. The Treadmill has KISTLER force sensors embedded on it to measure the ground reaction forces acting on both the legs. In total, it consists of 20 piezo-electric sensors to accurately measure the 3D-force vector and the centre of pressure separately for each side. The treadmill has two levels of force plates. The treadmill drive is capable of driving up-to a speed of 25kmph . The data from force plate are communicate to a host PC with a custom software interface. The data sampling frequency of ground action forces was set to 240Hz.
Motion Capture
To capture joint kinematics during walking, a motion capture set up available in the laboratory
is utilized. The set up consists of 12 High definition Qualisys make cameras placed around
the treadmill and markers placed on all the required joints. The data from all the 12 cameras
were streamed to the host PC using wired communication and is captured using Qualisys
Track Manager(QTM) software. Qualisys generates the joint kinematics using the captured
marker trajectory. The frame rate for the cameras were set at 500Hz. A total of 20 markers were used to capture the joint kinematic data
of ankle, knee, hip, pelvis and trunk. The different marker positions on different body
segments are as follows:
- Foot: SMH(Head of 2nd Metatarsus), CA(Posterior Surface of Calcaneus), FAL(Fibula Apex of Lateral Malleolus) and TAM(Tibia Apex of Medial Malleolus).
- Knee: FLE(Femur Lateral Epicondyle) and FME(Femur Medial Epicondyle)
- Hip: FT(Femur greater Trochanter)
- Pelvis and Trunk: ICT(Ilium Crest Tubercle (Iliac Crest)), LV3(Lumbar Level Vertebrae 3), AC(Acromion) and C7(Cervical Vertebrae 7)
The kinematic marker data captured using the motion capture system is exported as mat files for further processing in MATLAB. The joint position and velocities were low pass filtered and down sampled to 200Hz which is in line with the global timing data created. Then the data is split into individual step data according to the global step timing as described previously. The joint kinematics data consist of the following position and their corresponding velocity data:
- Trunk Centre of Mass 3D translation vector.
- Trunk tilt, list and extension relative to the world frame
- Hip flexion/extension and adduction/abduction.
- Knee flexion/extension
- Ankle Dorsiflexion/plantar flexion
- Position vector of both the foots relative to trunk (Foot position vector)
The final composition the prepared dataset contains 250 walking-steps data at walking speeds in the range of 0.5m/s to 1.3m/s.
MODELLING
The model used in this project is a lower limb human muscle model with 7 segments and 22 muscles. The skeletal-muscle model is based on the human walking model from Seungmoon Song and Hartmut Geyer, but without including the reflex pathways used in their model. The Simulink model developed by H.Geyer and S.Song is already available as open source for using with simulink. But the bottleneck for the Simulink model is the computation time, as in reinforcement learning the agents needs to execute millions of steps to learn a valid policy. Guoping Zhao has transferred the original Simulink model a MuJoCo, excluding the defined reflex pathways in the original model, and this model is being used for this project. The model has Height of 180cm andWeight of 80kg. The model consists of 7 rigid segments connected by 8 internal degrees of freedom(DOFs). In total the model has a total of 14 DOFs freedom (6 global DOFs for trunk and 8 internal DOFs). The physical properties are detailed here in figure 13.
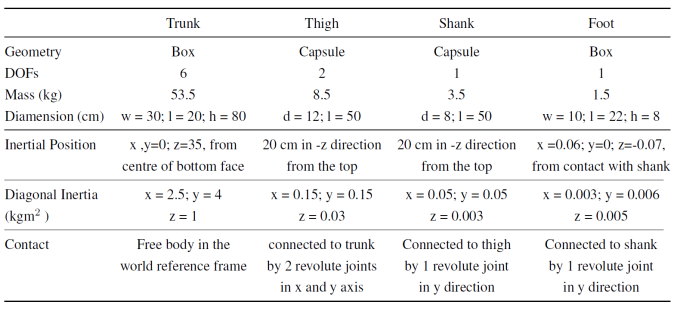
The model is actuated by a total 22 muscle tendon units (MTUs), each leg is actuated by 11 Hill – type MTUs. The muscles included in the model are shown in figure 14. The 11 muscle groupsin each leg are: hip abductors (HAB), hip adductors (HAD), hip flexors(HFL), glutei (GLU), hamstrings (HAM), rectus femoris (REF), vastii(VAS), biceps femoris short head (BFSH), gastrocnemius (GAS), soleus(SOL), and tibialis (TIA). The HAM, REF and GAS are biarticular muscles.The HAB, HAD, HFL, GLU, VAS, BFSH and TIA are monoarticularmuscles. The Muscle Tendon Unit in the model is same as the MTUs from H.Geyer and S.Song, 2015 model, all the 22 MTUs in the model possess a common structure.
Deep Reinforcement learning
Tthe algorithm used for tackling the human locomotion problem in this project is “Proximal Policy Optimization (PPO)” . which is a state of the art deep reinforcement learning algorithm proposed last year (2017) from the researchers in Google-Deepmind. It is proved to match or outperform all the available RL algorithms in the continuous domain but still easy to implement. PPO is proved to train RL policies in challenging environments, like the Roboschool as implemented by Open-AI.
The Clipped Surrogate Objective function allows the PPO algorithm to run multiple epochs of gradient ascent on the samples without causing any extremely large policy updates which is not feasible in the vanilla policy gradient methods. This allows PPO to make use of the samples more effectively which increases the sample efficiency. The PPO is implemented as an actor-critic algorithm, so a learned state value function V (s) is used here. Since here a neural network architecture is used which shares parameters between the policy and value function, the loss function should contain the policy surrogate and a value function error term. Also exploration is very inevitable factor to learn an effective policy, so an entropy bonus term is added to the objective function to encourage exploration.
The final implementation is based on the baselines PPO2 implementation, separate network architecture and hyper-parameters are chosen for both Muscle and Torque model as they differ in the state-action space size and characteristics. Both the policy and value function architecture are defined using neural networks as they are proved to be very promising for processing the rich sensory data. In case of human locomotion problem, the state space is extremely large and complex which demands the use of neural network as the function approximator. The network consists of the input layer which is same as the size of input state vector, in the current scenario it is a single dimensional vector of size n. The middle layers/hidden layers are dense layers of size 512 and 256 respectively, which is found to be optimal with multiple experimentation. The activation function for actor (policy) networks in case of muscle model is Rectified Linear Unit (ReLU) as the required outputs in this case are muscle activation are positive which are in the range of 0 to 1. In case of torque model, the activation function for the actor is hyperbolic tangent function (Tanh) for the first hidden layer and a linear identity unit for the second hidden layer. The linear identity unit was chosen as it was providing better results in this case. But the activation function for the critic (value function) is the hyperbolic tangent function (Tanh). The algorithm is implemented with with W workers running in parallel threads in multiple CPU cored collecting data by acting on the environment. And the collected data of all the workers are use to update the actor and critic policies by training using a single GPU. The pseudo-code of the implemented algorithm is shown below. A gym environment developed by Guoping Zhao is used for the project, the environment named ’Human7s22m-v0’ is implemented in python3 and registered with gym. The environ- ment simulates the 7 segment 22 muscle human model in MuJoCo. For training the torque model the same environment is used by omitting the muscle model.
The input state data needs to be normalized and clipped to the range [-10, 10] to ensure effi- cient learning, here the input state vector and the scalar reward values are normalized using its running mean and standard deviation. In this normalization method firstly the running mean and standard deviation calculated, for this calculation the whole chunk of episode data as one data point. The PPO algorithm is implemented with 40 parallel workers on a 20 core CPU using envi- ronment vectorization implementation from Open-AI baselines parallelization. It is imple- mented as SubprocVecEnv in the baselines and is implemented as a wrapper around the gym environment.
Reward Shaping
Reward function has vital role in reinforcement learning to develop intelligent policies. A lot of effort is spent to shape the reward function to obtain a robust policy. Here the final policy is expected to possess the following characteristics:
- Following the kinematics behaviour from the training data-set
- Executing continues walking without falling down
- Attaining the target walking velocity specified
- Walking with minimum metabolic cost (muscle model)
- Robustness against perturbations on the hip joint (muscle model)
- Generate human like muscle activation (muscle model)
In case of the torque model only first three characteristics are incorporated, but the muscle model incorporates all the six characteristics mentioned above. In order to develop a policy with all these characteristics, it is necessary to have a reward function which can guide the policies to these goals. Generally, reward function is the only medium which can convey the desired behaviour to the policy by rewarding it with bonus or penalties. There is no specific standardized methodology to shape reward function to achieve different goals, so it requires a lot of brainstorming along with trial and error methodology to shape a good reward function. The physical insights of the model-environment interaction is very important to shape a reward function, as this helps us not only to decide various components in the reward function but most importantly to debug model behaviour to improve the reward function. In the current project the reward function for the muscle model contains terms which encourage following the trajectory, staying alive (not collapsing from normal walking), attaining and maintaining the target velocity and reducing the metabolic cost. The final reward function looks as follows:
The reward function for the muscle and torque model contain terms which encourage imitating the kinematic trajectory, continuous stable walking, attaining a target velocity. An additional metabolic cost reward term is included for the muscle model, but the torque model is learned without using any torque minimization term. \begin{equation} r = w_{l}r_{l} + w_{k}r_{k} + w_{m}r_{m} + w_{v}r_{v} \end{equation} where \(r\) is the reward, \(r_{l}\) is the life bonus, \(r_{k}\) is the kinematic behavior bonus, \(r_{m}\) is the metabolic bonus and \(r_{v}\) is the target velocity bonus. \(w_{l}\)=1, \(w_{k}\)=4, \(w_{m}\)=4, \(w_{v}\)=1 are the weights of \(r_{l}\), \(r_{k}\), \(r_{m}\) and \(r_{v}\), respectively. All these individual bonus is between 0 and 1. The total reward, \(r\) is in the range from 0 to 10. The life bonous \(r_{l}\) denotes the reward for walking without falling. The falling condition occur when the pelvis vertical position is out of the range [0.8, 1.4]\,m. The \(r_{k}\) term defines the reward for imitating the desired trajectory. Individual position and velocity errors between the model and the experimental data are calculated for each sampling step. These errors are:
Foot position vector error \(e_{fp}\) which denotes the squared difference between the foot position vector of the model and the reference human trajectory data. \begin{equation} e_{fp} = [ c ( s_{fp}(t) - \bar{s}_{fp}( t ) ) ] ^ { 2 } \end{equation} Here, \(s_{fp}(t)\) and \(\bar{s}_{fp}(t)\) are the foot position vector of the model and the reference data respectively at time t and the scaling coefficient, \(c\)=30.
Pelvis COM position error \(e_{pp}\) which denotes the squared difference between the pelvis COM position vector of the model and the reference data. \begin{equation} e_{pp} = [ c ( s_{pp}(t) - \bar{s}_{pp}( t ) ) ] ^ { 2 } \end{equation} Here, \(s_{pp}(t)\) and \(\bar{s}_{pp}(t)\) are the pelvis COM position vector of the model and the reference data respectively at time t and \(c\)=20. Pelvis COM velocity error \(e_{pv}\) which denotes the squared difference between the pelvis COM velocity vector of the model and the reference data. \begin{equation} e_{pv} = c[ s_{pv}(t) - \bar{s}_{pv}( t ) ] ^ { 2 } \end{equation} Here, \(s_{pv}(t)\) and \(\bar{s}_{pv}(t)\) are the pelvis COM velocity vector of the model and the reference data respectively at time t and \(c\)=2. Joint angular position error \(e_{ap}\) which denotes the squared difference between all the joint angles of the model and the reference data. \begin{equation} e_{ap} = [ c ( \theta_{ap}(t) - \bar{\theta}_{ap}( t ) ) ] ^ { 2 } \end{equation} Here, \(\theta_{ap}(t)\) and \(\bar{\theta}_{ap}(t)\) are the array of all the joint angles of the model and the reference data respectively at time t and \(c\)=12. Joint angular velocity error \(e_{av}\) which denotes the squared difference between all the joint angular velocities of the model and the reference data. \begin{equation} e_{av} = [ c ( \theta_{av}(t) - \bar{\theta}_{av}( t ) ) ] ^ { 2 } \end{equation} Here, \(\theta_{av}(t)\) and \(\bar{\theta}_{av}(t)\) are the array of all the joint angular velocities of the model and the reference data respectively at time t and \(c\)=0.1.
All these individual errors are concatenated to form a single error vector, \(E\) as follows: \begin{equation} E = [e_{fp}, e_{pp} ,e_{pv}, e_{ap}, e_{av}] \end{equation} \(E\) is converted to its negative exponential and the resulting terms are summed up to get a scalar value \(T\): \begin{equation} T = \operatorname { sum } \left[ \mathrm { e } ^ { - E } \right] \end{equation} The \(r_{k}\) term denotes how large is the \(T\) value compared to the limiting value of 28. It is computed as follows \begin{equation} r_{k} = \frac{T - T_{\text{limit}}} {T_{max} - T_{limit} } \quad \text{where}\ T_{limit} = 28 \text { , }\ T_{\max} = 35 \end{equation}
The value of \(r_{k}\) is between 0 to 1, where 1 denotes an exact imitation of the joint trajectory and 0 corresponds a maximum allowed deviation defined by \(T_{limit}\). The $T_{limit}$ is also used as the ES criterion. In other words, the ES will be triggered if $T<T_{limit}$.
The metabolic rate \(p\) for the musculoskeletal model is estimated based on the muscle states according to Alexander’s work \cite{Reference76}.
The metabolic energy over a sampling step is converted to a value between 0 to 1 by taking the negative exponential with a coefficient of 1/30. The value of 1/30 is chosen by monitoring the range of \(p\) during training. The calculation of \(r_{m}\) as follows: \begin{equation} r_{m} = e ^ { {-p}\left/{30} \right.} \end{equation}
The \(r_{v}\) term is a function of the difference between the running mean of the experimental walking speed \(\bar{v}_{p}\) and the running mean of the model walking speed \(v_{p}\).
\begin{equation} r_{v} = \frac { \sum ( e ^ {e_{v}}) }{ 3 } \quad \text { where} \; e_{v} = c [\bar{v}_{p} -v_{p}]^{2} \end{equation} The coefficient \(c=50\).
Results
KINEMATIC IMITATION BEHAVIOUR
In this session the both the muscle and torque model’s quality of imitating the human sub- ject’s lower-limb joint trajectory during normal walking is analyzed and compared. The reward function for both the models were shaped to encourage the policy to follow the real trajectories closely, but not necessarily to be pin-point accurate. The kinematic results of both the models are analyzed for three different speeds of 0.6, 0.9 and 1.2ms−1. In the results of both the muscle and torque models in comparison to the experimental data from the human is plotted in the figures 4.2 to 4.7. The results plotted here are the mean trajectory of steady walking with a fixed target speed over 100 steps of walking. The trajectory is plotted against the percentage of gait cycle (touch-down to touch-down) for both the left and right legs. The mean value of the trajectory is calculated by averaging the individual trajectories of walking steps which are interpolated to a fixed length sequence 100 data points. The model’s closeness to the experimental data is quantified by calculating the cross-correlation value between them, which is denoted as R in the plots. The kinematic results are plotted for pelvis tilt, pelvis list, hip adduction/abduction, hip flexion/extension, knee flexion/extension, ankle dorsiflexion/plantar flexion trajectories. The Rright and Rleft denotes the cross cor- relation values(R) for right and left leg joints respectively. Pelvis rotation trajectory is not plotted as it is set to be stationary in the reference trajectory as there is no other rotational degree of freedom for any other joints. In the plots the model output is represented with continuous lines and the human data is represented using dashed lines. Figures 4.2 to 4.4 are from the muscle model and figures 4.5 to 4.7 are from the torque model. The muscle and torque models are tested with randomly chosen reference trajectories de- pending upon the initial conditions providing better results. So the reference trajectories of both the models in the plots should not be compared. The human subject data used here has high asymmetries, in the frontal movement of the hip joints across all three walking speeds and in knee angle at very slow walking speed (0.6ms−1). The results show that both the models could successfully capture these complex asymmetries across all the speeds. In all the trajectories a delay is evident between the human trajectory and the model trajectory. Although pelvis trajectory seems to deviate considerably from the human trajectory, the magnitude of deviation is very less as seen in the plots. In most cases the trajectory is followed very closely in the beginning 5% of the gait cycle.


MUSCLE DYNAMICS
The muscle model is trained to reproduce human-like muscle activations through stimulation clipping and optimizing for minimum metabolic cost. The stimulation clipping is based on the reference muscle activation patterns provided in the figure 17 But it is found to be very hard for the model to closely adapt the human-like muscle activation patterns. Also the muscle patterns used for clipping the stimulations were not from the same subject whose kinematic data is used. So I am not sure about how realistic and fair is it comparing the model’s result with the with reference muscle activation data. Since there is no other valid data available to me currently I am going on to make, may be an unfair comparison here about the model’s muscle dynamics with the human muscle dynamics. These results shows that the muscle activation patterns from the model are not very close to the reference human activation data. A better comparison could be made by comparing the model and the right subject whose kinematics data was used for learning. Still there could be limitations from the model, especially the foot contact model which needs to improved to make it more human-like. This solution could be considered as one for the solution in the pool of local minimum solutions for the energy efficiency.
PERTURBATION RESPONSE

Robustness to perturbations is an important aspect of the human walking model. It is ideal to learn a model that can reproduce human behaviour/response to the external perturbation, which is an important aspect in case of exoskeletons. But here the perturbation are added to the system only in the hip joints in the sagittal plane by exerting random torque values in the range ±5Nm as detailed in chapter 2. This behaviour is only incorporated in the muscle model. The model is tested using perturbations from 0 to ±350Nm on the hip joints for 50ms at the the beginning of the gait cycle. The figure 18 shows the number of steps executed by the model for different values of the torques applied on the left hip flexion joint at the start of left leg touch-down for a duration of 50sec for a walking speed of 0.9ms−1 and similarly in the right hip flexion joint for right leg take off. The perturbation torques are applied only to one joint at a time here in the tests. The perturbation characteristics exhibited by the model is highly interesting as it is in con- trast to the general expectation that the model performance to deteriorate with the increasing perturbation torques. Here for both touch-down and take-off conditions the perturbation behaviour is highly unexpected at looks random except for the obvious conditions like the performance drops faster when the high extension torques are applied to the take off leg.
GROUND REACTION FORCE (GRF)
The ground reaction force profile of the model is analyzed comparing it with the human ground reaction force collected through the experiment. The figure 19 shows the ground reaction force data of the model and human plotted for one complete gait cycle of the gait cycle at a walking speed of 1.2m/s. The individual ground reaction force profiles in case of model have higher level of disturbance. The cross cor- relation value of between the mean ground reaction force of the model and the human is 0.98.
RL LEARNING CURVES
The learning curves are very important aspect in solving any reinforcement learning problem. Here the learning curves are monitored continuously to asses the progress and to tune the hyperparameters. Two sample learning curves for the muscle model training and torque model training are shown in figure 20. It is clear that the muscle model is outperforming the torque model completely in the learning efficiency. Here when the muscle model achieves a mean total return of 1688 after 10 million timesteps where as the torque model reaches a mean total return of 1497 after 27.65 million timesteps.
DISCUSSION and CONCLUSIONS
DISCUSSION The kinematic imitation results analyzed for both the muscle model as well as in the torque model.The Model here is not following the trajectory with pin-point accuracy as it is not demanded here. The objective here is to produce a general human walking behavior over various walking speeds and this general behaviour has a variance in the subject itself. So it is not desirable for the model to approximate each of the trajectory exactly , but it is desirable to learn the general pattern rather. The learned model is able to closely follow the position trajectories. On comparison with the with the results at 1.2ms−1 form H.Geyer and S.Song, our model produces an R value of 0.832 and 0.946 for the left and right legs respectively compared to 0.54 in their model in reproducing the hip adduction/abduction movement. Also for ankle(frontal plane) movements, our model has a R value of 0.96 compared to 0.46 in their model at 1.2ms−1. These could be seen as considerable improvements also considering the fact that our model could also learn the asymmetries of the human subject very closely which is visible in the hip movement in the frontal plane and the pelvis tilt movement. But in case of the reference model discussed here it is modelling a symmetrical/ideal human gait. But the performance on following the velocity trajectory is not very close to the human velocities. This could be because of setting very low weightage for the velocity trajectory error component compared to the position error in the reward function. It it advisable to try to have various settings for the relative weightages of position and velocity error components to find an optimum solution, but it is not yet properly investigated here because of the time constraint. Considering the position in all the trajectories a delay is evident between the human trajectory and the model trajectory. This could be because of the relaxed constraints on the imitation learning.
Here the model’s stimulation inputs are clipped based on the reference muscle activations from s.song and H.Geyer which are considered to be an ideal human pattern without any asymmetries at a normal walking speed of 1.2ms−1. In their work, the muscle activation pattern correlation between the model and the human is much better than the results from this thesis. On comparing the results of their model and our model it can be seen that the HAB, HAD, HFL, GLU, VAS, SOL and TA muscles have a good correlation. But only HFL, GLU, VAS, SOL and TA muscles in their work has a cross correlation value more than 0.8. In-spite of close similarities between the two models in 7 muscle groups it has to be noted that there is a huge difference in remaining muscles except for HAM, which are REF(RF), BFSH and GAS. The BFSH and RF has very high activation levels in our model but has very low activation levels in their model and vice-versa in GAS. The difference in GAS has to be noted very importantly as this lower activation of GAS could be responsible for higher activations from BFSH as these muscles together are responsible for knee flexion. Low level of maximum force of the BFSH muscle group explains its higher activation levels,as needs to generate enough torque for the knee flexion. Similarly the higher activation levels in RF(REF) muscle group in our model could be a result of very low activation from HAM muscle group as both of them aid hip extension. It is not exactly clear on how exactly to train the model to achieve human-like muscle activa- tion efficiently and what are the limitations from the model, algorithm or any other sources. But primarily as discussed before it is not fair to approximate this general pattern to a subject with clear asymmetries as here the model is trying to mimic the kinematics of a particular subject. May be it possible to achieve much better results using the activation patterns of this particular subject, unfortunately this method has not been yet tried out yet because of the time constraint. But it was decided to still assume the muscle model trained to optimize for the ref- erence muscle pattern as the final outcome of the thesis in-spite of it’s inferior performance. This is because it is one of the important factor to bring the model closer to the human which is the main objective of the whole work. It has to be noted that the muscle model without any stimulation clipping offers much more robust and accurate kinematic behavior, but in the expense unrealistic muscle activation with many co-activation and higher metabolic cost. But instead of using the reference muscle activation pattern from the literature, it is more fair to use the original subject’s muscle activation pattern. The ground reaction force profile is an important factor in modelling human locomotion [31, 34, 38]. This is well visible in the learning procedure as the ground reaction force data feedback has higher weightage in the final policy. When the delay was introduced to the ground reaction force it has considerably reduced the performance of the final learned model. As it is visible from the results that the ground reaction force data is not very ideal and has high oscillation, but still the mean value GRF has a high correlation with human GRF data with an R value of 0.98. Improvement in the foot model might have a higher impact on the ground reaction force profile and should be able increase the model performance considerably. In the new version of MuJoCo released, MuJoCo 2.0 has provisions for soft material modelling and this could be adapted to improve the foot model. The 3 section foot models as in OpenSim models also could be adapted as this gives foot the flexibility of smooth touch-down, roll over and push- off rather than a rigid body with four contact points as in here. Also the foot touch-down of the model is not very ideal as there are many cases of flat foot contacts and top touch-down instead of normal heel touch-down. This is because of the summed up trajectory deviation of all the angles in the sagittal plane.
The perturbation behaviour is much unexpected and is always supposed to happen with a neural network function approximator. But this character could not be thought as a result of the perturbation training as it was only trained for perturbation values in the range of ±5Nm. In results discussed in chapter 3, the model is tested with an initial perturbation of ±350Nm and the behaviour is similar in the trained range of ±5Nm also. This could be a result of the policy learned and the passive dynamics of the muscles which is making it capable of stabilizing even very high perturbation toques such as 230Nm. This could be seen as a possibility to learn very complex perturbation behaviours of the human being. Clearly all the perturbations are adversely affecting the performance of the model. Also here it is possible to produce much robust muscle model when trained without any stimulation clipping. But here the results are only discussed for the muscle model trained with stimulation clipping. A better training method with an improved model could produce a more robust model.\
The metabolic cost is used here to optimize the model gait based on energy efficiency. Here the metabolics is implemented using the work of Alexander, and this value is included in reward function with a weightage 40% to optimize the model for energy efficiency. This implementation has has considerably reduced the metabolic cost of the model, but it didn’t help in providing very realistic muscle activation without using the stimulation clipping pro- cedure. It could be because the model is getting trapped in one of the pool of local minimum solutions for energy efficiency, as the the human gait is regarded to be optimized for energy efficiency. In the initial stages of this project, a rough study was conducted find the relation between the EMG data and the metabolics. A deep neural network was used to approximate the relationship between the EMG and metabolic cost. So, instead of the theoretical method used to calculate the metabolic cost , such a deep neural network based approximator could be used to get more accurate estimate of the metabolic cost in the model. Also mechanisms needs to be devised to to identify if the policy is stuck in a local minimum, if so how to guide it out of it. There weren’t much efforts in this respect in the current work because of time constraints.
It is understood that the muscle based system could take advantage of its passive dynamics to learn a robust policy. Here in the kinematic results although both the models are producing similar results, but clearly the torque model’s pelvis trajectory is deviating an lot form the original trajectory and becoming unstable at higher velocities. There are few important aspects, which is not evident in the kinematic data plotted before. The major differences between the muscle models and torque model is as follows:
- Training effort: The training effort in the Torque model is much higher than the muscle model, in the current scenario the toque model takes around 5 times the training steps compared to the muscle model. On comparing the time taken for training the torque model takes at least twice the training time for muscle model to produce similar results.
- Robustness: The final policy learned by the muscle model is much more robust com- pared to the torque model. Also the muscle model is capable of handling much lower control frequency compared to the torque model. Here the torque model is trained with perturbations as the learning is quite slow and might need higher control frequency to learn a good policy.
- Performance: Also the performance is reproducing the kinematic behaviour is similar another important factor to be noted is how far the model is able to continuously walk without failing/collapsing. In a naive comparison; in case of muscle model capable of executing over 100 steps the torque model it is around 50 steps.
The RL learning curve shows a fast a increase in learning in both torque and muscle models initially and then gradually becoming slower with time. At the same time the muscle based is much superior to torque based model in learning. Here when the muscle model achieves a mean total return of 1688 after 10 million timesteps where as the torque model reaches a mean total return of 1497 after 27.65 million timesteps. Which could be seen as around three-fold difference in the timesteps required, but still then the steady state episode reward achieved by the torque model is only 88% of the steady state episode reward achieved by the muscle model. This also established the superiority of muscle model over torque model. With longer training the reward further increases, but at a very slow pace. This has to be addressed to achieve much higher rewards by choosing better hyperparameters.
CONCLUSION
As a final conclusion of the thesis outcome with respect to the objectives is that, the objectives were partially achieved within the limited time frame of the project. The final outcome of this thesis could be stated as: „Developed a lower limb muscle model capable of executing human-like 3D walking based on deep reinforcement learning with the following characteristics:“
- Waking at a specified target velocity: Model’s capability to walk at a pre-specified walking velocity is not achieved accurately, but model can execute this character with an error bound of 0.1m/s.
- Human-Like behaviour: The human-like behaviour is attempted to achieve at all the levels as stated in the objective, the final outcomes of various objectives in achieving human-like behaviours can be concluded as follows:
- At the kinematic level the joint angles except for the pelvis angles were closely matched and also could capture the asymmetries in the kinematics of the subject.
- At the muscular level it has been tried to achieve human-like muscle activation pattern, but the results were not ideal compared to the reference patterns used. But this optimization is not conducted with the muscle activation patterns of the same subject whose kinematic data is used, so this capability of the model is completely tested.
- Regarding the ground reaction force (GRF) patterns generated by the model is not exactly like the human ground reaction force pattern and need to addressed with improvements in the model.
- Optimizing metabolic cost/energy cost has been implemented and observed and the final solution is possibly one of the pool of local minimum solution. But no- ticeably this implementation helped in removing most of the muscle co-activations to improve the energy efficiency.
- Robustnessofthemodelistestedwithapplyingperturbationsonthehip±300Nm and the model is able to walk stably up-to 20 steps even at higher perturbations up-to ±200Nm. But the perturbation behaviour is highly random and not well understood, this needs to addressed.
- Themodelfailsatacceleration/decelerationbehaviours,generallythemodellosses stability on trying to accelerate to a different target velocity from the current walking velocity. This is basically due to the lack of enough acceleration/deceleration data in the dataset
During the course of this thesis, idea of using deep reinforcement learning to model the complex human walking/locomotion behaviour is well tested. Along with the final model and other results and observations it could be argued to be the better way to model the human locomotion behaviour. On an optimistic yet realistic note it can be concluded that, hand in hand with deep reinforcement learning, having a general human model is quite achievable. Also the torque based and muscle based models methods are considered on the aspects of kinematic imitation and it was clear that the muscle based modelling is the right way over the torque based modelling.
Literatur
Hochmuth, G. (1967). Biomechanik sportlicher Bewegungen. Frankfurt (a. M.): Limpert-Verlag GmbH.
Desmond, N. Layton, J. Bentley, F. H. Boot, J. Borg, B. M. Dhungana, P. Gallagher, L. Gitlow, R. J. Gowran, N. Groce et al., “Assistive technology and people: a position paper from the first global research, innovation and education on assistive technology (great) summit,” Disability and Rehabilitation: Assistive Technology, vol. 13, no. 5, pp. 437–444, 2018.
H. Geyer and A. Seyfarth, “Neuromuscular control models of human locomotion,” Humanoid Robotics: A Reference, pp. 979–1007, 2019.
J. Zhang, P. Fiers, K. A. Witte, R. W. Jackson, K. L. Poggensee,
C. G. Atkeson, and S. H. Collins, “Human-in-the-loop optimization of exoskeleton assistance during walking,” Science, vol. 356, no. 6344, pp. 1280–1284, 2017.
Y. Ding, M. Kim, S. Kuindersma, and C. J. Walsh, “Human-in-the- loop optimization of hip assistance with a soft exosuit during walking,” Science Robotics, vol. 3, no. 15, p. eaar5438, 2018.
S. Song and H. Geyer, “A neural circuitry that emphasizes spinal feedback generates diverse behaviours of human locomotion,” The Journal of physiology, vol. 593, no. 16, pp. 3493–3511, 2015.
X. B. Peng, P. Abbeel, S. Levine, and M. van de Panne, “Deepmimic: Example-guided deep reinforcement learning of physics-based char- acter skills,” arXiv preprint arXiv:1804.02717, 2018.
X. B. Peng, G. Berseth, K. Yin, and M. Van De Panne, “Deeploco: Dynamic locomotion skills using hierarchical deep reinforcement learning,” ACM Transactions on Graphics (TOG), vol. 36, no. 4, p. 41, 2017.
X. B. Peng and M. van de Panne, “Learning locomotion skills using deeprl: Does the choice of action space matter?” in Proceedings of the ACM SIGGRAPH/Eurographics Symposium on Computer Animation. ACM, 2017, p. 12.
H. S. Chang, M. C. Fu, J. Hu, and S. I. Marcus, “Google deep mind’s alphago,” OR/MS Today, vol. 43, no. 5, pp. 24–29, 2016.
J. Schulman, F. Wolski, P. Dhariwal, A. Radford, and O. Klimov, “Proximal policy optimization algorithms,” arXiv preprint arXiv:1707.06347, 2017.
J. Schulman, S. Levine, P. Abbeel, M. Jordan, and P. Moritz, “Trust region policy optimization,” in International Conference on Machine Learning, 2015, pp. 1889–1897.
T. P. Lillicrap, J. J. Hunt, A. Pritzel, N. Heess, T. Erez, Y. Tassa, D. Silver, and D. Wierstra, “Continuous control with deep reinforce- ment learning,” arXiv preprint arXiv:1509.02971, 2015.
V. Mnih, A. P. Badia, M. Mirza, A. Graves, T. Lillicrap, T. Harley, D. Silver, and K. Kavukcuoglu, “Asynchronous methods for deep rein- forcement learning,” in International conference on machine learning, 2016, pp. 1928–1937.
Z.Wang,V.Bapst,N.Heess,V.Mnih,R.Munos,K.Kavukcuoglu,and N. de Freitas, “Sample efficient actor-critic with experience replay,” arXiv preprint arXiv:1611.01224, 2016.
P.Dhariwal,C.Hesse,O.Klimov,A.Nichol,M.Plappert,A.Radford, J. Schulman, S. Sidor, Y. Wu, and P. Zhokhov, “Openai baselines,” https://github.com/openai/baselines, 2017.
R. M. Alexander, “Optimum muscle design for oscillatory move- ments,” Journal of theoretical Biology, vol. 184, no. 3, pp. 253–259, 1997.
A. S. Anand, “Deep-rl of individual walking gait,” https://www.youtube.com/watch?v=bEzy4ZuFeo0, accessed: 2019- 02-26.
M. Y. Zarrugh, F. N. Todd, and H. J. Ralston, “Optimization of energy expenditure during level walking,” European Journal of Applied Physiology and Occupational Physiology, vol. 33, no. 4, pp. 293–306, Dec 1974. [Online]. Available: https://doi.org/10.1007/BF00430237
K. Hirai, M. Hirose, Y. Haikawa, and T. Takenaka, “The develop- ment of honda humanoid robot,” in Robotics and Automation, 1998. Proceedings. 1998 IEEE International Conference on, vol. 2. IEEE, 1998, pp. 1321–1326.
J. P. Hunter, R. N. Marshall, and P. J. McNair, “Relationships between ground reaction force impulse and kinematics of sprint-running accel- eration,” Journal of applied biomechanics, vol. 21, no. 1, pp. 31–43, 2005.
T. S. Keller, A. Weisberger, J. Ray, S. Hasan, R. Shiavi, and D. Spen- gler, “Relationship between vertical ground reaction force and speed during walking, slow jogging, and running,” Clinical biomechanics, vol. 11, no. 5, pp. 253–259, 1996.
A. Cruz Ruiz, C. Pontonnier, N. Pronost, and G. Dumont, “Muscle- based control for character animation,” in Computer Graphics Forum, vol. 36, no. 6. Wiley Online Library, 2017, pp. 122–147.
J. Schröder, K. Kawamura, T. Gockel, and R. Dillmann, “Improved control of a humanoid arm driven by pneumatic actuators,” Proceed- ings of Humanoids 2003, 2003.
T. Komura, Y. Shinagawa, and T. L. Kunii, “A muscle-based feed- forward controller of the human body,” in Computer Graphics Forum, vol. 16, no. 3. Wiley Online Library, 1997, pp. C165–C176.
X. Shen, “Nonlinear model-based control of pneumatic artificial muscle servo systems,” Control Engineering Practice, vol. 18, no. 3, pp. 311–317, 2010.

















