Dies ist eine alte Version des Dokuments!
Inhaltsverzeichnis
Simulation02
| Thema | Simulation |
|---|---|
| Veranstaltung | ADP Laufrobotik |
| Semester | WS 2012/13 |
| Namen | Burbach, J.-N.; Erler, P.; Hoitz, F.; Stuhlenmiller, F.; Xiaoguang, Z.; Zimmermann, C.; Zwetsch, F. |
| Bearbeitungsdauer | 60 min |
| Author/Verantwortlich | Philipp Erler |
Das Hopper-Modell
Abbildung 1 zeigt das Hopper-Modell mit eine Freischnitt-Skizze. Die Kinematik, die die Masse <latex>m_2</latex> über den Muskel hält wird hier nicht dargestellt, sondern die Masse m2 direkt an die Feder SEE drangeheftet. Neben dem Fuß der durch die Masse <latex>m_1</latex>, einer Feder mit der Steifigkeit <latex>k_1</latex> und eine Dämpfung mit <latex>b_1</latex> abgebildet wird, sind an den Verbindungsstellen der Elemente bzw. für jede Koordinate Massen (<latex>m_3</latex> und <latex>m_4</latex>) eingefügt worden. Diese dienen als Platzhalter und können später verwendet werden, wenn die einzelnen Komponenten des realen Aufbaus ausgelegt sind und somit auch deren Massen. Als Zwischenschritt zu diesem Modell wurde ein Hopper-Modell ohne <latex>m_3</latex> und <latex>m_4</latex> entwickelt. Da sich durch das Modell mit den Massen nahezu das gleiche Systemverhalten einstellt, wenn für diese sehr geringe Werte verwendet werden, wird an dieser Stelle nicht weiter auf das „Zwischen-Modell“ eingegangen. Da in der Realität jede Feder eine steifigkeitsproportionale Dämpfung besitzt, wird an deren Stellen eine Dämpfung in Höhe von b = 0.02k vorgesehen. Im Folgenden werden die aus den Kräftegleichgewichten und Zwangsbedingungen hergeleiteten Gleichungen vollzählig aufgestellt. Aus dem Kräftesatz an den 4 Massen ergeben sich folgende Gleichungen:

(19 - 22)
Diese werden nach der Koordinate aufgelöst und in Simulink implementiert. Für jede Koordinatenberechnung wird ein Subsystem erstellt. Desweiteren ergeben sich durch die Dämpfer und Federn folgende zum Teil schon bekannte Koppelgleichungen (Berechnung <latex>d_{PDE}</latex> (<latex>F_{CE}</latex>) siehe (4.3):
(23, 24)
<imgcaption image9 |Hopper-Modell mit Freischnitt Skizze> </imgcaption>
</imgcaption>
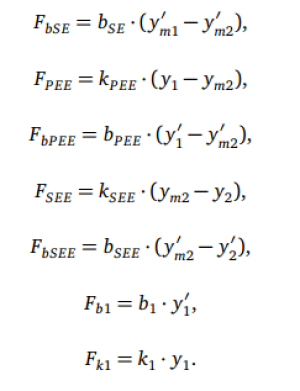
(25 - 31)
Die Steifigkeit k1Validierung
Zuerst werden nochmals die statischen Auslenkungen an den drei Koordinaten berechnet und mit den
Ausgangssignalen der Simulation verglichen.
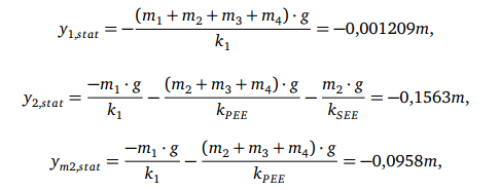
(32 - 34)
Wie in Abbildung 2 zu sehen ist, stimmen die berechneten Werten mit denen der Simulation überein. Die geringen Abweichungen ab der dritten Nachkommastelle sind auf numerische Fehler und die nicht vollständig abgeklungene Schwingung zurückzuführen. <imgcaption image10 |Statische Auslenkung des Hopper-Modells. Verwendete Parameter siehe Tabelle A.3> </imgcaption>
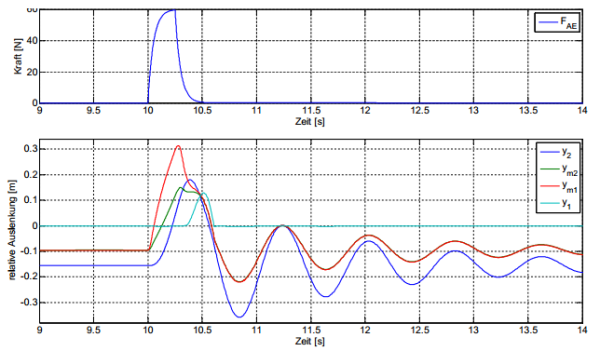
Neben den statischen Auslenkungen wird auch das Sprungverhalten betrachtet, um abzuschätzen
ob das dynamische Verhalten plausibel ist. In Abbildung 3 ist der Verlauf der Kraft <latex>F_{AE}</latex> und der zugehörige Verlauf der Koordinaten dargestellt. Man sieht deutlich, dass die Koordinate <latex>y_{m1}</latex>, an der die
<imgcaption image11 |Dynamisches Verhalten Hopper-Modell. Verwendete Parameter siehe Tabelle A.3>
</imgcaption>
Neben den statischen Auslenkungen wird auch das Sprungverhalten betrachtet, um abzuschätzen
ob das dynamische Verhalten plausibel ist. In Abbildung 3 ist der Verlauf der Kraft <latex>F_{AE}</latex> und der zugehörige Verlauf der Koordinaten dargestellt. Man sieht deutlich, dass die Koordinate <latex>y_{m1}</latex>, an der die
<imgcaption image11 |Dynamisches Verhalten Hopper-Modell. Verwendete Parameter siehe Tabelle A.3>
 </imgcaption>
Kraft <latex>F_{AE}</latex> die größte Auslenkung erfährt, gefolgt von einer Auslenkung von <latex>y_{m2}</latex>, auf welche wiederum
eine Auslenkung von <latex>y_2</latex> folgt. <latex>F_1</latex> wird zu dieser Phase aufgrund der hohen Steifigkeit lediglich
leicht abgesenkt. Nach einer Aktivierung von <latex>t_{act} = 0.25s</latex> ist die Maximalkraft <latex>F_{AE}</latex> erreicht. Die Dauer
der Aktivierung <latex>t_{act}</latex> wurde willkürlich festgelegt. Durch die Verzögerung von <latex>t_{verzoeg} = 50ms</latex>
fällt die Kraft nicht sofort auf Null herab. Nach diesem Zeitpunkt erreicht <latex>y_{m1}</latex> die maximale Auslenkung
und kurz darauf <latex>y_{m2}</latex> ebenfalls. <latex>y_2</latex> steigt weiter an aufgrund der in der Masse <latex>m_2</latex> gespeicherten
kinetischen Energie. Diese kinetische Energie wird von der Feder PEE abgestützt und auf die Masse
<latex>m_1</latex> übertragen. Daher folgt kurz nach dem Erreichen der maximalen Auslenkung von <latex>y_2</latex> ein starker
Anstieg von <latex>y_1</latex>. Die unter kritisch gedämpften Koordinaten <latex>y_{m1}</latex>, <latex>y_{m2}</latex> und <latex>y_2</latex> führen daraufhin eine
der Eigendynamik des Systems entsprechenden Schwingung aus. Die Frequenz dieser Schwingung
wird im Folgenden näher betrachtet. Die Verläufe werden mit weiteren Parameter Kombinationen
betrachtet, um Erkenntnisse über den Einfluss einzelner Parameter zu erhalten und auf Korrektheit zu
überprüfen. Diese werde an dieser Stelle jedoch nicht weiter erläutert.
Die Struktur des Hoppers ist an dieser Stelle vollständig und weißt keine Fehler auf. Daher wird mit
diesem Modell eine vorläufige Parametrierung durchgeführt. Dazu wird eine Auslegungsmethode
verwendet, die in Rücksprache mit Häufle festgelegt wurde: Die Federsteifigkeit des SEE wird so
gewählt, dass die Eigenfrequenz der Masse <latex>m_2</latex> der Frequenz entspricht, mit der gehüpft wird. Als
„Hüpf-Frequenz“ wird 2Hz festgelegt, diese liegt unter der maximalen Hüpf-Frequenz des Marco
Hoppers. Daraus ergibt sich für die Steifigkeit
</imgcaption>
Kraft <latex>F_{AE}</latex> die größte Auslenkung erfährt, gefolgt von einer Auslenkung von <latex>y_{m2}</latex>, auf welche wiederum
eine Auslenkung von <latex>y_2</latex> folgt. <latex>F_1</latex> wird zu dieser Phase aufgrund der hohen Steifigkeit lediglich
leicht abgesenkt. Nach einer Aktivierung von <latex>t_{act} = 0.25s</latex> ist die Maximalkraft <latex>F_{AE}</latex> erreicht. Die Dauer
der Aktivierung <latex>t_{act}</latex> wurde willkürlich festgelegt. Durch die Verzögerung von <latex>t_{verzoeg} = 50ms</latex>
fällt die Kraft nicht sofort auf Null herab. Nach diesem Zeitpunkt erreicht <latex>y_{m1}</latex> die maximale Auslenkung
und kurz darauf <latex>y_{m2}</latex> ebenfalls. <latex>y_2</latex> steigt weiter an aufgrund der in der Masse <latex>m_2</latex> gespeicherten
kinetischen Energie. Diese kinetische Energie wird von der Feder PEE abgestützt und auf die Masse
<latex>m_1</latex> übertragen. Daher folgt kurz nach dem Erreichen der maximalen Auslenkung von <latex>y_2</latex> ein starker
Anstieg von <latex>y_1</latex>. Die unter kritisch gedämpften Koordinaten <latex>y_{m1}</latex>, <latex>y_{m2}</latex> und <latex>y_2</latex> führen daraufhin eine
der Eigendynamik des Systems entsprechenden Schwingung aus. Die Frequenz dieser Schwingung
wird im Folgenden näher betrachtet. Die Verläufe werden mit weiteren Parameter Kombinationen
betrachtet, um Erkenntnisse über den Einfluss einzelner Parameter zu erhalten und auf Korrektheit zu
überprüfen. Diese werde an dieser Stelle jedoch nicht weiter erläutert.
Die Struktur des Hoppers ist an dieser Stelle vollständig und weißt keine Fehler auf. Daher wird mit
diesem Modell eine vorläufige Parametrierung durchgeführt. Dazu wird eine Auslegungsmethode
verwendet, die in Rücksprache mit Häufle festgelegt wurde: Die Federsteifigkeit des SEE wird so
gewählt, dass die Eigenfrequenz der Masse <latex>m_2</latex> der Frequenz entspricht, mit der gehüpft wird. Als
„Hüpf-Frequenz“ wird 2Hz festgelegt, diese liegt unter der maximalen Hüpf-Frequenz des Marco
Hoppers. Daraus ergibt sich für die Steifigkeit

(35)
Da für die Steifigkeiten ein runder Wert günstig ist und aufgrund kleinerer Auslenkungen die Steifigkeit Richtung höherer Werte tendiert, wird <latex>k_{SEE} = 230/fac{N}{m}</latex> festgelegt. Die Steifigkeit <latex>k_{PEE}</latex> soll nach Aussage von Häufle möglichst gering gewählt werden und deutlich kleiner als <latex>k_{SEE}</latex>. Daraus ergibt sich jedoch das Problem, dass die Differenz der Auslenkungen y1
(36)
<imgcaption image12 |Leistungsdichtespektrum der Koordinate y2 des Hopper-Modells. Verwendete Parameter siehe Tabelle A.3, Federdämpfungen auf 0 gesetzt>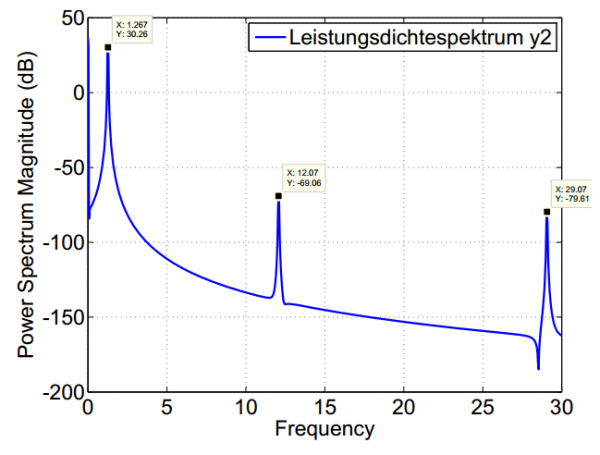 </imgcaption>
Der Wert <latex>f_{y2,approx}</latex> stimmt fast mit der niedrigsten, tatsächlich auftretenden Frequenz überein.
Das Problem ist jedoch, dass sich durch Hinzufügen der Dämpfung an den Stellen SE, PEE und SEE
diese Frequenzen verschieben und mittels eines Leistungsdichtespektrums nicht mehr ermittelt werden
können. Diese sollte jedoch möglichst exakt ermittelt werden, um daraus die optimale Aktivierungsdauer
und Frequenz für das Hüpfen ableiten zu können. Dazu ist eine genaue strukturdynamische
Untersuchung nötig, wie im folgenden Kapitel gezeigt wird.
</imgcaption>
Der Wert <latex>f_{y2,approx}</latex> stimmt fast mit der niedrigsten, tatsächlich auftretenden Frequenz überein.
Das Problem ist jedoch, dass sich durch Hinzufügen der Dämpfung an den Stellen SE, PEE und SEE
diese Frequenzen verschieben und mittels eines Leistungsdichtespektrums nicht mehr ermittelt werden
können. Diese sollte jedoch möglichst exakt ermittelt werden, um daraus die optimale Aktivierungsdauer
und Frequenz für das Hüpfen ableiten zu können. Dazu ist eine genaue strukturdynamische
Untersuchung nötig, wie im folgenden Kapitel gezeigt wird.


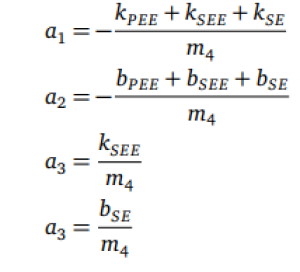



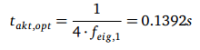
 </imgcaption>
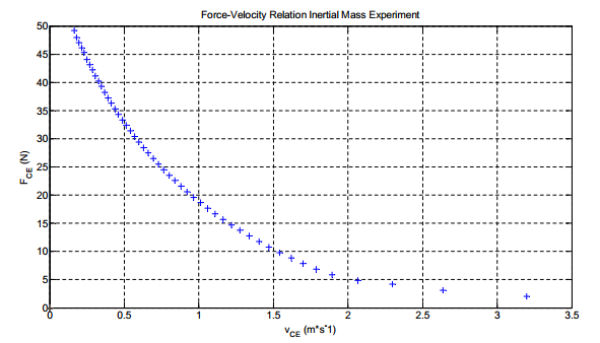
<imgcaption image14 |Kraft-Geschwindigkeits-Verhältnis des CE aus QRF, verwendete Parameter siehe Tabelle
A.4>
</imgcaption>
<imgcaption image14 |Kraft-Geschwindigkeits-Verhältnis des CE aus QRF, verwendete Parameter siehe Tabelle
A.4>
 </imgcaption>
Um die Annahme auf Korrektheit zu überprüen, wird die Simulation mit dieser Aktivierungsdauer
und mit um den berechneten Wert variierende Dauern ausgeführt und die Sprunghöhen
verglichen. Als Periodendauer wird immer das vierfache der jeweiligen Aktivierungsdauer verwendet.
Diese Versuche werden einmal ohne eine Verzögerung der Kraft <latex>F_{AE}</latex> und einmal mit einer Verzögerungzeit von <latex>t_{verzoeg} = 30ms</latex> ausgeführt. Als Sprunghöhe wird der Wert genommen, der
sich nach längerem Hüpfen einstellt. Die Ergebnisse dieser beiden Versuchsreihen sind in den
Abbildungen 7 und 8 zu sehen. Wie angenommen werden die größten Sprunghöhen mit
dem berechneten Wert (41) erreicht. Der Verlauf der Koordinaten bei periodischer Aktivierung mit
<latex>t_{akt} = \frac{1.7962}{4}</latex> und <latex>t_{verzoeg} = 30ms</latex> ist in Abbildung 9
<imgcaption image15 |Sprunghöhe in Abhängigkeit der Aktivierungsdauer t act , t verzoeg = 0, restliche Parameter
siehe A.4>
</imgcaption>
Um die Annahme auf Korrektheit zu überprüen, wird die Simulation mit dieser Aktivierungsdauer
und mit um den berechneten Wert variierende Dauern ausgeführt und die Sprunghöhen
verglichen. Als Periodendauer wird immer das vierfache der jeweiligen Aktivierungsdauer verwendet.
Diese Versuche werden einmal ohne eine Verzögerung der Kraft <latex>F_{AE}</latex> und einmal mit einer Verzögerungzeit von <latex>t_{verzoeg} = 30ms</latex> ausgeführt. Als Sprunghöhe wird der Wert genommen, der
sich nach längerem Hüpfen einstellt. Die Ergebnisse dieser beiden Versuchsreihen sind in den
Abbildungen 7 und 8 zu sehen. Wie angenommen werden die größten Sprunghöhen mit
dem berechneten Wert (41) erreicht. Der Verlauf der Koordinaten bei periodischer Aktivierung mit
<latex>t_{akt} = \frac{1.7962}{4}</latex> und <latex>t_{verzoeg} = 30ms</latex> ist in Abbildung 9
<imgcaption image15 |Sprunghöhe in Abhängigkeit der Aktivierungsdauer t act , t verzoeg = 0, restliche Parameter
siehe A.4>
 </imgcaption>
<imgcaption image16 |Sprunghöhe in Abhängigkeit der Aktivierungsdauer t act , t verzoeg = 30, restliche Parameter
siehe A.4>
</imgcaption>
<imgcaption image16 |Sprunghöhe in Abhängigkeit der Aktivierungsdauer t act , t verzoeg = 30, restliche Parameter
siehe A.4>
 </imgcaption>
<imgcaption image17 |Dynamisches Verhalten Hopper-Modell. Verwendete Parameter siehe Tabelle A.3>
</imgcaption>
<imgcaption image17 |Dynamisches Verhalten Hopper-Modell. Verwendete Parameter siehe Tabelle A.3>
 </imgcaption>
</imgcaption>