Inhaltsverzeichnis
DYN5 Mehrkörpersysteme
| Modul | DYN5 Mehrkörpersysteme |
|---|---|
| Kategorie | Dynamik |
| Autor | Cengic, Dahms |
| Voraussetzung | – |
| Bearbeitungsdauer | ca. 30 Minuten |
Lernziele
| Lehrveranstaltung | Lernziele |
|---|---|
| PS Biomechanik | - Eine Vorstellung versch. Körper entwickeln - Funktionsweise einer offenen/geschlossenen Kette nachvollziehen - Einfluss der Freiheitsgrade auf Körper und „Ketten“ |
| PS Forschungsmethoden 2 | - Den Körperschwerpunkt kennenlernen und seine Bedeutung verstehen |
Einleitung
Die Einleitung dieses Moduls beschäftigt sich mit dem starren Körper. Im Anschluss daran wird der Körperschwerpunkt (im Folgenden: KSP) behandelt. Im weiteren Verlauf werden Systeme zusammengesetzter Körper (Mehrkörpersysteme) sowie die Schwerpunktsätze erklärt. Da bei der Berechnung des KSP mathematische Formeln angewendet werden, wurde ein Tutorial hinzugefügt.
Einführendes Beispiel
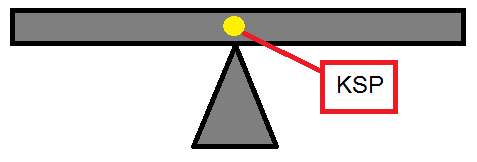
Das längliche Rechteck (s. Abbildung 1) sei ein starrer Körper. Diese besitzen eine räumliche Ausdehnung und können im Gegensatz zu Punktmassen rotieren. Dementsprechend besitzt ein starrer Körper sechs Freiheitsgrade (drei rotatorische und drei translatorische).
Auffälig in diesem Beispiel ist, dass das längliche Rechteck nicht kippt. Das Dreieck greift am Massenmittelpunkt (KSP) an und der Körper erhält sein Gleichgewicht. Die Teilmassen (links und rechts vom KSP) sind gleich und heben sich somit gegenseitig auf.
Was ist ein starrer Körper?
Ein starrer Körper ist ein Körper, dessen Körperpunkte sich alle in einem festen (starren) Abstand zueinander befinden. Durch Vergleich mit einer Punktmasse fallen weitere Eigenschaften auf: die Punktmasse vereint ihre komplette Masse in einem Punkt und besitzt keine räumliche Ausdehnung, also kein Volumen. Der starre Körper hingegen besitzt neben seiner Masse auch ein Volumen und eine Dichte. Die Punktmasse besitzt nur 3 translatorische Freiheitsgrade, der starre Körper besitzt, auf Grund seiner räumlichen Ausdehnung, neben den 3 translatorischen zusätzlich 3 rotatorische Freiheitsgrade. Der menschliche Körper besitzt auch 3 translatorische und 3 rotatorische Freiheitsgrade (aber Achtung, er ist kein starrer Körper!).
Exkurs: Freiheitsgrade
Die Freiheitsgrade definieren in welche Richtung ein Körper bewegt werden kann. Dabei wird jede individuelle Bewegungsrichtung einzeln gewertet und aufsummiert. Grundsätzlich gibt es zwei verschiedene Arten von Freiheitsgraden:
- Translatorische Freiheitsgrade geben an, ob es möglich ist den Körper im Raum zu bewegen, z. B. nach oben/unten, links/rechts oder vorne/hinten.
- Rotatorische Freiheitsgrade geben an, ob es möglich ist den Körper um verschiedene Achsen zu rotieren. Diese Achsen sind (bezogen auf den Menschen): Körperbreitenachse (z. B. Salto), Körperlängsachse (z. B. Pirouette) sowie die Körpertiefenachse (z. B. Rad schlagen).
Körperschwerpunkt
Der Körperschwerpunkt beschreibt den Massenmittelpunkt des menschlichen Körpers. Dabei handelt es sich um einen gedachten Punkt, an dem die Gravitationskraft angreift. Allerdings kann die Position des KSP variieren, denn diese ist abhängig von der Körperhaltung, sowie der Masseverteilung im Körper.
Der Mensch ist ein komplexes System, welches sich aus mehreren Körpersegmenten zusammensetzt. Diese werden in folgender Tabelle zusammen mit ihren Anteil an der Gesamtmasse aufgeführt (vgl. Seyfarth, 2005, S. 62).
| Segment | Anteil an der Gesamtmasse (%) |
|---|---|
| Kopf | 7 |
| Rumpf | 43 |
| Oberschenkel (1x) | 12 |
| Unterschenkel (1x) | 5 |
| Fuß (1x) | 2 |
| Oberarm (1x) | 3 |
| Unterarm (1x) | 2 |
| Hand (1x) | 1 |
Der Tabelle ist zu entnehmen, dass der Rumpf als alleiniges Körpersegment fast die Hälfte (43 %) unserer Gesamtmasse ausmacht, während die Hände sich mit nur 2 % minimal auf die Lage des menschlichen Massenmittelpunktes (KSP) auswirken. Die Bestimmung des KSP ist häufig in biomechanischen Analysen unabdingbar, daher wird an einem Beispiel dargestellt, wie sich dieser rechnerisch bestimmen lässt und welche Relevanz somit die Tabelle hat.
Hier nochmal die Formel zur Berechnung des KSP außerhalb des Videos:
$$\vec{S} = \frac{1}{M} \sum{m_{i}*r_{i}}$$
Massenmittelpunkt vs. geometrischer Schwerpunkt
In dem einführenden Beispiel sind die Teilmassen (jeweils links/ rechts vom KSP) gleich schwer. Dieser Körper wird als homogen bezeichnet. Zerlegt man das längliche Rechteck also in 8 gleich große Teile, so würde jedes dieser Teile dieselbe Masse aufweisen (→ die Dichte der Teilmassen ist gleich).
Wo liegt aber der Massenmittelpunkt und der geometrische Schwerpunkt bei einem inhomogenen Körper?
Anders gefragt: Wie verändern sich die Schwerpunkte, wenn die Teilmassen (links/ rechts vom KSP des Rechtecks) unterschiedlich sind?
Nehmen wir an die linke Seite wiegt zwei Kilogramm und die rechte Seite nur ein Kilogramm. Demnach müsste sich der Massenmittelpunkt nach links verschieben, d.h. das Dreieck im obigen Beispiel müsste also nach links wandern, damit das Gleichgewicht erhalten bleibt. Der geometrische Schwerpunkt allerdings ändert sich nicht, denn wie der Name verrät, beschäftigt sich dieser mit der Geometrie des Körpers und nicht mit der Massenverteilung.
Mehrkörpersysteme
Die vorigen Abschnitte haben sich mit den Segmenten des menschlichen Körpers beschäftigt. Ein Mehrkörpersystem meint nun ein System von Einzelkörpern (in diesem Fall Körpersegmente) welche durch Gelenke gekoppelt sind. Ein Beispiel dafür ist der menschliche Körper.
Für die Biomechanik stellt dies ein wichtiges Forschungsgebiet dar. Mit den gewonnenen Erkenntnissen lassen sich beispielsweise Bewegungen optimieren oder individuell angepasste Prothesen entwickeln.
Bei der weiteren Auseinandersetzung mit den Mehrkörpersystemen spielen die Begrifflichkeiten geschlossene und offene kinematische Kette eine wesentliche Rolle (vgl. Abbildung 2). Von einer kinematischen Kette spricht man, wenn es sich um eine Verbindung von mehreren starren Körpern handelt, die mit Gelenken miteinander verbunden sind. Offen ist die Kette dabei, wenn der letzte Körperteil frei im Raum beweglich ist, geschlossen, wenn die Verbindung der Einzelkörper einen geschlossenen Kreis ergibt. Dabei kann der Kreis (wie in Abb. 2) auch mithilfe des Bodens geschlossen werden.
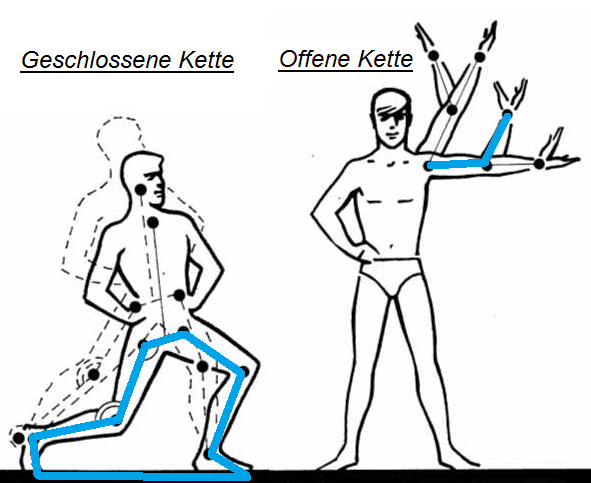
Eine interessante Frage ist die mathematische Ermittlung der Anzahl von Freiheitsgraden innerhalb einer offenen/geschlossenen kinematischen Kette. Bei den offenen kinematischen Ketten entspricht diese exakt der Anzahl der Segmente. Im obigen Beispiel (s. Abb. rechts) hat diese zwei Segmente und somit zwei Freiheitsgrade.
Aber wie lautet die Formel für geschlossene kinematische Ketten?
Die Anzahl lässt sich mittels folgender Gleichung bestimmen: $F = g - 3$.
Die Variable $F$ entspricht dabei der Anzahl der Freiheitsgrade und $g$ die Zahl der Segmente. Beispielsweise hat ein Körper mit fünf Segmenten innerhalb einer geschlossenen kinematischen Kette zwei Freiheitsgrade.
Schwerpunktsätze
Abschließend werden noch die zwei Schwerpunktsätze vorgestellt, die aber zunächst eine Betrachtung des Unterschieds zwischen äußeren und inneren Kräften voraussetzt. (vgl. Seyfarth, 2005, S. 72).
Innere Kräfte beschreiben Kräfte, die zwischen den Körpersegmenten wirken, z.B. Muskelkräfte oder Gelenkkräfte. Äußere Kräfte hingegen treten bei der Wechselwirkung Umwelt-Bewegungsapparat (hier: der Mensch) auf. Gemeint sind damit bspw. entstandene Kräfte zwischen Hand und Sportgerät oder Bodenreaktionskräfte. Diese Kräfte wirken von außen auf ein mechanisches System ein.
Am Beispiel des Basketballs verdeutlicht:
- Innere Kraft: Druckluft, Material, etc.
- Äußere Kraft: Gewichtskraft (der Körper wird von der Erde angezogen), Luftwiderstand, etc.
Schwerpunktsatz I:
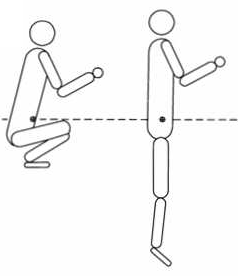
Der erste Satz besagt, dass in einem abgeschlossenen System (keine äußeren Kräfte) die Lage (bzw. die Bewegung) des KSP im Raum nicht verändert werden kann. Folgende Grafik veranschaulicht, dass selbst das Anhocken der Beine die Position (bzw. die Bewegung) des KSP nicht ändert. Das gilt z.B. für die Bahn des KSP bei einem vertikalen Sprung. Egal wie man seine Körperteile während des Sprunges zueinander ausrichtet, man wird in jedem Fall einfach nur hoch springen und wieder runterfallen.
Schwerpunktsatz II:
Dieser Satz beschäftigt sich mit dem nicht abgeschlossenem System (es wirken äußere Kräfte). Er besagt einfach nur, dass alle Kräfte am Systemschwerpunkt (KSP) angreifen, z.B. die Bodenreaktionskraft (FB) oder die Gewichtskraft (FG).

Zusammenfassung
Mit Hilfe der Bestimmung von KSP und Freiheitsgraden (engl. Degrees of Freedom) lassen sich zahlreiche Bewegungen aus dem Sport biomechanisch beschreiben und analysieren. Aus diesen Betrachtungen heraus, ergeben sich Optimierungsmöglichkeiten im Bewegungsablauf. Durch weitere Betrachtungen, wie zum Beispiel mithilfe der Schwerpunktsätze, lassen sich weitere Abschätzungen bei sportlichen Bewegungen im Bezug auf Ursache und Wirkungsbeziehung tätigen.
Kontrollfragen
<spoiler |1. Ist der menschliche Körper ein starrer Körper? Falls nein, worin liegen die Unterschiede?> Der menschliche Körper ist kein starrer Körper, vielmehr ist er ein Mehrkörpersystem bestehend aus vielen Körperteilen. Die Definition des starren Körpers besagt, dass dieser aus vielen Punktmassen besteht, die ihm festen Abstand zueinander angeordnet sind. Auf Grund unserer Gelenke, ist das beim menschlichen Körper nicht der Fall. Was unser Körper allerdings mit einem starren gemein hat, sind die Freiheitsgrade. Wir besitzen 6 Stück, drei rotatorische und drei translatorische. </spoiler>
<spoiler |2. Wie berechnet sich der KSP und wie lässt sich dieser beeinflussen?> Der KSP wird von der Körperhaltung und der Masseverteilung (also Dichteverteilung) im Körper beeinflusst. Der KSP lässt sich berechnen, indem man die Produkte der Massepunkte und ihrer Abstände zum Ursprung addiert und durch die Gesamtmasse teilt. Mit Ursprung ist der Punkt (0 | 0) des Koordinatensystems gemeint, welches man 'über' den zu betrachtenden Körper legt. Als Ergebnis der Formel für den KSP erhält man den Ortspunkt (mit x - und y - Koordinate) des KSP. </spoiler>
<spoiler |3. Wie viele Freiheitsgrade hat eine offene/geschlossene Kette bestehend aus 2 (3, 10) Segmenten?>
Generell haben offene Ketten soviele Freiheitsgrade wie sie Segmente besitzen. Um die Freiheitsgrade einer geschlossenen Kette auszurechnen, gibt es folgende Formel: Freiheitsgrade = Segmente - 3.
Eine offene Kette mit 2 Segmenten hat 2 Freiheitsgrade.
Eine offene Kette mit 3 Segmenten hat 3 Freiheitsgrade.
Eine offene Kette mit 10 Segmenten hat 10 Freiheitsgrade.
Eine geschlossene Kette mit 2 Segmenten hat <0 Freiheitsgrade.
Eine geschlossene Kette mit 3 Segmenten hat 0 Freiheitsgrade.
Eine geschlossene Kette mit 10 Segmenten hat 7 Freiheitsgrade.
</spoiler>
Literatur
Seyfarth, A. (2005). Einführung in die Biomechanik. Teil C: Dynamik der Rotation. Präsentationsfolien im Rahmen der Veranstaltung Einführung in die Biomechanik WS 2005/06. Jena: Institut für Sportwissenschaften.