Inhaltsverzeichnis
DYN6 Reibung
| Modul | DYN6 Reibung |
|---|---|
| Kategorie | Dynamik |
| Autor | Gossmann, Cengic, Dahms |
| Voraussetzung | DYN01-DYN04 |
| Bearbeitungsdauer | ca. 60 Minuten |
Lernziele
| Lehrveranstaltung | Lernziele |
|---|---|
| PS Biomechanik | - Verschieden Reibungsarten kennenlernen - Wo/wann treten diese auf? - Welchen Einfluss haben sie? |
Einleitung
In diesem Modul werden verschiedene Arten der Reibung behandelt. Themen sind zum einen die äußere Reibung, hierbei handelt es sich um die von außen einwirkenden Kräfte an bewegten Objekten am Boden, in der Luft und im Wasser. Im Fokus stehen Haft- und Gleitreibung sowie die Rollreibung. Zum anderen wird die innere Reibung, auch als Viskosität bezeichnet, erläutert.
Im zweiten Teil dieses Moduls werden drei wesentliche Widerstände vorgestellt, die ein sich bewegender Körper aufgrund seiner Form und des Mediums, in dem er sich befindet, erzeugt. Es wird der Wellenwiderstand, der Reibungswiderstand und der Formwiderstand erklärt.
Diese Widerstandskräfte, innere und äußere, wirken im Sport z. B. bei Sportgeräten, mit denen sich Sportler fortbewegen (Schlittschuh, Bob, Fahrrad) oder auch bei Sportgeräten, die wir bewegen (Diskus, Speer).
Äußere Reibung
Als äußere Reibung wird der Kontakt zwischen zwei Festkörpern beschrieben und in Haft- und Gleitreibung unterschieden. Versucht man einen ruhenden Körper auf einer Oberfläche zu bewegen, so haftet er zunächst, bis eine gewisse Kraft überschritten wird.
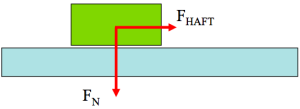
„Physikalisch betrachtet sind es hemmende Kräfte, die der Bewegung entgegengesetzt sind und stets parallel zur Berührungsfläche wirken“ (Wick, 2009, S. 42). Die Reibungskraft ist dabei proportional abhängig von der Normalkraft $F_N$, die immer senkrecht auf der Berührungsfläche steht. Weitere Einflussfaktoren spiegelt der Haftreibungskoeffizient ($\mu$) wieder, denn „… er hängt von den Materialien, aus denen die einander berührenden Oberflächen bestehen, sowie von deren Temperaturen ab“ (Tipler & Mosca, 2009, S. 137). Dabei kann es sich zum Beispiel um Gummi auf Asphalt oder Holz auf Holz handeln. Eine Skizze soll diesen Sachverhalt verdeutlichen:
Die Reibungskraft (hier angegeben mit $F_{HAFT}$ ) und die Normalkraft ($F_N$) stehen in einem proportionalen Verhältnis, welches sich anhand der Formel zur Bestimmung der Reibungskraft zeigen lässt.
;#; $F_{HAFT} = \mu * F_N$ ;#;
Der Reibungskoeffizient ($\mu$) ist dimensionslos (ohne Einheit) und gibt das Verhältnis zwischen Reibungskraft und Normalkraft an.
Die Frage die sich nun stellt ist, wie sich die Haftreibung von Gleitreibung unterscheidet?
Haft- und Gleitreibung
Der Unterschied zwischen Haft- und Gleitreibung besteht darin, dass die Gleitreibung auftritt, wenn sich zwei Kontaktflächen relativ zueinander bewegen, während bei der Haftreibung die Kontaktflächen in der Position verharren. Die Gleitreibungskraft ist meist etwas geringer als die Haftreibungskraft. Dieser Sachverhalt soll an einem Beispiel verdeutlicht werden:
Wollen wir eine Holzkiste in eine bestimmte Richtung bewegen, so müssen wir eine gewisse Kraft (größer als das Maximum der Haftreibungskraft) aufwenden, bis sich die Kiste in Bewegung setzt. In dem Moment, in der die Bewegung eingeleitet wurde, ist der Kraftaufwand geringer, da sich die Haftreibungskraft verändert hat. Daher fällt es jetzt leichter die Kiste voranzuschieben. Die Ursache liegt daran, dass der Gleitreibungskoeffizient kleiner ist als der Haftreibungskoeffizient.
Rollreibung
Beim Fahren mit dem Auto auf der Straße erfährt ein Reifen stets eine Kraft die zur Abnutzung führt. „In der Realität übt die Straße daher auf den Reifen eine Rollreibungskraft $F_{RR}$ aus, die der Bewegung entgegenwirkt“ (Tipler & Mosca, 2009, S. 138). Wie zuvor beschrieben wirkt diese Kraft entgegen der Fahrtrichtung, daher stellt sich die Frage wie man die Geschwindigkeit trotz der Reibung halten kann?
Es muss neben der Antriebskraft eine zusätzliche Kraft auf das Rad wirken damit die Geschwindigkeit beibehalten werden kann. Dabei ist es entscheidend, dass der Betrag der Kraft (in Fahrtrichtung), gleich dem Betrag der Rollreibungskraft (Kraft von der Straße auf das Rad) beträgt. Dieser Zusammenhang verdeutlicht sich in der letztendlichen Gleichung zur Rollreibung:
;#; $|F_{RR}| = \mu_{RR} * |F_N|$ ;#;
Der Rollreibungskoeffizient $\mu_{RR}$ gibt dabei das Verhältnis zwischen der Rollreibungs- und Normalkraft für die betrachteten Kontaktflächen an. Eine Eisenbahn zum Beispiel hat einen geringeren Rollwiderstand (0,002) im Vergleich zu einem Reifen auf Asphalt (0,02). Das bedeutet das eine Eisenbahn weniger Kraft benötigt um die Geschwindigkeit beizubehalten.
Widerstände
Auch wenn er nicht immer wahrgenommen wird, spielt der Widerstand bei all unseren Bewegungen eine große Rolle. Weil Bewegungen stets in einem Medium (Wasser, Luft) stattfinden, werden ständig Widerstände erzeugt. In diesem Abschnitt werden drei wesentliche Widerstände vorgestellt: der Wellenwiderstand, der nur im Wasser auftritt, sowie der Reibungs- und der Formwiderstand, welche bei Bewegungen sowohl im Wasser als auch in der Luft stets präsent sind.
Wellenwiderstand
Der Wellenwiderstand tritt im Wasser auf, wenn durch einen Schwimmer Wasser verdrängt wird. Das Wasser weicht zunächst zur Oberfläche hin aus. Vor dem Schwimmer entsteht also ein Wellenberg. Physikalisch betrachtet entsteht durch die Arbeit des Schwimmers potentielle Energie. Im Wechselspiel aus potentieller und kinetischer Energie pflanzt sich die Welle fort. Für den Schwimmer bedeutet das, dass er aus dem Wellental, welches durch die Ausbreitung der Welle vor ihm entstanden ist, jedes Mal wieder nach oben herausschwimmen muss. Der geringste Wellenwiderstand tritt übrigens bei einer Tauchtiefe auf, die der 3-fachen des Körperdurchmessers entspricht, also bei etwa 70 - 90cm (vgl. Blickhan et al., 2005, S. 14; Skript GK Schwimmen, S. 6).
Reibungswiderstand
Fließt ein Medium (Flüssigkeit oder Gas bzw. Wasser oder Luft) an einem Körper vorbei, so bleibt es, wegen Adhäsion (auch Anhangskraft genannt), an der Oberfläche des Körpers haften. Um den Körper bilden sich Strömungsschichten (Abb.1). Die Geschwindigkeit der ersten anliegenden Schicht (grün) ist nahezu identisch mit der des Körpers. Die Geschwindigkeit der äußeren Schichten nimmt mit steigendem Abstand ab. Grund dafür ist die Reibung zwischen den Schichten. Die Strömung zwischen den Schichten ist entweder turbulent (Schichten verwirbeln) und hat damit auch eine sehr hohe Reibung oder laminar (Schichten gleiten 'glatt' nebeneinander), wodurch die Reibung eher gering ist (vgl. Hahn & Strass, 2009, S. 371f)
Eine Erklärung zu laminaren und turbulenten Strömungen gibt es unter Exkurs: Strömungen im nächsten Modul.
Bei einem Schwimmer z.B. haftet die Strömungsschicht, die dem Körper am nächsten ist, wegen möglicher Behaarung oder Badebekleidung an ihm. Durch die Reibung zwischen den anderen Schichten, kommt es dann zu einem Reibungswiderstand.
<imgcaption image2 |Laminare Strömungsschichten um Körper (Quelle:Wikipedia 'Laminare Strömung')>
 </imgcaption> <imgcaption image3 |Sogwirkung durch Verwirbelung (Quelle: https://www.univie.ac.at/physikwiki/images/2/24/Wirbelbildung2.svg)>
</imgcaption> <imgcaption image3 |Sogwirkung durch Verwirbelung (Quelle: https://www.univie.ac.at/physikwiki/images/2/24/Wirbelbildung2.svg)> </imgcaption>
</imgcaption>
Wie oben erwähnt, haben die Strömungsschichten unterschiedliche Geschwindigkeiten, wenn sie am Körper entlanggleiten. Treffen sie nach Umströmen des Körpers wieder aufeinander, führt dies zu einer Wirbelbildung hinter dem Körper, wodurch eine Sogwirkung ensteht (Abb.2). Zusätzlich zum Reibungswiderstand muss diese Sogkraft vom Schwimmer überwunden werden.
Die Formel, mit der sich der Reibungswiderstand abschätzen lässt lautet:
;#; $F = \eta \frac{\Delta{ v}}{\rho}A$ ;#;
Erklärung:
$\eta$ = die Viskosität (Zähigkeit) des Mediums
$\Delta{ v}$ = Differenz in der Geschwindigkeit der Wasserschichten
$\rho$ = Dichte des Mediums
$A$ = Fläche der mit Wasser bedeckten Oberfläche (Wenn das Fluid Wasser ist)
Formwiderstand
Wie der Name schon sagt, beschreibt der Formwiderstand den Widerstand, der durch die Form des Körpers bei Bewegung in der Luft oder in Wasser erzeugt wird. Es ist aber nicht nur die Form, es spielen auch weitere Parameter eine Rolle. Daher zuerst die Formel, mit dem der Formwiderstand berechnet werden kann:
;#; $F = A * c_W * \frac{\rho}{2} * v^2$ ;#;
$A$ ist die projizierte Fläche des Körpers senkrecht zur Anströmungsrichtung. $v$ ist die Geschwindigkeit, mit der sich der Körper bewegt. $\rho$ ist die Dichte des Wassers/Luft. $c_W$ ist der Widerstandsbeiwert. Der Wert ist dimensionslos und drückt aus, wie gut die Form die Strömung an sich vorbei lässt. Je höher der Wert, desto schlechter gelangt die Strömung am Körper vorbei und desto größer ist auch der Formwiderstand (vgl. Strass & Hahn, 2009, S. 372f).
Tutorial: Reibung
Dieses Tutorial gibt einen vertiefenden Einblick in die drei Reibungsarten: Haft-, Gleit- und Rollreibung.
Anmerkung: Eine Rivision dieses Videos läuft gerade. Die angeführten Kapitelbez. stimmen daher nicht mit den Aktuellen überein.
Zusammenfassung
In diesem Wiki Modul wurden die einzelnen Komponenten der äußeren und inneren Reibung erläutert. Die Sortierung dieser Reibungskräfte der Größe nach, soll nochmals das Verständnis stärken:
;#; $Rollreibung < Gleitreibung < Haftreibung$ ;#;
Außerdem wurde die Viskosität (Maß für innere Reibung) erklärt. Da sich aus Reibung Widerstände ergeben, wurden der Wellen-, Reibungs- und Formwiderstand kurz erläutert.
Kontrollfragen
<spoiler |1. Was unterscheidet Haft- und Gleitreibung? Wann rutscht man? Antwort> Haftreibung ist die Reibung, die besteht wenn ein Gegenstand an einem anderen, oder auf dem Boden haftet. Gleitreibung ist die Reibung, die besteht, wenn ein Gegenstand gleitet. Man rutscht, wenn die Haftreibung überwunden wird. Die Haftreibung ist größer als die Gleitreibung. Das liegt daran, dass der Haftreibungskoeffizient größer ist, als der Gleitreibungskoeffizient. </spoiler>
<spoiler |2. Welche Rückschlüsse für einen Schwimmer lassen sich aus den Parametern für den Formwiderstand gewinnen? In welchen anderen Sportarten bringt eine Reduktion des Formwiderstandes eine Verbesserung? Antwort>
Der einzige Parameter des Formwiderstandes, den der Schwimmer ändern kann, ist die Fläche senkrecht zur Anströmungsrichtung. Will der Schwimmer den Formwiderstand also verkleinern, (kann er natürlich seine Geschwindigkeit verringern, aber er möchte ja wahrscheinlich möglicht schnell sein) sollte er sich möglichst 'flach' im Wasser befinden, sodass sein Körper möglichst parallel zur Strömung ist. So erzeugt er eine möglichst kleine Fläche senkrecht zur Anströmung.
Diese Fläche spielt außerdem z.B. beim Skifahren eine Rolle: wenn man Schuss fahren will, sollte man sich ducken, so erzeugt man durch seinen Körper möglichst wenig Formwiderstand.
Auch beim Turmspringen spielt der Formwiderstand eine Rolle. Wenn der Springer eintaucht, versucht er die Fläche, mit der er auf das Wasser auftrifft, möglichst klein zu halten und taucht daher mit dem Kopf (bzw. mit den Händen) zuerst ein.
</spoiler>
<spoiler |3. Bei einem Auto werden zwei neue Räder montiert, da ein Reifen defekt war. Wo sollten die neuen Räder montiert werden: vorn oder hinten? Antwort>
Die Räder sollten hinten montiert werden, um so bei nasser Fahrt ein Ausscheeren zu vermeiden.
Eine Erklärung auf Englisch findet Ihr unter dem folgenden Link oder im folgenden Video:
http://blog.allstate.com/new-tires-rear/?cid=CSY-PB-BLOG&att=OB_New-Tires-To-The-Rear
</spoiler>
Literatur
Blickhan, R., Seyfarth, A. & Wank, V. (2005). Einführung in die Biomechanik, Teil D: Äußere Kräfte, Muskel. Unveröffentlichtes Manuskript. Jena: FSU Jena.
DocCheck Flexikon. Das Medizinlexikon zum Medmachen. Zugriff am 13.11.2013 unter http://flexikon.doccheck.com/de/Viskosit%C3%A4t
Formel-Sammlung.de. Die Quelle für Fomeln, Tabellen und Lösungen. Zugriff am 23.10.2013 unter http://www.formel-sammlung.de/formel-Reibungszahlen-3-25-150.html
Hahn, A. & Strass, D. (2009). Biomechanik des Schwimmens. In Gollhofer, A. & Müller, E. (Hrsg), Handbuch Sportbiomechanik (S. 364 - 389). Schorndorf: Hofmann-Verlag.
Skript GK Schwimmen, Unveröffentlich (2010). Darmstadt: TU Darmstadt.
Tipler, P. A. & Mosca, G. (2009). Physik - für Wissenschaftler und Ingenieure. 6. deutsche Auflage. Heidelberg: Spektrum Adademischer Verlag.