Inhaltsverzeichnis
WP1503 SimMechanics
| WP1503 SimMechanics | |
| Veranstaltung | PS Biomechanik |
| Autor | Patrick Burghardt, Holger Dieterich, Andreas Döring |
| Bearbeitungsdauer | ca. 60 min (davon ca. 30 min Tutorial) |
| Vsl. Fertigstellung | 24.06.2015 |
| Seite in Bearbeitung |
(Sämtliche in diesem Wiki verwendeten Abbildungen sind selbsterstellte Screenshots)
Einführung
Das Wiki ist eine Einführung in das Simulationsprogramm SimMechanics, welches zur Modellierung von Mehrköpersystemen dient. Zunächst folgt eine kurze Motivation zum Wiki, welche u.a. den Bezug zur Biomechanik herstellen soll, gefolgt von einer kurzen Vorstellung des Programms SimMechanics. Der Hauptteil des Wikis jedoch befasst sich mit einem tutoriellen Einstieg in das Programm selbst. Durch das Tutorial soll dem Leser/ der Leserin ein Einblick in die grundlegende Steuerung des Programms gegeben werden und ein grobes Verständnis für die einzelnen Funktionen und Möglichkeiten eröffnet werden. Für die Abarbeitung des Tutorials sind Kenntnisse in MATLAB und Simulink von Vorteil. Ziel des Tutorials soll eine erste, sehr simple Simulation einer Klimmzugbewegung sein. Abgeschlossen wird das Wiki mit einem Ausblick, welcher dem Leser/ der Leserin die vielschichtigen Möglichkeiten aufzeigen soll, die das Programm noch offen hält.
Diese Wiki soll einen vereinfachten Einblick in die Materie des Programms liefern. Definitionen und Erläuterungen sind abgespeckt und gleichzeitig auf das Tutorial angepasst formuliert worden. Zu Vertiefung oder bei Interesse empfiehlt es sich dem im Literaturverzeichnis aufgeführten Link zum Mathlab-Manual zu folgen.
verfasst von Patrick Burghardt
Motivation
Der vorherige Clip, zeigt eine von vielen Varianten, eine Klimmzugbewegung durchzuführen. Doch bei welcher Bewegung wirken welche Kräfte? Welche Ausführung ist trainingstechnisch wertvoller? Wie kann der komplexe Bewegungsvorgang möglichst einfach aber genau beschrieben werden?
Diese Fragen können oft nur unzureichend oder mit hohem Aufwand durch reine Messungen an einem Probanden beantwortet werden. In diesen Fällen ist es sinnvoll das reale System mit Hilfe eines Modells simulieren zu können. Für das Feld der Biomechanik sind die Vorteile einer Simulation das Ausbleiben von Erschöpfung, die bessere Wiederholungsgenauigkeit und die damit verbundene Vergleichbarkeit, ebenso die Vermeidung von gesundheitlichen Schäden bei riskanteren Bewegungsabläufen. Des weiteren ist es möglich eine Simulation zu jedem Zeitpunkt der Bewegung anzuhalten. Visualisierungstools ermöglichen gleichzeitig eine Darstellung von mechanischen Vorgängen und Zustandsgrößen. Die genauen Größen der wirkenden Kräfte auf jeden Muskel bzw. auf jedes Gelenk kann durch die Simulation errechnet werden, ebenso auch weitere Größen wie Drehmomente oder Wirkungspunkte, Trägheiten, usw. Dennoch kann auf Messungen mit Probanden nicht verzichtet werden. Sind Größen der wirkenden Kräfte auf jeden Muskel und auf jedes Gelenk bekannt, so kann mit Hilfe der Messungen das Modell bewertet werden.
Durch das Benutzen einer Simulationssoftware in der Biomechanik wird es ermöglicht, umgekehrt zum Normalfall, eine Brücke von der Theorie zur Praxis zu schlagen. Die Modellhafte Nachbildung kann Aufschluss über Bewegungsabläufe im Sport oder Training liefern und zugleich für die Biomechanik Daten liefern, welche aus einer „realen“ Messung nicht hätten erschlossen werden können.
Bleibt die Frage, wieso wir uns in diesem Wiki für das Programm SimMechanics entschieden haben. SimMechanics selbst ist ein Unterprogramm des in der Forschung und Technik weit verbreiteten Programms MATLAB. Eine Einführung in MATLAB wird in MATLAB WIKI gegeben. MATLAB ist in Universitäten und Firmen, vor allem aber im Forschungs- und Entwicklungsbereich weit verbreitet. SimMechanics, als Mehrkörpersimulationsprogramm, ermöglicht einfach ausgedrückt, die physikalische Modellierung von realen Bewegungen hinein in eine simulierte Bewegung. Die Arbeit innerhalb des Programms findet ausschließlich mit physikalischen Größen statt, aus welchen die Bewegungen heraus definiert und modelliert werden. Der große Vorteil den man an dieser Stelle genießt ist der, dass die verwendeten Modelle aus den Programmen MATLAB und Simulink direkt mit SimMechanics gekoppelt und in dieses integriert werden können. Die graphische und funktionelle Ausarbeitung des Modells wird dadurch deutlich erweitert und verfeinert, was schlussendlich auch in der Simulation zum Vorschein kommt.
Es folgt nun noch eine kurze Vorstellung des Programms und anschließend das Tutorial.
verfasst von Patrick Burghardt
SimMechanics - Was ist das?
In diesem Abschnitt wollen wir eine kurze Vorstellung des Programms vornehmen, um einen oberflächlichen Einblick über die Möglichkeiten der hier vorgestellten Software zu erhalten.
SimMechanics bietet einen Raum um das Wirken einzelner Starrkörper aufeinander zu untersuchen, was auch Mehrköper-Simulation genannt wird. Mehrkörpersysteme mit Starrkörpern werden im Wiki DYN5 Mehrkörpersysteme erklärt. Die Mehrkörper-Simulation in SimMechanics findet im drei dimensionalen Raum statt. Es lassen sich mechanische Systeme, so wie Roboter, Maschinen, Körperformen usw. virtuell konstruieren. Um ein solches Mehrkörper-System zu erschaffen, verbindet man eine Vielzahl von „Blöcken“, welche Körperteile, Gelenke und Beschränkungen darstellen. SimMechanics formuliert und löst im Hintergrund soweit selbstständig alle nötigen Bewegungsgleichungen für das gesamte mechanische System, so dass der User die Blöcke, ähnlich wie Lego-Steine nur zusammensetzen muss. Ein weiteres Feature von SimMechanics ist die Möglichkeit CAD-Modelle zu importieren. SimMechanics selbst verfügt über dies hinaus noch eine Visualisierungsfunktion, welche die Darstellung eines dynamischen Systems in einer 3D-Animation überführt.
Ein weiteres Feature von SimMechanics ist die (mögliche) Parametrisierung der konstruierten Modelle durch die Benutzung von Variablen und Befehlen, via der Mathe-Software MATLAB. Außerdem ist es möglich das Design des Regelsystems der Mehrkörper-Konstruktion via Simulink zu gestalten. Simulink ist eine Modellierungssoftware der Mathe-Software MATLAB. SimMechanics selbst ist ein Unterprogramm von Simscape, in dem die mechanische Komponenten abgebildet werden können. Simscape wiederum, als Erweiterung von Simulink, bietet weitere Unterprogramme für den Bereich z.B. der Hydraulik, Pneumatik oder Elektrik.
Zusammengefasst, bietet SimMechanics eine Vielzahl an Möglichkeiten mechanische Modelle bis hin ins kleinste Detail zu konstruieren und diese in einer Simulation zu testen. Dabei beschränkt sich die Software nicht nur auf die mechanischen und technischen Zusammenhänge, sondern ermöglicht zudem eine optische Anpassung und Optimierung. Das Programm selbst nutzt dabei vorgefertigte Gleichungen und Befehle, sodass, ähnlich einem Baukasten-Prinzip, der User (einfach formuliert) die Steine zusammensetzen kann und lediglich ihre Größe zu bestimmen hat.
verfasst von Patrick Burghardt & Holger Dieterich
Exkurs: Tutorial
In diesem Tutorial wollen wir dem Wiki-Leser einen Einblick in die Modellierung mit SimMechanics gewähren. Die Bedienung und der Nutzen dieser Software werden an einem einfachen Modell zur Simulation eines Klimmzuges verdeutlicht werden. Nach der Durcharbeitung hat der Leser das grundlegende Vorgehen verstanden und kann eigene Erweiterung hinzufügen oder das Vorgehen auf eigene Modelle übertragen.
<spoiler| Wer sich für das Tutorial interessiert, kann auf den Show-Button drücken und dieses durcharbeiten (die Inhalte des Tutorials werden nicht abgefragt)> Die SimMechanics Modell-Vorlage
Zunächst muss Matlab gestartet werden. Erste Schritte mit diesem Softwarepaket sind in den Wikis zur Modellierung beschrieben.
Im Matlab Command Window führen wir den Befehl smnew aus (Bild 1).

Dadurch öffnen sich die SimMechnics Library (Bild 2) 
und eine Simulink-Vorlage mit Basis-Blöcken für SimMechanics (Bild 3).

Alle Blöcke können durch Doppelklick geöffnet werden. Im sich öffnenden Fenster wird dann eine Beschreibung der Funktionen angezeigt. Außerdem können Parameter eingesehen und geändert werden. Die SimMechanics Oberfläche mit den einzelnen Blöcke werden im Folgenden kurz erklärt:
- Solver Configuration: Für die Zeitintegration, die zum Lösen der Bewegungs-Differentialgleichungen nötig ist, kann hier der Löser an das jeweilige Systemverhalten angegeben werden. Ein gute Erklärung befindet sich unter GM 1 Numerik
- World Frame: Ursprungskoordinaten-System. Wird ein Körper mit diesem Block verbunden, so unterbindet dies jede Bewegung des Körpers und entspricht somit im übertragenen Sinne einer Befestigung am Erdboden.
- Mechanism Configuration: Hier kann eine konstante Beschleunigung vorgeben werden. Standardmäßig ist die Erdbeschleunigung entgegen der z-Richtung eingestellt.
- Solid: Hier können Starrkörper über deren Parameter definiert werden. Form, Trägheit und Darstellung können einfach eingestellt werden.
- Rigid Transform: Koordinatentransformation zwischen Koordinatensystemen
- Simulink-PS Converter/PS-Simulink Converter: Der Converter wandelt das SimMechanics Signal (physikalische Signal) in ein Simulink Signal um und vice versa.
- Scope: Der Scope dient zur grafischen Darstellung von Signalen und wird ebenfalls in MM 2 Muskelaktivierung behandelt.
- Bidirektionale Signale in der SimMechanics-Ebene haben eine Anschluss-Bezeichnung mit F oder B. F steht für Follower und B für Base.
Hinzufügen und Anpassen von Blöcken
Zuerst sollte das automatisch erstellte Simulink-Modell aus Bild 3 gespeichert werden. Beispielsweise im Matlab-Arbeitsverzeichnis unter dem Datei-Namen model.slx.
Nun wollen wir Gelenke in das Modell einfügen. Gelenke reduzieren die Anzahl der Bewegungsfreiheitsgrade der Körper mit denen sie gekoppelt sind. In SimMechanics gibt es Rotationsgelenke und Translationsgelenke.
Durch einen Doppeltklick können in der SimMechanics-Bibliothek sm_lib die einzelnen Gruppen geöffnet werden. Nach dem Öffnen der Gruppe Joints erscheint nach dem Anklicken der verschiedenen Gelenk-Blöcke die jeweils zugehörige Beschreibung. Der Beschreibung des Revolute Joint entnehmen wir, dass sich das Drehgelenk nur um die z-Achse drehen kann. Per Drag & Drop fügen wir ein Revolute Joint in model.slx ein. Am besten positioniert man es rechts neben dem Rigid Transform-Block (Bild 4).

Als nächstes drehen wir den Rigid Transform zweimal. Eine Drehung kann entweder durch Anklicken mit der rechten Maustaste und Auswählen von Rotate & Flip → ClockWise oder durch Drücken von Strg + R ausgeführt werden. Durch die Drehung gelangt der Anschluss mit F auf die linke Seite. Diesen Anschluss verbinden wir mit der Verbindung von Solver Configuration, World Frame und Mechanism Configuration.
Ähnlich verfahren wir mit dem Revolute Joint: Den Revolute Joint-Block zweimal drehen und (Anschluss F) mit dem Rigid Transform-Block (Anschluss B) verbinden. Unser Modell sollte nun aussehen wie in Bild 5:

Wir wollen nun die Einstellungen des Rigid Transform-Blocks ändern. Der Dialog öffnet sich durch Doppeltklick auf den Block. Dort wählen wir die Einstellungen aus Bild 6:

Durch Klicken auf Apply und anschließend auf OK werden die Einstellungen gespeichert und das Fenster wieder geschlossen. Durch die getätigten Einstellungen wurde das Koordinaten-System 90° um die x-Achse gedreht. Dies ist nötig, da das Drehgelenk nur um die z-Achse rotieren kann.
In der SimMechanics Library sind noch die Gruppe der Joints geöffnet. Durch Klicken auf ![]() kann zur ursprünglichen Ansicht zurückgekehrt werden. Von dieser wechseln wir nun durch Doppeltklick in die Frames and Transforms-Gruppe.
kann zur ursprünglichen Ansicht zurückgekehrt werden. Von dieser wechseln wir nun durch Doppeltklick in die Frames and Transforms-Gruppe.
Per Drag & Drop fügen wir einen Rigid Transform-Block in das Modell ein. Eine geeignete Position ist rechts neben dem Revolute Joint-Block wie auf Bild 8.

Anschließend verbinden wir die B-Anschlüsse vom Revolute Joint und dem neuen Rigid Transform-Block. Dessen Einstellung ändern wir durch einen Doppeltklick wie in Bild 9 dargestellt. Der zweite Rigid Transform-Block stellt eine Rücktransformation dar. Diese Technik wird in SimMechanics genutzt, um einheitliche Schnittstellen zu gewährleisten.
 Durch Klicken auf Apply und OK wird der Dialog wieder geschlossen. Es ist wichtig unbedingt ein . als Dezimaltrennzeichen einzugeben, da Matlab ein , als Trennung von Werten interpretiert.
Durch Klicken auf Apply und OK wird der Dialog wieder geschlossen. Es ist wichtig unbedingt ein . als Dezimaltrennzeichen einzugeben, da Matlab ein , als Trennung von Werten interpretiert.
Arbeiten mit Sub-Systemen
Wir wollen nun ein Sub-System erzeugen. Ein Sub-System besteht aus der Zusammenfassung von mehreren Blöcken. Wir fassen die beiden Rigid Transform-Blöcke und den Revolute Joint-Block zu einem Subsystem zusammen, indem wir die linke Maustaste gedrückt halten und dabei ein Rechteck um die drei Blöcke ziehen. Hierdurch werden die Blöcke markiert. Nach einem Rechtsklick auf eines der markierten Objekte wählen wir Create Subsystem from Selection. Es wird ein Sub-System erzeugt, dessen Name standardmäßig Subsystem ist. Durch Klicken auf den Namen ändern wir diesen in Handgelenk, da dieses Subsystem später das Verhalten des Handgelenks beschreibt. Bei Bedarf kann noch die Größe des Sub-System-Symbols angepasst werden. Das Modell sollte dann so aussehen wie in Bild 10.
 In das Modell fügen wir nun noch zwei Rigid Transform-Blöcke und ein Solid-Block ein. Diese werden untereinander und mit dem Handgelenk-Sub-System verbunden wie in Bild 11 verbunden. Die Rigid Transform-Blöcke sind in der Frames and Transforms-Gruppe zu finden, der Solid-Block in der Body Elements-Gruppe.
In das Modell fügen wir nun noch zwei Rigid Transform-Blöcke und ein Solid-Block ein. Diese werden untereinander und mit dem Handgelenk-Sub-System verbunden wie in Bild 11 verbunden. Die Rigid Transform-Blöcke sind in der Frames and Transforms-Gruppe zu finden, der Solid-Block in der Body Elements-Gruppe.
 Hierbei muss auf die korrekte Verbindung der Anschlüsse (F und B) geachtet werden.
Hierbei muss auf die korrekte Verbindung der Anschlüsse (F und B) geachtet werden.
Der zuletzt eingefügte Solid-Block soll später in unserem Modell den Unterarm darstellen. Wir wollen daher seine Geometrie an die eines Unterarmes anpassen. Dies geschieht durch Doppeltklick auf den Block. Anschließend treffen wir die Einstellungen wie in Bild 12 dargestellt.
 Nun passen wir die Eigenschaften des linken Rigid Transform-Blocks folgendermaßen an (Bild 13).
Nun passen wir die Eigenschaften des linken Rigid Transform-Blocks folgendermaßen an (Bild 13).
 Gleiches führen wir für den rechten Rigid Transform-Block aus. Die Einstellungen entnehmen wir Bild 14.
Gleiches führen wir für den rechten Rigid Transform-Block aus. Die Einstellungen entnehmen wir Bild 14.
 Nun fassen wir die drei zuletzt eingefügten Blöcke (2x Rigid Transform, 1x Solid) zu einem Sub-System Unterarm zusammen. Dabei gehen wir vor wie beim Handgelenk-Sub-System:
Nun fassen wir die drei zuletzt eingefügten Blöcke (2x Rigid Transform, 1x Solid) zu einem Sub-System Unterarm zusammen. Dabei gehen wir vor wie beim Handgelenk-Sub-System:
- Markieren der Blöcke durch Ziehen eines Rechtecks mit gedrückter linker Maustaste
- Rechtsklick auf eines der markierten Objekte
- Auswählen von Create Subsystem from Selection
- Umbenennen in Unterarm
- eventuell Anpassen der Größe
Unser Modell sollte dann folgende Form besitzen (Bild 15).
 Da in unserem Modell der Ellbogen aus der gleichen Kombination von Blöcken wie das Handgelenk modelliert werden soll, können wir uns den modularen Aufbau unseres Modells durch Sub-Systeme zunutze machen. Wir kopieren zunächst das Sub-System: Rechtsklick auf das Sub-System Handgelenk, dann Copy auswählen, mit der rechten Maustaste auf einen freien Bereich im Modell klicken und Paste auswählen. Das standardmäßig als Handgelenk1 eingefügte Sub-System benennen wir durch Klicken auf den Namen um in Ellbogen. Anschließend wird der Unterarm mit dem Ellbogen verbunden (Bild 16).
Da in unserem Modell der Ellbogen aus der gleichen Kombination von Blöcken wie das Handgelenk modelliert werden soll, können wir uns den modularen Aufbau unseres Modells durch Sub-Systeme zunutze machen. Wir kopieren zunächst das Sub-System: Rechtsklick auf das Sub-System Handgelenk, dann Copy auswählen, mit der rechten Maustaste auf einen freien Bereich im Modell klicken und Paste auswählen. Das standardmäßig als Handgelenk1 eingefügte Sub-System benennen wir durch Klicken auf den Namen um in Ellbogen. Anschließend wird der Unterarm mit dem Ellbogen verbunden (Bild 16).
 Dieses Vorgehen (Kopieren, Einfügen, Umbenennen, Verbinden) wiederholen wir für weitere Subsysteme. Die weiteren Sub-Systeme und ihre äquivalenten Ursprungssysteme sind in der folgenden Tabelle dargestellt.
Dieses Vorgehen (Kopieren, Einfügen, Umbenennen, Verbinden) wiederholen wir für weitere Subsysteme. Die weiteren Sub-Systeme und ihre äquivalenten Ursprungssysteme sind in der folgenden Tabelle dargestellt.
| neues Sub-System | Kopie von |
|---|---|
| Oberarm | Unterarm |
| Schulter | Ellbogen |
| Rest | Oberarm |
Nachdem alle Sub-Systeme erzeugt ins Modell eingefügt wurden, sollte dieses aussehen wie in Bild 17.
 Wir wollen nun die Eigenschaften des Rest-Sub-Systems anpassen. Dazu öffnen wir dieses durch einen Doppeltklick darauf. Im Solid-Block ändern wir die z-Länge (der dritte Wert) von 0.4 auf 1.4, da dieser Block die Eigenschaften der Beine und des Rumpfes darstellen soll. In den beiden Rigid Transform-Blöcken des Rest-Sub-Systems ändern wir im Bereich Translation den Wert 0.2 auf 0.7 bzw. von -0.2 auf -0.7. Nun fügen wir (wieder per Drag & Drop) aus der SimMechanics Library noch einen Rigid Transform- und einen Solid-Block in das Rest-Sub-System ein. Der Solid-Block befindet sich in der noch geöffneten Body Elements-Gruppe, der Rigid Transform-Block in der Frames and Transforms-Gruppe. Den B-Anschluss verbinden wir mit der linken Seite (F-Anschluss) des linken Rigid Transform-Blocks, den F-Anschluss mit dem Solid-Block. Hierzu drehen wir den Rigid TRansform-Block einmal im Uhrzeigersinn (Rotate & Flip → ClockWise). Das resultierende Rest-Sub-System ist in Bild 18 dargestellt.
Wir wollen nun die Eigenschaften des Rest-Sub-Systems anpassen. Dazu öffnen wir dieses durch einen Doppeltklick darauf. Im Solid-Block ändern wir die z-Länge (der dritte Wert) von 0.4 auf 1.4, da dieser Block die Eigenschaften der Beine und des Rumpfes darstellen soll. In den beiden Rigid Transform-Blöcken des Rest-Sub-Systems ändern wir im Bereich Translation den Wert 0.2 auf 0.7 bzw. von -0.2 auf -0.7. Nun fügen wir (wieder per Drag & Drop) aus der SimMechanics Library noch einen Rigid Transform- und einen Solid-Block in das Rest-Sub-System ein. Der Solid-Block befindet sich in der noch geöffneten Body Elements-Gruppe, der Rigid Transform-Block in der Frames and Transforms-Gruppe. Den B-Anschluss verbinden wir mit der linken Seite (F-Anschluss) des linken Rigid Transform-Blocks, den F-Anschluss mit dem Solid-Block. Hierzu drehen wir den Rigid TRansform-Block einmal im Uhrzeigersinn (Rotate & Flip → ClockWise). Das resultierende Rest-Sub-System ist in Bild 18 dargestellt.
 Die Einstellungen des neuen Rigid Transform-Blocks ändern wir wie in Bild 19.
Die Einstellungen des neuen Rigid Transform-Blocks ändern wir wie in Bild 19.
 Der neue Solid-Block ist als Kugel ein einfaches Modell des Kopfes.
Um seine Eigenschaften anzupassen, ändern wir seine Einstellungen wie folgt (Bild 20).
Der neue Solid-Block ist als Kugel ein einfaches Modell des Kopfes.
Um seine Eigenschaften anzupassen, ändern wir seine Einstellungen wie folgt (Bild 20).

Modellierung der Regelung
Das Modell ist nun erstellt und wir können mit der Simulation beginnen. In dieser würde allerdings nicht viel geschehen, da noch keine Kräfte bzw. Bewegungen vorgegeben sind. Mit dem ![]() -Symbol gehen wir im Modell aus dem Sub-System Rest heraus. Nun wechseln wir durch Doppeltklick auf das Ellbogen-Symbol in dieses Sub-System und dort ebenfalls durch Doppeltklick in das Revolute Joint. Im Menu unter Actuation → Mode und Torque auswählen. Unter Sensing einen Häkchen bei Position und Velocity setzen.
-Symbol gehen wir im Modell aus dem Sub-System Rest heraus. Nun wechseln wir durch Doppeltklick auf das Ellbogen-Symbol in dieses Sub-System und dort ebenfalls durch Doppeltklick in das Revolute Joint. Im Menu unter Actuation → Mode und Torque auswählen. Unter Sensing einen Häkchen bei Position und Velocity setzen.
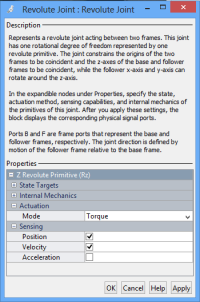 Hierdurch kann dem Gelenk ein Drehmoment vorgegeben werden und die Position und Geschwindigkeit ausgelesen werden. Nach Klicken auf OK erscheinen daher an dem Block zwei Ausgänge (q für die Position und w für die Geschwindigkeit) und ein Eingang (t für die Vorgabe des Drehmoments). Durch das Aufbringen eines Moments kann das Gelenk bewegt werden. Mit Hilfe der Sensorwerte aus den beiden Ausgängen, kann die Bewegung geregelt werden. Die Regelung legt dann wiederum fest, wie groß das wirkende Drehmoment ist.
Hierdurch kann dem Gelenk ein Drehmoment vorgegeben werden und die Position und Geschwindigkeit ausgelesen werden. Nach Klicken auf OK erscheinen daher an dem Block zwei Ausgänge (q für die Position und w für die Geschwindigkeit) und ein Eingang (t für die Vorgabe des Drehmoments). Durch das Aufbringen eines Moments kann das Gelenk bewegt werden. Mit Hilfe der Sensorwerte aus den beiden Ausgängen, kann die Bewegung geregelt werden. Die Regelung legt dann wiederum fest, wie groß das wirkende Drehmoment ist.
Die Modellierung der Regelung erfolgt in der Simulink-Umgebung. Durch Klicken auf das ![]() -Symbol kann diese gestartet werden. In der Simulink-Bibliothek wählen wir unter dem Reiter Simscape → Utilities. Wir erhalten die Ansicht von Bild 23.
-Symbol kann diese gestartet werden. In der Simulink-Bibliothek wählen wir unter dem Reiter Simscape → Utilities. Wir erhalten die Ansicht von Bild 23.
 Per Drag & Drop fügen wir zwei PS-Simulink Converter und einen Simulink-PS Converter ins Ellbogen-Sub-System. Mit Hilfe dieser Blöcke ist eine Signalumwandlung zwischen physikalischen Signal und der Simulink-Umgebung möglich. Die Ausgänge q und w des Revolute Joint werden jeweils mit der linken Seite eines PS-Simulink Converter verbunden. Anschließend fügen aus der Simulink Bibliothek unter (ganz oben) Simulink → Sources den Block Signal Builder ins Ellbogen-Sub-System ein. Mit Hilfe des Signal Builder kann ein Signal erzeugt werden. Durch Doppeltklick auf den Block kann das Signal angepasst werden. Voreingestellt ist ein Rechteck-Signal, das nur noch angepasst werden muss. In unserer Simulation soll nach zwei Sekunden die Bewegung des Klimmzugs beginnen und nach acht Sekunden wieder beendet werden. Hierzu ziehen wir im Schaubild die Kurve an der steigenden Flanke auf zwei Sekunden und die fallende Flanke auf acht Sekunden. Das Signal gibt den Verlauf des Sollwinkels des Ellbogen-Gelenks vor. Die Amplitude bestimmt den Zielwinkel während der Bewegung. Da wir einen Winkel von 150° erreichen wollen, müssen wir die obere horizontale Linie anklicken und im Y-Feld den Wert 2.61799 eingeben, da dieser Wert 150° in Radiant entspricht. Die Oberfläche des Signal Builders sollte nun so aussehen wie in Bild 24.
Per Drag & Drop fügen wir zwei PS-Simulink Converter und einen Simulink-PS Converter ins Ellbogen-Sub-System. Mit Hilfe dieser Blöcke ist eine Signalumwandlung zwischen physikalischen Signal und der Simulink-Umgebung möglich. Die Ausgänge q und w des Revolute Joint werden jeweils mit der linken Seite eines PS-Simulink Converter verbunden. Anschließend fügen aus der Simulink Bibliothek unter (ganz oben) Simulink → Sources den Block Signal Builder ins Ellbogen-Sub-System ein. Mit Hilfe des Signal Builder kann ein Signal erzeugt werden. Durch Doppeltklick auf den Block kann das Signal angepasst werden. Voreingestellt ist ein Rechteck-Signal, das nur noch angepasst werden muss. In unserer Simulation soll nach zwei Sekunden die Bewegung des Klimmzugs beginnen und nach acht Sekunden wieder beendet werden. Hierzu ziehen wir im Schaubild die Kurve an der steigenden Flanke auf zwei Sekunden und die fallende Flanke auf acht Sekunden. Das Signal gibt den Verlauf des Sollwinkels des Ellbogen-Gelenks vor. Die Amplitude bestimmt den Zielwinkel während der Bewegung. Da wir einen Winkel von 150° erreichen wollen, müssen wir die obere horizontale Linie anklicken und im Y-Feld den Wert 2.61799 eingeben, da dieser Wert 150° in Radiant entspricht. Die Oberfläche des Signal Builders sollte nun so aussehen wie in Bild 24.
 Solver
Durch Klicken auf das
Solver
Durch Klicken auf das ![]() -Symbol kann ein weiteres Signal hinzugefügt werden. Dies ist nötig, da im Gelenk zwei Werte gemessen werden. Wir fügen also ein zweites Signal zur Vorgabe der Winkelgeschwindigkeit hinzu. Da der Klimmzug unten bzw. oben nur gehalten werden soll und somit keine Bewegung statt findet, muss Signal 2 immer null sein. Nun können wir den Signal Builder mit einem Klick auf x oben rechts schließen.
-Symbol kann ein weiteres Signal hinzugefügt werden. Dies ist nötig, da im Gelenk zwei Werte gemessen werden. Wir fügen also ein zweites Signal zur Vorgabe der Winkelgeschwindigkeit hinzu. Da der Klimmzug unten bzw. oben nur gehalten werden soll und somit keine Bewegung statt findet, muss Signal 2 immer null sein. Nun können wir den Signal Builder mit einem Klick auf x oben rechts schließen.
Aus der Simulink Bibliothek holen wir nun (wieder per Drag & Drop) zwei Subtract-Blöcke in den Ellbogen. Diese sind dort unter Simulink → Math Operations zu finden. Die +Eingänge verbinden wir mit den Soll-Vorgaben aus dem Signal Builder. Die -Eingänge verbinden wir den umgewandelten Signalen aus den PS-Simulink Convertern (Bild 25).
 Als nächstes fügen wir zwei Gain-Blöcke ein, die ebenfalls unter Simulink → Math Operations sind. Die Eingänge der Gain-Blöcke verbinden wir jeweils mit den Ausgängen der Subtract-Blöcke.
Als nächstes fügen wir zwei Gain-Blöcke ein, die ebenfalls unter Simulink → Math Operations sind. Die Eingänge der Gain-Blöcke verbinden wir jeweils mit den Ausgängen der Subtract-Blöcke.
 Die Ausgänge der beiden Subtract-Blöcke verbinden wir wiederum mit den Eingängen eines Add-Blocks, den ebenfalls aus der Math Operations-Bibliothek in das Modell hinzufügen. Den Ausgang des Add-Blocks verbinden wir mit dem Eingang des Simulink-PS Converter, dessen Ausgang mit t des Revolute Joint. Das Modell sollte dann so aussehen wie auf Bild 27 dargestellt.
Die Ausgänge der beiden Subtract-Blöcke verbinden wir wiederum mit den Eingängen eines Add-Blocks, den ebenfalls aus der Math Operations-Bibliothek in das Modell hinzufügen. Den Ausgang des Add-Blocks verbinden wir mit dem Eingang des Simulink-PS Converter, dessen Ausgang mit t des Revolute Joint. Das Modell sollte dann so aussehen wie auf Bild 27 dargestellt.
 Die Gain-Blöcke verstärken das Signal am Eingang. Der Verstärkungsfaktor kann durch Doppeltklick auf den jeweiligen Gain-Block eingestellt werden. Der Gain-Block, der die Positionsdifferenz verstärkt, stellen wir auf 45, den der Winkelgeschwindigkeit auf 60.
Simulation
Durch Klicken auf den
Die Gain-Blöcke verstärken das Signal am Eingang. Der Verstärkungsfaktor kann durch Doppeltklick auf den jeweiligen Gain-Block eingestellt werden. Der Gain-Block, der die Positionsdifferenz verstärkt, stellen wir auf 45, den der Winkelgeschwindigkeit auf 60.
Simulation
Durch Klicken auf den ![]() -Button können die Parameter der Simulation angepasst werden. Wir wollen den Solver anpassen und wählen statt dem standardmäßigen ode45 (Dormand-Prince) den Solver ode15s (stiff/NDF). Dieser ist auch für steife Differentialgleichungen geeignet. Drücken von Apply und OK speichern die Einstellungen und schließen das Fenster
-Button können die Parameter der Simulation angepasst werden. Wir wollen den Solver anpassen und wählen statt dem standardmäßigen ode45 (Dormand-Prince) den Solver ode15s (stiff/NDF). Dieser ist auch für steife Differentialgleichungen geeignet. Drücken von Apply und OK speichern die Einstellungen und schließen das Fenster
Da sonst unnötige Fehlermeldungen auftauchen, löschen wir im Modell die zu Beginn in der Vorlage enthaltenen Blöcke Solid, Simulink-PS Converter, PS-Simulink Converter und Scope. Hierzu müssen wir zunächst aus dem Ellbogen-Sub-System in die oberste Ebene unseres Modells wechseln. Dieses sieht dann aus wie in Bild 29.

Durch Betätigen von ![]() starten wir nun die Simulation. Es öffnet sich automatisch ein Visualisierungsfenster von Matlab. Hier wird das Modell gezeigt.
starten wir nun die Simulation. Es öffnet sich automatisch ein Visualisierungsfenster von Matlab. Hier wird das Modell gezeigt.
Das fertige Modell kann hier heruntergeladen werden.
Anregungen für eigene Ideen
Nun kann mit dem erstellten Modell noch ein bisschen herumgespielt werden.Hier sind einige Anregungen:
- Erzeugen eines weiteren Moments im Schultergelenk, da der Mensch den Klimmzug nicht nur mit Bizeps/Armbeuger sondern auch unter Verwendung des Latissimus durchführt
- Vervollständigung des restlichen Körpers
- Erweiterung des Modells auf die dritte Dimension, mit der Verwendung von Kugelgelenken für Schulter und Hüfte
- Visualisierung einzelner Signale im Scope
- Verwendung realistischer Massen und Abmaße
- Testen welches Moment benötigt wird, um die Position in der oberen Stellung zu halten (Winkel-Stellung von 90° bzw. 150°)
</spoiler>
verfasst von Holger Dieterich & Andreas Döring
Ausblick
Die weiteren Möglichkeiten von SimMechanics sind nahezu grenzenlos. Es könnten beispieslweise die benötigten Kräfte für den Klimmzug ausgegeben werden. Dadurch könnten verschiedene Varianten miteinander verglichen werden (z.B. wie hoch die nötigen Momente bei einem Klimmzug mit einem engen Griff sich von der Variante mit weiten Griff unterscheiden) oder es kann berechnet werden, wie die Anthropometrie die notwendigen Kräfte beeinflusst.
Bevor solche Simulationen in Angriff genommen werden, sollte jedoch aufbauend auf das Tutorial, das 2D-Modell in ein 3D-Modell überführt werden. Ein Beispiel für ein 3D-Modell für den Klimmzug kann sich hier heruntergeladen werden. Bei dem vorgeschlagenen Modell entsprechen die Proportionen, Massen und Trägheitsmomente nicht der Realität. Diese können beispielsweise aus [2] bezogen werden. Der zip-Ordner enthält eine .slx-Datei, welche das 3D-Modell enthält und eine .m-Datei, indem die Auswertung statt findet. Bei der Simulation werden Werte im Scope gespeichert, mit denen zwei Plots erstellt werden. In der untenstehenden Abbildung ist der Momentenverlauf für den Ellbogen dargestellt (die Werte dürfen nicht mit realen Werten verglichen werden, da die Geometrie und die Massen des Modells nicht der Realität entnommen wurden).
Eine Auswertung kann ebenfalls für die Regelung gemacht werden. In der untenstehenden Abbildung ist der Soll-Ist-Vergleich des Winkels für das Ellbogengelenk dargestellt.
Das folgende Video zeigt das erstellte 3D-Modell. Das Video wurde mit Hilfe der Toolbox von SimMechanics erstellt.
Die Möglichkeit zur Visualisierung von den erstellten Modellen bietet einen großen Vorteil, so kann oft abgeschätzt werden, ob die gewünschte Bewegung abgebildet wurde.
Da die Bewegung des Menschen nicht über Momente in Gelenken entsteht, sondern über kontrahierende Muskeln, müsste das Modell weiter bearbeitet werden, indem Muskeln abgebildet werden, die lediglich translatorische Verschiebungen zu lassen.
Eine weitere Möglichkeit von SimMechanics ist, bestehende Modelle in Matlab/Simulink mit SimMechanics zu koppeln. Hier könnte z.B. stumpf die Position, Geschwindigkeit und Beschleunigung der Starrkörper vorgegeben werden, um lediglich die visuelle Ausgabe von SimMechanics zu nutzen. Es können aber auch die Modelle komplett in SimMechancis übertragen werden, um das Modell rein auf der physikalischen Ebene zu simulieren.
Bei dem Modellieren muss sich nicht auf den Klimmzug beschränkt werden, es kann auch die Kniebeuge modelliert werden, dies würde die Vorstufe zum Laufen darstellen. Um das Laufen abzubilden, müsste jedoch der Bodenkontakt modelliert werden. Dies könnte z.B. mittels einen Feder-Dämpfer realisiert werden, der immer dann eingeschaltet wird, wenn der Fuß in Kontakt mit dem Boden tritt.
Weiter gebe es in der Regelung Verbesserungspotential, z.B könnte der im Tutorial vorgestellte PD-Regler in einen PID-Regler erweitert werden. In dem Beispiel-3D Modell wurde dies umgesetzt, jedoch wurden die Werte nach keiner Literatur bestimmt. Eine weitere Verbesserung der Regelung würde die Verwendung von Zustandsräumen darstellen.
Einer der letzten Schritte der Modellierung, könnte die Bestimmung des effizientesten Ablaufs für eine bestimmte Bewegung sein.
verfasst von Andreas Döring
Fragen
<spoiler |1. Was sind die Vor- und Nachteile einer Simulation im Gegensatz zum Experiment? >Besseres Verstädnis von der Realität. Nachteil: es wird irgendwas modelliert.</spoiler>
<spoiler |2. Wozu dient eine Modellierung in SimMechanics? >Visualisierung, Erweiterung vorhandener Modelle.</spoiler>
<spoiler |3. Was sind die Vor- und Nachteile einer Simulation im Gegensatz zum Experiment? >Vorteil: besseres Verständnis von der Realität, Möglichkeit des paussierens während der Bewegung, Kostenersparnis, keine Gefahr für den Probanden. Nachteil: es können falsche Ergebnisse verwendet werden, nummerische Ungenauigkeiten, Simulation nur eine Annäherung. </spoiler>
<spoiler |4. Was ist Simscape? >Simscape ist ein Unterprogramm von Simulink. Mit Simscape können physikalische Systme nachmodelliert werden, z.B. Mechanik, Hydraulik, Pneumatik, Thermik, Magnetik und Elektronik. </spoiler>
Literaturverzeichnis
[1] MATLAB-Homepage, letzter Zugriff am 15. Juli 2015.
[2] Winter, David A. (2009). Biomechanics and Motor Control of Human Movement (4th Edition). New Jersey: John Wiley & Sons.


