Inhaltsverzeichnis
Animation
Um die, in der Simulation berechneten Ergebnisse, die bisher nur als Werte oder Graphen vorliegen, anschaulicher darzustellen, sollen diese durch eine Animation veranschaulicht werden. Die Beschreibung dieser Animation ist Gegenstand dieses Kapitels.
Ziel ist es, die Bewegung des Läufers mit Matlab als Animation darstellen zu können, um einen besseren Eindruck der Dynamik und des Verhaltens des Läufers zu bekommen.
Dafür werden in einem ersten Unterkapitel die Grundlagen der Animation beschrieben. Im zweiten Unterkapitel werden anschließend noch ausgewählte Animationen aufgezeigt.
Grundlagen
Um eine Animation der jeweiligen Modelle durchzuführen, müssen aus den einzelnen Simulationen die $x$- und $y$-Koordinaten des Körperschwerpunkts und des Fußes bzw. der Füße ausgelesen werden. Die Bewegung des Fußes in der Flugphase wird nicht berechnet wird, da diese für eine reine Betrachtung der Standphasen keine wichtige Rolle einnimmt. Sie würde einer einfachen Parabel mit Nachvornebringen des hinteren Fußes, ähnlich einem schiefen Wurfs, entsprechen. Ohne Betrachtung der Flugphase bleibt die $y$-Koordinate des Fußes also fest auf dem Wert der Bodenhöhe und es genügt, die $x$-Koordinate des Fußes jeweils bei einem neuen Aufsetzvorgang auszulesen. Betrachtet werden also die Bewegung des Körperschwerpunkts während der Stand- und Flugphase und die Position des Fußes bei einer Standphase.
Mittels des Simulink-Blocks ToWorkspace werden diese Koordinaten nach Beendigung der Simulation in den Workspace von Matlab geschrieben und stehen somit der weiteren Verarbeitung zu Verfügung.
Nachfolgend wird nun exemplarisch die Animation des Modells einbeiniges Laufen Schritt für Schritt erklärt. Die Animation der anderen beiden Modelle ist analog aufgebaut. Als Besonderheit ist bei der Animation des zweibeinigen Gehens zu beachten, dass es nun für jeden Fuß eine separate $x$-Koordinate gibt, die gezeichnet werden muss.

In Matlab können keine geometrischen Objekte erstellt werden. Sie müssen über die trigonometrischen Funktionen Punkt für Punkt gezeichnet werden. Mit diesen vier Variablen werden die Koordinaten der Kreise beschrieben, die als Ersatzsymbol für die Punktmasse und den Fuß verwendet werden.

Diesen wird anschließend über der Funktion fill eine gewisse Farbe gegeben. Der dritte Parameter gibt also die jeweilige Farbe der Masse oder des Fußes an. Durch diese Funktion wird ein graphisches Objekt erzeugt, welches nun durch seine Eigenschaften verändert werden kann. Somit muss das Objekt nicht bei jedem Bildaufbau neu erstellt werden, sondern es genügt, einzelne Paramater, zum Beispiel die $x/y$-Koordinaten anzupassen, und das Objekt zeichnen zu lassen.
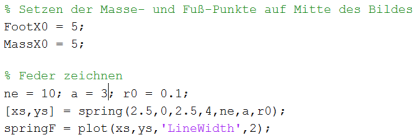
Als Visualisierung der Verbindung zwischen KSP und Fußpunkt dient eine Feder. Auch bei Systemen, in denen Dämpfer und Aktuatoren zum Einsatz kommen, beschränkt sich die Darstellung des gesamten Komplexes auf eine einzelne Feder, da die Animation sonst zu aufwendig werden würde. Die Feder wird über die Funktion spring erzeugt. Der Parameter $ne$ gibt die Anzahl der Windungen an, $a$ die Ruhelänge und $r_0$ den Radius der Feder. Wie bei den Punkten werden über die Funktion plot die Werte gezeichnet und in dem Objekt springF gespeichert.

Im Gegensatz zu den Masse- und FußpPunkten, die nur ihre Koordinaten verändern, muss die Feder nach jedem Bild neu gezeichnet werden, da sowohl ihre Position als auch die Länge variiert und die Form der Feder somit über die Funktion spring neu berechnet werden muss. Demgegenüber bleibt die Form der Masse- und Fußpunkte gleich und es genügt ein Anpassen der Koordinaten.

Anhand der Daten der Simulation wird nun die X/Y Position der Masse und die $x$-Position des Fußes angepasst. Die Variable $i$ stellt hierbei die Zeit dar.

Um zu verhindern, dass der Läufer auf der rechten Seite das Bild verlässt, wird überpüft, wann sowohl die $x$-Koordinate des Fußes und der Masse den rechten Bildrand ($x=10$) überschreiten. Dazu muss bei der Überschreitung des rechten Randes jeweils das Vielfache des Bildes abgezogen werden. Dies wird durch die Variable „ratio“ ermittelt, deren Wert anschließend von den Simulationswerten abgezogen wird. Dies entspricht der mathematischen Operation „modulo“. Diese kann aber nicht verwendet werden, da alle 4 Variablen immer gleichzeitig vom rechten zum linken Bildrand gesetzt werden sollen.

Da Fuß und Masse jeweils graphische Objekte sind, genügt es die $XY$-Koordinaten neu zu setzen. Daraufhin zeichnet Matlab automatisch die Kreise an die neue Stelle. Da nicht immer wieder alle Punkte neu berechnet werden, wird die Animation dadurch deutlich effizienter.

Bei der Feder hingegen ändert sich je nach Masse und Fußpunkt und Abstand zwischen diesen beiden die gesamte Feder. Deshalb muss die Feder bei jeder Iteration neu berechnet werden.

Zur Verdeutlichung der Federlänge wird diese je nach Zustand eingefärbt. Hierbei entspricht rot einer Stauchung, grün einer Ausdehnung und schwarz bedeutet, dass die Feder länger als die Ruhelänge ist.
Berechnet wird die aktuelle Federlänge currentL aus dem Abstand des Fußpunktes zum Massepunkt mit der Formel:
$$current_L=sqrt{(Foot_x - Mass_x)^2 + (Foot_y - Mass_y)^2}$$
Anschließend wird eine Fallunterscheidung gemacht, um die richtige Färbung herauszufinden. Dabei wird die aktuelle Länge der Feder zunächst mit der Ruhelänge $L_0$ verglichen. Ist die aktuelle Federlänge größer als $L_0$, so wird die Feder schwarz eingefärbt.
Sollte die Federlänge kleiner als die Ruhelänge sein wird überprüft, ob die aktuelle Federlänge größer oder kleiner als die vorheriger Länge ist. Über das Verhältnis der aktuellen Länge zur Ruhelänge wird zudem noch die Stärke der Kompression bzw. Ausdehnung visualisiert.
Videos
Folgende vier Animationen zeigen den Feder-Masse-Läufer in Aktion.
Aus dem Stand I
Aus dem Stand II
Laufen (Normal)
Laufen (Umfallen)
