Inhaltsverzeichnis
Laufen
Aus den drei Hauptkomponenten ergeben sich vier interessante Konstellationen, die simuliert und analysiert werden sollen:
- Ohne Aktuator - Ohne Dämpfer (nur die Feder wirkt als reines Feder-Masse-Modell)
- Mit Aktuator – Ohne Dämpfer
- Ohne Aktuator – Mit Dämpfer
- Mit Aktuator - Mit Dämpfer
Zunächst werden zu jeder dieser vier Varianten revevante Kraft- und Geschwindigkeitskurven aufgezeigt. Zudem werden die Parameter, die für ein erfolgreiches Laufen nötig sind, beschrieben und die Parametersuche kurz skizziert.
Anschließend erfolgt ein Vergleich der vier Konstellationen untereinander. Das Kapitel schließt mit einem Realitätsvergleich. Hierbei werden die gefundenen Simulationsergebnisse mit einem realen Marathonergebnis verglichen und analysiert.
Ohne Aktuator – Ohne Dämpfer
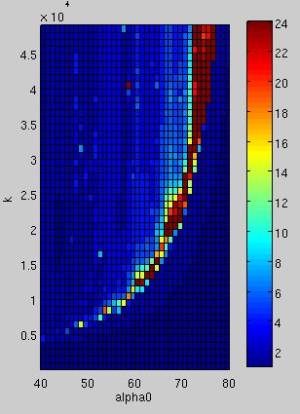
Mit der in Kapitel XXX beschriebenen Methode wurde der Landewinkel $\alpha_0$ und die Federkonstante $k$ variiert, um einen validen Parametersatz zu generieren. <imgref image1> zeigt zwei Bereiche, in denen das System erfolgreich 100 Schritte laufen kannt. Eine feinere Aufteilung der Simulationsschritte zeigt womöglich einen größeren gültigen Bereich um $alpha=69^\circ$ und $k=22.500 \frac{N}{m}$. Somit ergibt sich folgender passender Parametersatz:
$$v_{xy;0} =\begin{pmatrix} 5\frac{m}{s} \\ 0 \end{pmatrix} $$
$$x_{xy;0}=\begin{pmatrix}0 \\ 1 m \end{pmatrix} $$
$$\alpha_0 = 69^\circ $$
$$F=0 $$
$$b=1 $$
$$k=22.500$$
<imgcaption image1|Schrittanzahl in Abhängigkeit des Landewinkels α und der Federsteifigkeit k>
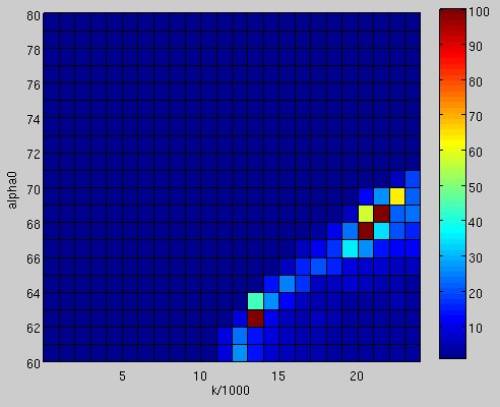 </imgcaption>
</imgcaption>
<imgref image2> zeigt die Veränderung der Position des Körperschwerpunktes (Punktmasse) über die Zeit in $x$-(oben) und $y$-Richtung (unten). Die Position der Punktmasse bewegt sich nahezu konstant linear mit der Anfangsgeschwindigkeit von 5 $\frac{m}{s}$. Die Position der Punktmasse in $y$-Richtung (Höhe) schwankt pro Laufzyklus von 0,89 bis 0,97 $m$. Somit erreicht die Punktmasse niemals die Ausgangshöhe von 1 $m$. Durch die Annahme, dass keine Energie verloren geht, wird die gesamte bei der Kompression in der Feder gespeicherte Energie wieder in die Ausdehnung der Feder übertragen. Somit ergibt sich eine nahezu identische Ausgangshöhe pro Zyklus.
<imgcaption image2|Veränderung der Position der Punktmasse in x-Richtung (oben) und y-Richtung (unten)>
 </imgcaption>
</imgcaption>
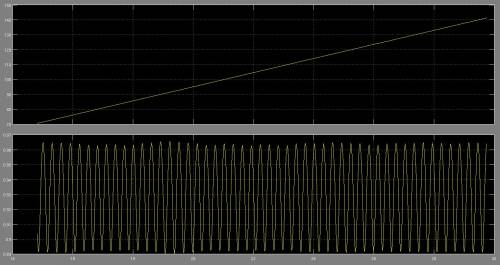
In <imgref image3> sind viele Laufzyklen dargestellt. Ein neuer Zyklus wird begonnen, wenn die Geschwindigkeit der Punktmasse in $y$-Richtung minimal wird. Hier setzt der der Läufer mit seinem Fuß auf. Beim Aufsetzen des Fußes wird die Feder gestaucht und somit die Geschwindigkeit in $y$-Richtung verlangsamt. Am unteren Umkehrpunkt (ca. -0.9) der $y$-Komponente ist die Feder maximal gestaucht und beginnt die gespeicherte Energie abzugeben und die Punktmasse zu beschleunigen. Dies zeigt sich in der zunehmenden Geschwindigkeit in $y$-Richtung. Die Feder scheint allerdings nicht die gesamte Energie zielgerichtet in die Vorwärtsbewegung (X-Komponente) umsetzen zu können und es entstehen kleine Schwankungen zwischen ca. 4,2 und 5,1 $\frac{m}{s}$.
Der Laufzyklus endet mit der höchsten Geschwindigkeit in $y$-Richtung.
<imgcaption image3|Geschwindigkeit in x- und y-Richtung von 4 Zyklen>
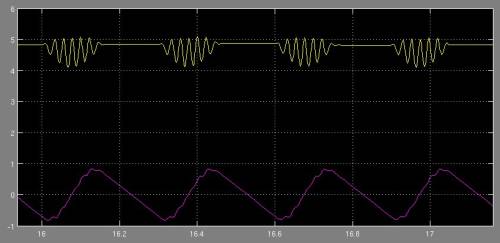 </imgcaption>
</imgcaption>
<imgcaption image4|Kraftkurve der Feder>
 </imgcaption>
</imgcaption>
<imgref image4> stellt die Kraftkurven der Bodenreaktionskräfte zweier Laufzyklen dar. Die $x$-Komponente ist in Lila eingefärbt, Rot stellt die $y$-Komponente dar. In der Flugphase nimmt die wirkende Bodenreaktionskraft der Feder in beide Richtungen den Wert Null an. Beim Aufsetzen des Fußes wird die Feder gestaucht und Energie in der Feder gespeichert. Die Federkraft verzögert als die Geschwindigkeit der Masse in $x$-Richtung. Dies zeigt sich in dem negativen Verlauf des lila eingefärbten Graphen. Ist der Tiefpunkt der Punktmasse erreicht, überholt die Punktmasse also den Fußpunkt, wird die potentielle Energie der Feder durch deren Ausdehnung wieder freigegeben. Die Punktmasse wird also in $x$-Richtung beschleunigt und somit steigt ist auch die Kraft wieder positiv. Anschließend sinkt die abgegebene Kraft wieder, der Fuß verlässt den Boden und der Zyklus ist beendet.
Die Kraftkomponente der Feder in $y$-Richtung hat immer einen positiven Wert, da die diese immer vom Boden weg entgegengesetzt der Punktmasse wirkt. Am Tiefpunkt der Masse (Umkehrpunkt) ist somit die Kraft am höchsten, da die Feder maximale gestaucht ist und nimmt ab, je weiter die Masse sich nach oben bewegt. Am Ende des Zykluses, zu Beginn der Flugphase ist die Kraft schließlich 0, da der Fuß abhebt und somit keine Bodenreaktionskräfte mehr auftreten.
<imgcaption image5|Landewinkel α pro Zyklus>
 </imgcaption>
</imgcaption>
<imgref image5> zeigt beispielhaft den Verlauf des Winkels zwischen Bein und Boden über mehrere Zyklen. Der Zyklus beginnt beim Aufkommen des Fußes mit einem Landewinkel von 69°. Das Bein dreht sich um den Aufsetzpunkt des Fußes und der Winkel wird dadurch größer. Ab einem Winkel von 90° beginnt die Abdrückphase des Zyklus, also die Phase, bei der die Masse in $x$-Richtung beschleunigt wird. Der Fuß verlässt den Boden bei ca 138°.
<imgcaption image6|Gegenüberstellung der Geschwindigkeiten (oben), Kraft (Mitte) und Winkel (unten)>
 </imgcaption>
</imgcaption>
<imgref image6> zeigt nochmal alle oben vorgestellten Kurven in einer Grafik zusammengestellt. Gut zu erkennen ist hierbei der Beginn eines Laufzyklus bei einem Winkel von 69°. Dies entspricht dem Beginn der Kraftkurven und zeitgleich einer minimalen Geschwindigkeit in $y$-Richtung. Gleichzeitig verändert sich die Geschwindigkeit in $x$-Richtung. Landewinkel 90° stellt den Beginn der Abdruckphase dar. Dies zeigt sich in der ab diesem Winkel positiven $x$-Komponente der Bodenreaktionskraft und dem Maximum der Kraftkomponente in $y$-Richtung. Ebenso hat die vertikale Geschwindigkeit der Punktmasse zu diesem Zeitpunkt den Wert Null, da hier der Wechsel von Verzögerungs- auf Beschleunigungsphase stattfindet.
Nur Aktuator bzw. nur Dämpfer
Für die beiden Konstellationen Laufen mit isoliertem Aktuator oder isoliertem Dämpfer konnten keine stabilen Parametersätze gefunden werden. Ein Dämpfer zieht Energie aus dem System heraus und schwächt somit die Amplitude der Feder immer weiter ab, sodass das System nach wenigen Schritten nicht mehr in der Lage ist zu stehen und somit umfällt.
Ein isolierter Aktuator erzeugt Kraft während der Kontaktphase. Dies führt zu einer Erhöhung der Energie der Abdruckphase. Auch hier ist es nicht möglich eine stabile Parameterkombination für 100 Schritte zu finden.
<imgcaption image7|Geschwindigkeits-, Kraft- und Winkelkurven mit Aktuator>
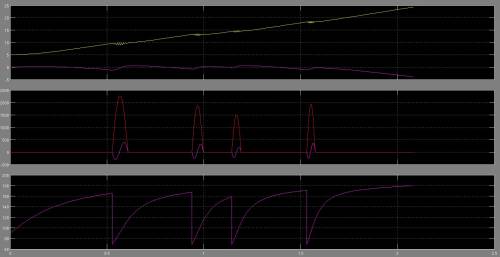 </imgcaption>
</imgcaption>
<imgref image7> zeigt die erreichten Schritte mit einem Aktuator von 1000 $N$. Anhand der Zykluszeit ist deutlich zu erkennen, dass das System keinen stabilen Zustand erlangt. Nach vier Schritten und ca. 2 $s$ wird die Simulation beendet, da die Punktmasse den Boden berührt.
Mit Aktuator - Mit Dämpfer
Für das Lauf-Modell mit Aktuator und Dämpfer wurde anhand des zu Beginn des Kapitels vorgestellten Skripts ein gültige Parameterkombination gefunden, die es ermöglicht 100 Schritte zu gehen. Gefunden wurde eine „stabile“ Lösung für den Aktuator mit dem Wert 2000 $N$ und für den Dämpfer 4740 $\frac{Ns}{m}$. <imgref image8> zeigt, dass die gültige Parameterkombinationen eine „Insellösung“ ist und nicht wie in <imgref image1> dieses Kapitels in ein Umfeld weiterer stabilen Kombinationen eingebettet ist.
<imgcaption image8|Gelaufene Schritte in Abhängigkeit von Aktuator und Dämpfer>
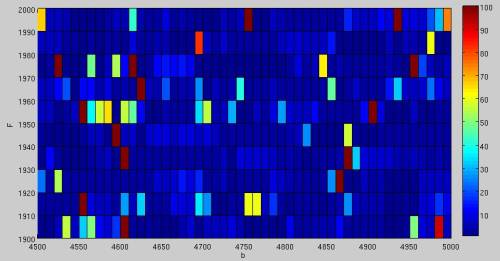 </imgcaption>
</imgcaption>
Die nachfolgende Abbildung zeigt die Anzahl der Schritte über die Zeit. Bemerkenswert ist hierbei die lange Verharrung bei ca. 3 Schritten bis 14 $s$ und das anschließend starke und nicht gleichmäßige Ansteigen auf 100 Schritte.
<imgcaption image9|Gelaufene Schritte über die Zeit.>
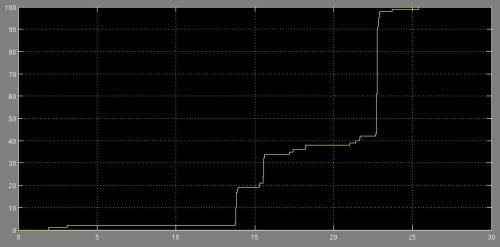 </imgcaption>
</imgcaption>
Die in <imgref image6> erläuterten Kurven ergeben für diese Parameterkombination keine geordneten klar zu deutenden Werte.
Die ersten drei Sekunden der Simulation zeigen dem Winkel $\alpha$ nach zu urteilen einen sehr langsamen Schritt, der wohl durch den starken Dämpfer so verzögert ist. In der Zwischenzeit hat die Kraft der Feder sich aufgebaut, um dann explosionsartig mit ca. 5000 $N$ zu wirken. Ab diesem Zeitpunkt bleibt der Landewinkel immer bei dem Startwinkel von 69°. Dies bedeutet, dass der Läufer keinen richtigen Schritt macht, sondern sofort bei dem Bodenkontakt bei gleichbleibendem Winkel den Boden verlässt.
Es zeigt sich, dass das alleinige Kriterium nach erfolgreich gelaufenen Schritten nicht aussagekräftig ist.
<imgcaption image10|Gegenüberstellung der Geschwindigkeit (oben), Kraft (mitte) und Winkel (unten)>
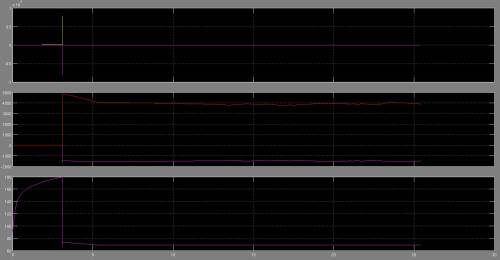 </imgcaption>
</imgcaption>
Vergleich der verschiedenen Konstellationen untereinander
Ein Vergleich der beiden Konstellationen ist aufgrund der nicht aussagekräftigen Simulation der zweiten Kombination nicht sinnvoll.
Vergleich mit Modellierung durch Geyer
Geyer (2005) erstellte ebenso ein laufendes Masse-Feder-Modell. Um die das eigene Modell zu validieren, wurde das Modell mit den von Geyer veröffentlichten Werten verglichen. Die nachfolgenden Abbildungen stellen die eigene Messung und Werte von Geyer gegenüber.
Abweichend von dem festgelegeten stabilen Kriterium von 100 Schritten wurde hier das Kriterium von Geyer (24 Schritte) verwendet, um eine bessere Vergleichbarkeit gewährleisten zu können. Der Vergleich zeigt eine hohe Übereinstimmung mit den veröffentlichten Daten.
<imgcaption image11|Stabile Regionen in Abhängigkeit von Landewinkel und Federsteifigkeit (eigene Simulation)>
 </imgcaption>
<imgcaption image12|Stabile Regionen in Abhängigkeit von Landewinkel und Federsteifigkeit (Geyer, 2005, S. 26)>
</imgcaption>
<imgcaption image12|Stabile Regionen in Abhängigkeit von Landewinkel und Federsteifigkeit (Geyer, 2005, S. 26)>
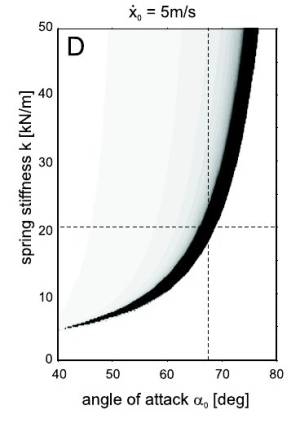 </imgcaption>
</imgcaption>
Vergleich mit der Realität
Nach Kiessling ergeben sich für einen Spitzenmarathonläufer die folgenden Werte:
- Endzeit: $2:10:20 h$
- Schrittlänge: $1,75 m$
- Frequenz: $180 \frac{Schritte}{min} = 3 \frac{Schritte}{s}$
- Geschwindigkeit: ca. $5,4\frac{m}{s}$
Aus der Simulation des Läufers als reines Masse-Feder-Modell ergeben sich nachfolgende Werte:
- Schrittlänge: $142\frac{m}{30 s} = 4,73 m$
- Frequenz: $100 \frac{Schritte}{30 s} = 3,3 \frac{Schritte}{s}$
- Geschwindigkeit: $5\frac{m}{s}$ (vorgegeben)
Der Vergleich der Werte zeigt, dass die Schrittfrequenz ungefähr der Realität entspricht. Dagegen ist die Schrittlänge mehr als das 2,5 x über dem realistischen Wert.
Literatur
Geyer H. (2005). Simple models of legged locomotion based on compliant limb behavior. PhD Thesis. Jena: Fakultät für Sozial- und Verhaltenswissenschaften.
