Inhaltsverzeichnis
MUS5 Muskel-Skelett
| Modul | MUS5 Muskel-Skelett-System |
|---|---|
| Kategorie | Muskel |
| Autor | Cengic, Rode |
| Voraussetzung | – |
| Bearbeitungsdauer | ca. 40 Minuten |
Lernziele
| Lehrveranstaltung | Lernziele |
|---|---|
| PS Biomechanik | - Wie funktioniert das MS-System? - Hebel kennen und verstehen - Funktion ein- bzw. zweigelenkiger Muskeln |
Einleitung
Hier könnt ihr euch in die Muskel-Skelett Modellierung einarbeiten. An einem einfachen Beispiel wird die Bedeutung der Geometrie veranschaulicht. Inhalte, die in diesem Wiki-Eintrag vermittelt werden sind zum Einen die auftretenden Hebelwirkungen im menschlichen Körper. Des Weiteren wird auf die biomechanische Muskelfunktion und Eigenschaften der Knochen eingegangen.
Muskel-Skelett-System
Unser Skelett ist ein Gebilde aus Knochen (s. Abb. Muskel-Skelett System), welches einen Rahmen für die Muskulatur bietet. Das Muskel-Skelett-System ist das Zwischenglied zwischen dem neuronalen System und dem mechanischen System, welche die Kraftentstehung und -übertragung auf die mechanische Umwelt beschreibt (Zschorlich, S. 87). Das Muskel-Skelett-System ermöglicht Fortbewegung, unseren Körper aufrecht zu halten, oder Organe zu schützen (z.B. schützt der Schädel das Gehirn).
Der Körper kann mechanisch als Segmentkette betrachtet werden, die durch Muskeln angetrieben wird. Durch elektrische Stimulation (Nerven), erzeugen die Muskeln Kräfte. Dadurch, dass Muskeln verschiedene Knochen verbinden (die durch Gelenke verbunden sind), erzeugen sie Drehmomente. Durch die Drehmomente kann die Segmentkette Bodenreaktionskräfte erzeugen (siehe unteres Bild), die zu Bewegung führen.
Die Hauptaufgabe des segmentierten Muskel-Skelett-Systems ist es, rotatorische Segmentbewegungen in translatorische Körperbewegung umzusetzen (vgl. van Ingen Schenau, 1989).
Beispiele für weitere Funktionen von Knochen und Muskeln:
Knochen
Knochen speichern Minerale und sind für die Bildung von Blutzellen zuständig. Insbesondere das Mineralsalz Kalzium wird für die Blutgerinnung und für die Ermöglichung des Querbrückenzyklus (Myosin-Aktin Interaktion) benötigt.
Muskel
Muskeln regulieren die Körpertemperatur und speichern Glykogen. Außerdem schütten sie als endokrines Organ über 400 verschiedene hormonähnliche Botenstoffe aus, die verschiedene Körperfunktionen beeinflussen. Dies ist Gegenstand aktueller Forschung.
Hebelwirkungen
Der menschliche Körper ist biomechanisch betrachtet eine Segmentkette bestehen aus Knochen und Gelenken. Durch Muskelanspannungen und -entspannungen werden die Gelenke gebeugt bzw. gestreckt.
Im Folgenden möchte ich drei Hebelklassen vorstellen. Jede Klasse ist für bestimmte Bewegungsabläufe geeignet:
- Hebelklasse: Kräfte treten beidseitig von der Drehachse auf (Schädel)
- Hebelklasse: Drehachse befindet sich an einem Ende des Hebels und die Kraft wirkt am anderen Ende (Gewicht liegt zwischen Drehachse und Hebelende → Schubkarre oder Achilles-Verse)
- Hebelklasse: Drehachse an einem Ende und das Gewicht am anderen Ende des Hebels. Die Kraft greift zwischen Drehachse und Gewicht an (Bizeps-Curls)
Schaut euch zunächst einmal folgendes Video an, um die drei Hebelklassen besser zu verstehen:
Mechanische Reichweite im Ellbogengelenk
Die absolute Reichweite körperlicher Bewegungen ist durch die mechanischen Eigenschaften der Gelenke limitiert. Verdeutlichen möchte ich dies am Beispiel der Ellbogengelenks.
Es kann maximal 180° gestreckt werden und nicht weniger als 15° gebeugt werden. Das Olecranon (proximales Ende der Elle) limitiert die Streckung und der Sehnenansatz des M. Brachialis verhindert die vollständige Beugung.
Tichauer vergleicht in seinem Paper Muskeln mit Zugfedern (vgl. S. 435). Ist der Muskel vollständig gebeugt, entfaltet dieser nur sehr geringe Kräfte (zusammengezogener Zustand der Zugfeder). In gestrecktem Zustand kann der Muskel jedoch nicht die maximale Kraft aufbringen (s. Kraft-Längen-Relation), da die Sarkomere überdehnt sind. Die potentielle Kraft variiert mit dem Grad der Flexion.
Exkurs: Gelenkmomente im Bein
Durch Drehmomente in den verschiedenen Gelenken kann der Mensch a) eine aufrechte Körperhaltung einnehmen und b) sich durch eine Transformation rotatorischer Bewegungen (um die Gelenke) in translatorische Bewegungen in seiner Umwelt Bewegen (Lokomotion).
Mit Hilfe eines vereinfachtes Beinmodells (nur Knie- und Hüftgelenk) wird gezeigt, welche Drehmomente in den Gelenken durch die Erdanziehung erzeugt werden (auch: inverse Statik). Um eine aufrechte Körperhaltung einzunehmen muss der Mensch diesen Momenten durch Muskelarbeit entgegenwirken. In diesem Modell wird eine Belastung von 800 N simuliert, die gehalten werden soll (isometrische Belastung).
Hinweis: positive Kniemomente deuten auf ein streckendes Drehmoment hin, negative Kniemomente auf ein beugendes Drehmoment. Die berechnete Muskelkraft bezieht sich ausschließlich auf den Kniestrecker.
|
erstellt mit GeoGebra von Dario Tokur |
Muskel-Gelenk-System
Über die Gelenke werden Muskelkontraktionen in Segmentbewegungen umgewandelt. Im menschlichen Körper gibt es verschiedene Muskel-Gelenk-Systeme: die eingelenkigen Muskeln und die zweigelenkigen Muskeln.
Eingelenkige Muskeln als kinetisches Element
Die Grundstruktur eines kinetischen Elements ist mit einem eingelenkigen Hebelsystem zu vergleichen. Jedes kinetische Element setzt sich zusammen aus folgenden 5 Bestandteilen (vgl. Tichauer, S. 437):
- Knochen
- Gelenke
- Muskeln
- Nerven
- Blutgefäße
Der Muskel kontrahiert nach dem Eintreffen von Aktionspotentialen (AP), welche über die Nervenbahnen (Axone) und -zellen übertragen werden. Eine motorische Einheit koordiniert mehrere Muskelzellen und leitet den elektrischen Impuls (AP) über die motorische Endplatte (synaptischer Spalt) an die Muskelzellen weiter. Bei der Muskelkontraktion wird ATP in ADP und ein weiteres Phosphat gespalten. So wird Energie freigesetzt und die Myosinköpfchen können sich wieder vom Aktinfilament lösen.
Bei diesem Vorgang der Energiefreisetzung wird Sauerstoff benötigt, welches durch Proteine (Hämoglobin) in den Erythrozyten (rote Blutkörperchen) transportiert wird. Schließlich nimmt das Myoglobin den transportierten Sauerstoff vom Hämoglobin auf und übergibt es an die Muskelzellen. Abfallprodukte, die während des Verbrennungsprozesses entstehen, werden über die venösen Blutbahnen abtransportiert.
Diese inneren Vorgänge bewirken die Bewegung der Hebel (Knochen) im Muskel-Skelett-System. Gelenke können gebeugt und gestreckt werden, da jeder Muskel (Agonist) einen Gegenspieler (Antagonist) hat.
Kinetische Elemente stellen den einfachsten Bewegungsvorgang in unserem menschlichen Körper dar. Komplizierter wird es bei mehrgelenkigen Muskelgruppen, welche in Form einer kinetischen Kette arbeiten.
Biomechanische Funktionen eingelenkiger Muskeln
Muskeln erfüllen spezielle, biomechanische Funktionen:
- Vermeidung von Kraftspitzen bei Stößen (low pass filter durch Sehnen)
- Energierückgewinnung (elastische Arbeitsweise durch Sehnen)
- Muskelkräfte verringern Zugspannung in Knochen infolge von Stößen (Stichwort - Spannbeton)
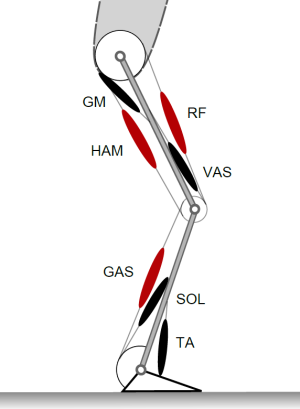
Zweigelenkige Muskeln
Zweigelenkige Muskeln zeichnen sich dadurch aus, dass sie über zwei Gelenke verlaufen. Das heißt, wenn der Muskel Kontrahiert bewegt er gleichzeitig zwei Körpersegmente.
Biomechanische Funktion zweigelenkiger Muskeln
Durch ihre Anordnung über mehrere Gelenke haben zweigelenkige Muskeln zusätzliche Funktionen:
- Energietransfer von proximal (körpernah, im Körperzentrum, z.B. Rumpf) nach distal (körperfern, an die Peripherie, z.B. Fuß)
- effiziente Anpassung von benötigten Drehmomenten in benachbarten Gelenken (ein Muskel erzeugt gleichzeitig Gelenkmomente in zwei Gelenken)
- sind geeignet, die Richtung der Bodenreaktionskraft einzustellen
Modell zweigelenkiger Muskeln
Um folgendes GeoGebra-Applet benutzen zu können, muss neben GeoGebra auch die Java Runtime Environment auf dem Rechner installiert sein. Um weitere Infos über die Einbindung von GeoGebra-Dateien zu erhalten, schaut euch folgendes HowTo an.
erstellt mit GeoGebra
In diesem GeoGebra-Modell kann untersucht werden, wie sich die Gelenkmomente in Abhängigkeit von der Segmentlänge legsegment und der Kraftrichtung alphaGRF der Bodenreaktionskraft (ground reaction force = GRF) ändern. Ebenso kann die Lage der Gelenke (Knie, Hüfte) geändert und die Auswirkungen beobachtet werden.
Abschlussvideo
Das abschließende Video behandelt noch einmal die zweigelenkigen Muskeln (hier der Knieapparat).
Zusammenfassung
Im letzten Modul wurde ein Zusammenhang zwischen den Muskeln und den zu bewegenden Knochen, bzw. dem ganzen Skelett hergestellt. Um zu verstehen wie Muskeln ein Skelett bewegen, habt ihr Hebelwirkungen und das Muskel-Gelenk-System kennengelernt. Darin spielten eingelenkige und zweigelenkige Muskeln eine Rolle.
Fragen
<spoiler |1. Beschreibe die Funktion der ein- und zweigelenkigen Muskeln!>
Ein eingelenkiger Muskel hat die Funktion zwei Segmente, die über ein Gelenk miteinander verbunden sind, relativ zueinander zu bewegen. Zudem erfüllt er, wie oben aufgeführt, noch folgende biomechanische Funktionen: Vermeidung von Kraftspitzen bei Stößen, Energierückgewinnung durch elastische Arbeitsweise von elastischen Struktur (z.B. Sehnen), Verringerung der Belastung im Knochen.
Im Gegensatz dazu ist der zweigelenkige Muskel über 2 Gelenke 'gespannt', er bewegt also 2 nicht benachbarte Segmente relativ zueinander. Durch diesen Aufbau hat er zusätzlich folgende Funktionen: Energietransfer zwischen den Gelenken (z.B. von proximal zu distal), Ausgleich von Drehmomenten in benachbarten Gelenken, Einstellung der Richtung der Bodenreaktionskraft.
</spoiler>
<spoiler |2. Erkläre die Muskelfunktion bei einer aktiven Beinstreckung! Wie kommt die Streckung des Beines zustande?> Zu einer Beinstreckung kommt es dann, wenn sich der Streckermuskel, z.B. der Kniestrecker (quadriceps femoris) kontrahiert. </spoiler>
<spoiler |3. Welche Hebelklassen gibt es und wodurch sind sie gekennzeichnet?> Es gibt drei verschiedene Hebelklassen. Sie unterscheiden sich alle in der Anordnung von Drehachse, Kraft und Last (Gewicht). Bei Hebeln, die zur 1. Klasse gehören, befindet sich die Drehachse zwischen Kraft und Last. Die 2. Hebelklasse kennzeichnet sich dadurch aus, dass sich die Drehachse am einen Ende des Hebels befindet und die Kraft am anderen Ende. Die Last liegt dazwischen. Bei der 3. Hebelklasse liegt die Drehachse ebenfalls am einen Ende, die Last allerdings am anderen und die Kraft greift zwischen Drehachse und Last an. </spoiler>
<spoiler |4. Wie kann in einem Bein die Kraft in Betrag und Richtung eingestellt werden?> - in Bearbeitung - </spoiler>
Literatur
G.J. van Ingen Schenau. From rotation to translation: constraints on multi-joint movements and the unique action of bi-articular muscles. Human Movement Science, 8(4):301–337, 1989.
Zschorlich, V. (1987). Elektromyographie und Dynamometrie in der Bewegungsforschung. Ein systemanalytischer Ansatz zur Untersuchung der Bewegungskoordination. Hamburg: Czwalina.