Inhaltsverzeichnis
MMB1 Kinemetrie
| Modul | MMB1 Kinematik-Messung |
|---|---|
| Kategorie | Messmethoden Biomechanik |
| Autor | Cengic |
| Voraussetzung | Grundlagen Biomechanik |
| Bearbeitungsdauer | ca. 45 Minuten |
| Letzte Änderung | 26. Nov 2014 |
| Status | in Bearbeitung |
| Lehrveranstaltung | Lernziel |
|---|---|
| PS Forschungsmethoden 2 | - Was ist Kinemetrie und was misst sie? - Körperachsen und Ebenen - Welche Methoden gibt es? - Welchen Mehrwert für die Wissenschaft wird erzielt? |
Einleitung
Aus mechanischer Sicht versteht man unter der Bewegung eines Punktes oder eines Körpers die Ortsveränderung über die Zeit. Neben räumlich-zeitlichen Ausprägungen (Kinematik) können auch die verursachenden Mechanismen (Dynamik) von Interesse sein. In diesem Modul wird behandelt wie die kinematischen Grundgrößen gemessen werden können und welche Herausforderungen dahinter stecken.
Grundbegriffe
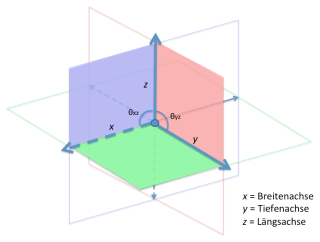
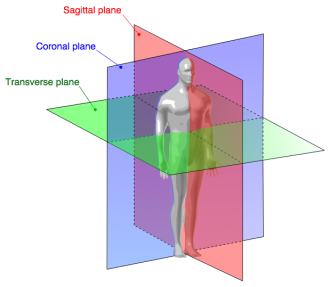
Der menschliche Körperschwerpunkt ist definiert durch den Schnittpunkt der drei Körperachsen: Körperbreitenachse, Körpertiefenachse und Körperlängsachse. Spannt man diese Achsen zu Ebenen auf, ergeben sich die drei Körperebenen (s. Abb. 1 & 2):
- Frontalebene (Achsen x-z: medio-lateral und vertikal; blau)
- Sagittalebene (Achsen y-z: antero-posterior und vertikal; rot)
- Transversalebene (Achsen x-y: medio-lateral und antero-posterior; grün)
Zur Bestimmung der räumlich-zeitlichen Ausprägung einer Bewegung eignen sich Koordinatensysteme. Für die Darstellung in 3D wird i.d.R. das kartesisches Koordinatensystem verwendet. Dieses besteht aus normal aufeinander stehenden Achsen (s. Abb. 1). Des Weiteren kann ein Koordinatensystem global (ortsfest) oder lokal (bewegtes KS) sein.
Die Beschreibung der kompletten Kinematik eines Körpersegments erfordert 15 Parameter in Abhängigkeit zur Zeit (Winter, 2009, S. 47f.):
- Position ($x, y, z$) des Körperschwerpunktes
- Lineare Geschwindigkeit ($\dot{x}, \dot{y}, \dot{z}$) des Körperschwerpunktes
- Lineare Beschleunigung ($\ddot{x}, \ddot{y}, \ddot{z}$) des Körperschwerpunktes
- Winkel ($\theta_{xz}, \theta_{yz}$)
- Winkelgeschwindigkeit ($\omega_{xz}, \omega_{yz}$)
- Winkelbeschleunigung ($\alpha_{xz}, \alpha_{yz}$)
Die Angabe eines dritten Winkels ist redundant. Zwei Winkel sind ausreichend zur Beschreibung einer Rotation um den Körperschwerpunkt.
<spoiler|Wie viele Parameter werden benötigt für die Beschreibung aller Körpersegmente?>
Anzahl der Körpersegmente = Füße + Unterschenkel + Oberschenkel + Rumpf + Kopf + Oberarme + Unterarme & Hände = 12 Segmente
Parameteranzahl = 15 x 12 = 180
</spoiler>
Kinemetrische Methoden
„Unter Kinemetrie versteht man die Erfassung, Analyse und Darstellung kinematischer Merkmale bei Haltungen und Bewegungen“ (Schwameder, 2009, S. 88). Bei der Erfassung kinematischer Merkmale stehen dem Biomechaniker zwei Möglichkeiten zur Verfügung, die direkte und die indirekte Methode. Im Folgenden wird erstere Methode näher ausgeführt.
Direkte Methoden
Zu den direkten kinemetrischen Methoden zählen (vgl. Schwameder, 2009, S. 92ff.):
| Methoden | Was? | Wie? |
|---|---|---|
| Zeitmessung | Stütz- und Flugzeiten beim Sprint | Stoppuhren, elektronische Kontaktschalter oder –matten, Lichtschranken, Videobildanalyse |
| Weg- und Geschwindigkeitsmessung | 100m-Sprint | Seilzug, LAVEG, Radar- oder GPS-Systeme, elektro-optische Systeme |
| Winkelmessung | Kniewinkel | Winkelmesser, Drehpotentiometer |
| Beschleunigungsmessung | Sprintstart vom Starblock | Akzelerometer |
| Positions- und Richtungsmessung | Ski-Alpin | Elektronische Intertialsysteme (IMU) in Verbindung mit GPS |
Das Laser-Messverfahren LAVEG wird im Abschnitt Anwendungen ausführlich vorgestellt.
Indirekte Methoden
Bei den indirekten Messmethoden werden Bewegungen zunächst aufgezeichnet. Die gemachten Aufnahmen können zur späteren Bewegungsanalyse herangezogen und verarbeitet werden. Eine numerische Erfassung der Bildkoordinaten erfolgt durch manuelles Anklicken oder automatisches Tracking, nachdem Bild- und Raumkoordinaten der relevanten Objektpunkte in Beziehung gesetzt wurden (vgl. Schwameder, 2009, S. 95).
In Abhängigkeit der Fragestellung muss das Aufnahmegerät (z.B. Kamera) voreingestellt sein. Neben dem räumlich-zeitlichen Auflösungsvermögen der Mess-Systeme, ist eine passende Belichtungszeit zu wählen. Der menschliche Fuß legt z.B. bei einer Geschwindigkeit von 6 m/s in einem Belichtungsfenster von 1/1000 s einen Weg von 6 mm zurück. Ebenso muss bei videometrischen Aufnahmen die Anzahl an Dimensionen (2D, 3D) gewählt werden. Mehr dazu findet ihr in MMB05 Elektro-Optik.
Datenverarbeitung
Datenauflösung
Die Genauigkeit kinematischer Daten ist abhängig von der zeitlichen bzw. räumlichen Auflösung (Schwameder, 2009, S. 99f.).
Anders gesagt sind die zeitliche und räumliche Auflösung die kleinsten diskreten Werte, die ein Messinstrument aufnehmen kann.
Zeitliche Auflösung
Die zeitliche Auflösung bezeichnet i.d.R. die Aufnahmefrequenz des jeweiligen Messinstruments. Es gibt keine ideale zeitliche Auflösung, diese muss in Abhängigkeit der Fragestellung entsprechend gewählt werden. Für die klinische Ganganalyse sind 50 Hz (50 Messungen pro Sekunde) ausreichend, während beim Tennis der Ballkontakt mit High-Speed Kameras nachverfolgt werden muss; dabei wird für jede Messung ein Wertepaar erzeugt.
Räumliche Auflösung
Bei elektronischen Datenaufnahmesystemen ist die Auflösung des AD-Wandlers ein limitierender Faktor. Analoge Signale werden hier in speicherfähige digitale Signale umgewandelt. Ein 12-bit-Wandler kann ein Messignal in $2^{12}$ ($=4096$), gleich große Teile auflösen. Für ein Goniometer ist diese Auflösung ausreichend, da der aufgelöste Winkel um maximal $0,04°$ ($=\frac{180°}{4096}$) abweichen kann. Die Bestimmungsgenauigkeit von Videodaten im PAL-Format (768 x 576 px) beträgt bei einem Bildausschnitt von 4×3 m ca. 5,2 mm. Aus diesem Grund bietet es sich an, bei biomechanischen Aufnahmen den Bildausschnitt groß zu wählen.
Die räumliche Auflösung beschreibt also die Untergrenze, bei der eine Bewegung als solche in einem optischen System erkannt werden kann. Je höher die Auflösung des verwendeten Geräts, desto tiefer kann die Untergrenze liegen.
Fehler
Grundsätzlich kann in zwei Fehlerarten unterschieden werden: Systematischer bzw. zufälliger Fehler (vgl. Schwameder, 2009, S. 101).
Systematische Fehler treten bei unveränderten Messbedingungen stets mit dem gleichen Wert auf. Sie sind objektiv bedingt durch die Unvollkommenheit der Messgeräte und Messmethoden. Durch genauere Messgeräte und Messverfahren sind diese Fehler jedoch zu ermitteln und können damit korrigiert werden. Ein systematischer Fehler kann durch eine fehlerhafte Optik der Kamera oder mangelhafte mathematische Algorithmen charakterisiert sein.
Zufällige Fehler werden durch nicht voraussehbare Veränderungen der Messbedingungen oder durch die Fähigkeiten des Beobachters (subjektive Fehler) hervorgerufen. Sie entstehen bei elektronischen Systemen bei der Punkterfassung (z.B. automatisches Tracking) oder aufgrund räumlich unzureichender Auflösung der Mess-Systeme.
Anwendungen
LAVEG
Das LAVEG-System zählt zu den Lasermessverfahren und wird sowohl im Straßenverkehr, als auch im Sport verwendet. In regelmäßigen Abständen wird ein Laserimpuls von der Messstation ausgesendet, vom Messobjekt reflektiert und wieder aufgefangen. Da die Lichtgeschwindigkeit bekannt und konstant ist, kann die Distanz des Messgerätes zum Messobjekt kann durch Laufzeitmessung bestimmt werden.
;#;
$Entfernung\ =\ \frac{1}{2}* 300.000.000 \frac{m}{s}*t_{LICHT}$
;#;
<spoiler|Berechne die Laufzeit $t_{LICHT}$ für eine Entfernung von 20 m>
$t = 2*\frac{20 m}{300.000.000 \frac{m}{s}} = 1,33 * 10^{-7} s$
</spoiler>
Bei mindestens zwei solcher Distanzmessungen in einem bestimmten Zeitfenster kann die mittlere Geschwindigkeit berechnet werden. Tatsächlich werden nach dem Auslösen des Messintervalls nicht nur 2, sondern rund 200 Messungen in einem Zeitraum von 0,36 s durchgeführt.
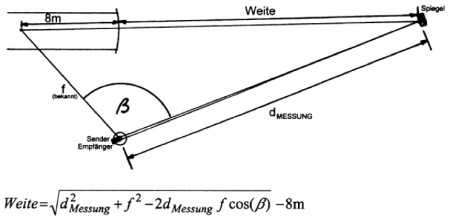
Triangulation beim Speerwurf
In der Realität kann der Messposten nie genau in Fahrt-/Laufrichtung des Messobjekts stehen. Die Messung erfolgt entweder schräg von der Seite, oder schräg von oben bei Messungen von Brücken. Beim Speer-, Diskus- und Hammerwurf kann die Wurfweite mittels von Triangulation berechnet werden (s. Abb. 3).
Die Formel für die Wurfweite wird im MMB1-Tutorial näher ausgeführt.
Elektro-optische Systeme
Die mit optischen Verfahren numerisch erfassbaren Größen sind die kinematischen Grundgrößen Länge bzw. Winkel und die Zeit. Sämtliche andere Größen, insbesondere die kinematischen Größen Geschwindigkeit und Beschleunigung, sind deren abgeleitete Größen. Der wesentliche Vorzug (elektro-) optischer Messverfahren besteht in der Möglichkeit der weitgehend rückwirkungsfreien Messung von Haltungen und Bewegungen. Der Begriff „Rückwirkung“ bezeichnet hier einen durch die Messung auf das Messobjekt wirkenden Einfluss (vgl. Baumann & Preiß, 1996, S. 88).
Eine detailliertere Ausführung über die Nutzung und Anwendung (elektro-)optischer Systeme findet sich hier.
Zusammenfassung
Fragen
<spoiler|Welche Ebenen gibt es in der Kinemetrie und wie sind sie angeordnet?>Es gibt drei Achsen, diese sind die Sagittal-, Transversal- und Frontalebene. Sie sind alle orthogonal zueinander angeordnet. Die Frontalebene beschreibt eine Sicht von „vorne“ auf das Objekt, die Sagittaleben von der „Seite“ und die Transversalebene von „oben“.</spoiler> <spoiler|Welche Messmethoden können in einer direkten Methode Anwendung finden?>Direkte Methoden sind zum Beispiel Wegmessung und Geschwindigkeitsmessung, da hier direkt das Resultat gemessen werden kann.</spoiler> <spoiler|Was ist der wesentliche Unterschied zwischen direkten und indirekten Methoden bei kinemetrischen Messungen?>Bei direkten Methoden wird das erzielte Resultat gemessen, bei indirekten Methoden basierend aus den Messungen unmittelbar vor dem Resultat auf dieses geschlossen.</spoiler> <spoiler|Wie sind die Begriffe zeitliche und räumliche Auflösung zu verstehen?>Die Begriffe beschreiben den minimalen Abstand zwischen zwei Wertepaaren. Anhand eines optischen Systems lassen sich beide Begriffe recht anschaulich machen: Die zeitliche Auflösung ist die Zeit zwischen zwei Aufnahmen, während die räumliche Auflösung auf diesen beiden Bildern als diskrete Bewegung auszumachen ist.</spoiler> <spoiler|Was ist der Unterschied zwischen systematschen und zufälligen Fehlern bei Messgeräten?>Systematische Fehler treten aufgrund der Unvollkommenheit der Messinstrumente regelmäßig und gleichmäßig auf, und können durch präzisere Messungen korrigiert werden. Zufällige Fehler treten unerwartet auf und haben ihren Ursprung in den Veränderungen der Messumgebung oder menschlichen Einflüssen.</spoiler>
Literatur
Baumann, W. & Preiß, R. (1996). Biomechanische Meßverfahren. In R. Ballreich & W. Baumann (Hrsg.). Grundlagen der Biomechanik des Sports (S. 75-102). Probleme, Methoden, Modelle. Stuttgart: Ferdinand Enke Verlag.
Schwameder, H. (2009). Einführung in die Kinemetrie. In A. Gollhofer (Hrsg.), Handbuch Sportbiomechanik (S. 88-103). Schorndorf: Hofmann.
Seyfarth, A. (2012). Kinemetrie - Entfernung. Laveg - Lichtweg. Präsentationsfolien im Rahmen des PS Messwertaufnahme und -verarbeitung SS 2012. Darmstadt: Institut für Sportwissenschaft.
Unfallanalyse Berlin. Polizeiliche Geschwindigkeitsmessung am Beispiel des Laser-Messgeräts LAVEG. Zugriff am 16. November 2014 unter http://www.unfallanalyse.de/unfallrekonstruktion/radar.html.
Winter, D. (2009). Biomechanics and Motor Control of Human Movement. Hoboken, New Jersey: John Wiley & Sons, Inc.