Inhaltsverzeichnis
Laufen
Der Modus 2 (Laufen) umfasst in dem hier entwickelten Modell eine Punktmasse, die an einen Feder-Dämpfer-Aktuator-Komplex, angebracht ist:
<imgcaption image1|Feder-Dämpfer-Aktuator-Komplex>
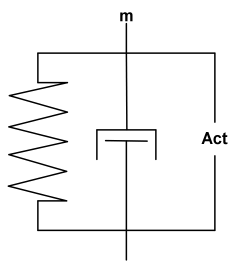 </imgcaption>
</imgcaption>
Die Grundlage für die konzeptionelle Entwicklung dieses Feder-Dämpfer-Aktuator-Komplexes war das von Hill vorgestellte Muskelmodell. Dieses umfasst als Muskelpendant ein kontraktiles Element CE und kombiniert dieses mit einem dazu parallelen kontraktilen Element CEE. Um die Eigenschaften der Sehne zu in das Modell zu integrieren wird zusätzlich dazu ein seriell geschaltetes, kontraktiles Element SEE hinzugefügt.
<imgcaption image2|Muskelmodell von Hill (entnommen aus Seyfarth & Rinderknecht (2012), S. 10)>
 </imgcaption>
</imgcaption>
Die Idee, eine Kombination aus CE und PEE zur Modellierung des Muskels zu verwenden, wurde aus Hills Modell übernommen. Auf das seriell elastische Element wurde im Modus Laufen verzichtet. Zusätzlich wurde dem Modell mit einem, zu CE und PEE parallel geschalteten Dämpfer, ein weiteres Element hinzugefügt.
Integrator
Der Integrator bildet den Kern jeder Simulation und dient der Berechnung der aktuellen Geschwindigkeits- und Ortswerte. Hierfür werden sowohl die Vektoren der Startgeschwindigkeit ($v_0$) ,der Startposition ($x_0$), sowie der Erdbeschleunigung ($g$) und ggf. die Geschwindigkeitszunahme ($v_xplus$) in x-Richtung als Eingangsparameter benötigt. Für die erstmalige Berechnung der Geschwindigkeits- und Ortswerte werden die Startparameter verwendet, für alle folgenden Integrationen werden dann die jeweils aktuell berechneten Werte herangezogen.
Im ersten Schritt des Integrators wird von dem Vektor der aktuellen Beschleunigung, der sich aus einer separaten Kraftberechnung ergibt, der Vektor der Erdbeschleunigung subtrahiert und es ergibt sich der Vektor der Gesamtbeschleunigung der Punktmasse:
$$\begin{pmatrix}a_{x;ges}&a_{y;ges}\end{pmatrix}=\begin{pmatrix}a_x&a_y\end{pmatrix} - \begin{pmatrix}0&g\end{pmatrix}$$
Im Anschluss wird die aktuelle Geschwindigkeit durch die Integration dieser Beschleunigung berechnet. Als Startwert für diesen Integratorblock dient der, in den Anfangsbedingungen vorgegebene Vektor der Anfangsgeschwindigkeit $v_0$. Die aktuell berechnete Geschwindigkeit wird in einem weiteren Schritt ggf. durch die zusätzliche Geschwindigkeit in x-Richtung ($v_xplus$), deren Berechnung bereits im Kapitel „Rampe“ beschrieben wurde, ergänzt. Der aktuelle Geschwindigkeitsvektor ergibt sich also zu:
$$\begin{pmatrix}v_{x;ges}&v_{y;ges}\end{pmatrix} = \begin{pmatrix}v_x&v_y\end{pmatrix} + \begin{pmatrix}v_xplus&0\end{pmatrix}$$
Dieser wird in einem weiteren Integratorblock zum jeweils aktuellen Positionsvektor integriert. Als Anfangsbedingung für diese Integration dient der, in den Startparametern vorgegebene Vektor der Anfangsposition der Punktmasse.
<imgcaption image3|Blockschaltbild des Integrator-Subsystems des Modus Laufen>
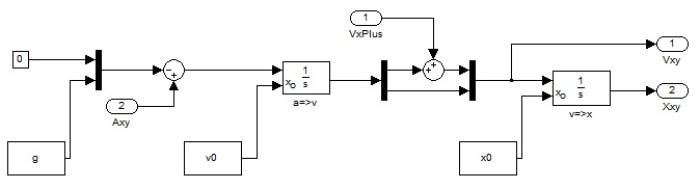 </imgcaption>
</imgcaption>
Die in diesem Integratorschaltbild berechneten Vektoren der Beschleunigung, der Geschwindigkeit und der Position sind die essentiellen Grundlagen für alle Berechnungen der Simulationen und werden daher durch Ausgänge in übergeordnete Systeme/Subsysteme ausgegeben.
Landehöhen
Damit der Integrator die aktuellen Geschwindigkeits- und Ortswerte pro Schritt berechnen kann, muss klar definiert werden, wie und wann ein Schritt beendet ist und ein neuer Integrationsschritt beginnen muss. Hierfür werden die Landehöhen berechnet.
Da die im Integrator berechneten Positionsvektoren ausschließlich die Lage der Punktmasse angeben, jedoch nicht die Position des Fußes, die für andere Berechnungen benötigt wird (Zeitpunkt des Bodenkontakt, Beginn einer neuen Standphase, Kraftberechnung,…), müssen diese in einem weiteren Subsystem berechnet werden. Die Berechnung der Fußposition findet im Subsystem „Landehöhen“ statt. Bei der Berechnung der Landehöhen werden als Eingangsparameter der Landewinkel ($\alpha_0$) und die Ausgangslänge ($L_0$) der Feder benötigt, die für jedes Aufkommen des Fußes als konstant angenommen und in den Startparametern vorgegeben werden. Auf der Basis dieser beiden festgelegten Größen lässt sich ein eindeutiges Kriterium definieren, welches das Erkennen eines Bodenkontakts des Fußes und somit einer neuen Standphase ermöglicht.
<imgcaption image4|Darstellung des Schritt-Kriteriums>
 </imgcaption>
</imgcaption>
Als Beginn einer neuen Standphase sei der Zeitpunkt des ersten Bodenkontakts der Feder definiert. Dieser Zeitpunkt lässt sich aus der Ausgangslänge der Feder und dem Landewinkel berechnen. Eine Standphase beginnt, sobald die Höhe der Punktmasse die Landehöhe erreicht, bzw. der y-Wert des Fußes den Wert Null annimmt. Die Berechnung der Landehöhe ($y_L$) wird in Abb. 4 ersichtlich und lautet wie folgt:
$$y_L = L_0 * sin(\alpha_o*\frac{\pi}{180})$$
Neben der Landehöhe $y_L$ soll auch noch der x-Wert der Position $x_L$ des Fußes während einer Standphase berechnet werden. Dieser wird in weiteren Berechnungen, wie beispielsweise bei der Kraftberechnung, in der die Feder um den Fußpunkt dreht, benötigt. Die Berechnung erfolgt auf ähnliche Weise und ist wie folgt definiert:
$$x_L = L_0 * cos(\alpha_o*\frac{\pi}{180})$$
Das Blockschaltbild des Subsystems „Landehöhen“ wird in Abb. 5 dargestellt:
<imgcaption image5|Simulink-Diagramm des Subsystems Landehöhen>
 </imgcaption>
</imgcaption>
Nachdem das Kriterium für eine neue Standphase definiert ist, muss das laufende System anhand dieses Kriteriums ständig überprüft werden. Diese Überprüfung findet im Subsystem „Fuss“ statt.
Fußpunktberechnung
Das Subsystem „Fuss“ erhält als Eingangsparameter sowohl die aktuelle Position $x_{xy}$ der Masse, die bereits im Subsystem Integrator berechnet wurde, als auch die berechneten x- und y-Koordinaten des Subsystems Landehöhen. In diesem Subsystem werden sowohl die lokalen Werte der Fussposition, als auch die globalen Werte. Die globalen Werte berücksichtigen, dass der Fuss nach einer abgeschlossenen Standphase nicht wieder zurück auf den Ausgangszustand springt, sondern, wie auch in der Realität, in der nächsten Standphase weiter von dem Ausgangspunkt entfernt aufkommt. Eine lokale Betrachtung lässt sich also mit einem Läufer vergleichen, der sich wie auf einem Laufband immer auf derselben Stelle befindet, eine globale Betrachtung hingegen lässt sich mit einem Läufer vergleichen, der auf einem festen Untergrund vorwärts läuft.
Um eine Berechnung der globalen Werte zu realisieren wird ein System benötigt, das den x-Wert der Fussposition um den Betrag erhöht, der in der vorangegangenen Flugphase zurückgelegt wurde. Dieses ist in Abb. 6 und 7 dargestellt. Zunächst erfolgt in einem ersten Schritt ein Abgleich der aktuellen y-Position der Masse und der berechneten y-Koordinate der Landehöhe. Dieser wird durch die Differenz zwischen $x_y$ und $y_L$ realisiert. Sobald diese Differenz den Wert Null erreicht, die Höhe der Masse also kleiner als die vorgegebene Landehöhe wird, liefert der in fallender Richtung eingestellte „Hit-Crossing“-Block ein Signal an das nächste Subsystem, in dem dann die neue Fussposition berechnet wird. Um gegebenenfalls unebene Untergründe simulieren zu können, wurde die Differenz um den Wert der Bodenhöhe ergänzt. Dieser Wert wird hier als y_Ground ($y_{Grd}$) bezeichnet und erhält zunächst den Wert Null, da hier von einem ebenen Untergrund ausgegangen wird. Im Falle einer Simulation mit unebenem Untergrund, muss die Konstante 0 durch eine Funktion des Bodenprofils ausgetauscht werden.
<imgcaption image6|Simulink-Diagramm des Subsystems Fuß>
 </imgcaption>
</imgcaption>
Das durch das Aufsetzsignal ausgelöste Subsystem „Position des Fußes“ berechnet in einem zweiten Schritt den Vektor der aktuellen globalen Fussposition. Dieses Subsystem ist in Abbildung 4 dargestellt. Die y-Position des Fusses entspricht der Bodenhöhe, daher wird der y-Anteil des Fussvektors durch $y_{Grd}$ gebildet. Die Berechnung der Fußkoordinate in x-Richtung erfolgt auf der Basis der x-Koordinate der Masse, auf die noch der Betrag addiert oder subtrahiert wird, mit dem sich der Fuss vor oder hinter der Masse befindet. Dieser entspricht der in Kapitel 2.2 beschriebenen Landehöhe $x_L$ in x-Richtung
<imgcaption image7|Simulink-Diagramm der Fußpunktberechnung>
 </imgcaption>
</imgcaption>
Um die lokalen Parameter für weitere Berechnungen zur Verfügung zu haben, wird eine Differenz zwischen dem Vektor der aktuellen Fußposition und dem Vektor der aktuellen Masseposition gebildet. Diese sorgt dafür, dass das System um den Betrag, der in der Flugphase zurückgelegt wurde zurückgesetzt wird.
Feder
Nachdem das System die Parameter Geschwindigkeit und Ort auf der Basis der aktuellen Ausprägungen berechnen und aktualisieren kann, wird in den drei folgenden Subsystemen implementiert, wie die Modellteile (Feder, Dämpfer und Aktuator) auf die Beschleunigung der Masse in x- und y-Richtung wirken. Die Einwirkungen der Elemente Feder, Kraftaktuator (parallel) und Dämpfer werden zunächst einzeln berechnet und dann per Addition zusammengefasst, ehe sie die als aktuelle Beschleunigung in x- und y-Richtung zurück in das System gegeben werden.
Auf Basis der berechneten Vektoren der aktuellen Geschwindigkeit und Position der Masse und des Fusses, müssen nun noch die Beschleunigungen berechnet werden, die auf die Punktmasse wirken und die als Eingang für den bereits beschriebenen Integrator benötigt werden. Dies geschieht mit Hilfe einer Kraftberechnung. Hierfür müssen die jeweiligen Kraftanteile der Komponenten des Feder-Masse-Dämpfer-Aktuator-Komplexes berechnet werden. Diese werden nach der folgenden allgemeinen Formel in die jeweiligen Beschleunigungsanteile umgerechnet:
$$F = m * a \Leftrightarrow a=\frac{F}{m}$$
Die Einwirkungen der Elemente Feder, Kraftaktuator (parallel) und Dämpfer werden zunächst einzeln berechnet und dann per Addition zusammengefasst, ehe diese als aktueller Beschleunigungsvektor zurück in das System gegeben werden.
Die erste Komponente, die auf die Beschleunigung der Masse einwirkt ist die Feder. Um deren Einwirkung beschreiben zu können, muss zunächst die Wirkungsdauer ermittelt werden. Die Federkraft wirkt ausschließlich während der Standphase. Der Beginn der Federaktivität ist somit der Beginn einer neuen Standphase (Bodenkontakt des Fußes). Das Ende der Federaktivität wird mit dem Zeitpunkt definiert, an dem die Feder ihre Ausgangslänge ($L_0$) wieder erreicht. Mechanisch bedeutet dies, dass die Feder zunächst gestaucht wird, somit eine Druckkraft erzeugt, und sich dann wieder ausdehnt. Sobald beim Ausdehnen die Ruhelänge $L_0$ erreicht wird, wird der Schritt beendet und der Fuss als vom Boden gelöst betrachtet.
In einem ersten Schritt wird aus den $x$- und $y$-Koordinaten der Masse die aktuelle Länge der Feder berechnet. Die Länge ergibt sich zu $\sqrt{x_x^2 + x_y^2}$. Aus dieser Momentanlänge $L$ der Feder kann in einem zweiten Schritt die Längenänderung (hier: Verkürzung) der Feder berechnet werden. Dies geschieht nach folgender Formel:
$$\Delta{L} = (\frac{L_0}{L}-1) * x_{xy}$$
Gemäß der oben genannten allgemeinen Formel der Kraft muss der Term der Stauchung noch mit dem Quotient der Federsteifigkeit und der Masse (k/m) multipliziert werden, um die Beschleunigung zu erhalten:
$$a = \frac{F}{m} = \frac{k*\Delta{L}}{m} = \frac{k}{m}*\frac{L0}{L-1}*x_{xy}$$
In Abb. 8 ist das Blockschaltbild des Subsystems Feder zu sehen. Durch den nach dem Berechnungsblock eingefügten Bedingungsblock wird sichergestellt, dass nur Beschleunigungswerte über den Ausgang 1 ausgegeben werden, solange die Feder gestaucht ist, die Federkraft also einen positiven Wert besitzt. Dieser Bedingungsblock besagt, dass die Eingangsvariable nur weitergegeben werden soll, solange diese einen Wert größer Null besitzt und wird mit folgender Funktion beschrieben: $F*(F>0)$.
<imgcaption image8|Simulink-Diagramm des Subsystems Feder>
 </imgcaption>
</imgcaption>
Im letzten Schritt muss der im unteren Ast des Blockschaltbildes berechnete Term noch mit dem Positionsvektor verrechnet werden und es ergibt sich der Teil des Beschleunigungsvektors der Feder.
Kraft
Um eine aktiv steuerbare Komponente in den Feder-Masse-Dämpfer-Aktuator-Komplex zu integrieren, wird eine zusätzliche Kraft in das System mit eingebaut, die parallel zur Feder und zum Dämpfer wirken soll. Diese Kraft bleibt auf Grund der Einfachheit zunächst eine Konstante. Sollen im späteren Verlauf über die Zeit veränderliche Kräfte betrachtet werden, so muss die Konstante $F$ durch eine Funktion der Kraft in Abhängigkeit von der Zeit ersetzt werden.
Im Subsystem „Kraft parallel“ wird der parallele Kraftaktuator des Laufmodus, beschrieben im Kapitel „Laufen“,implementiert. Hierbei wird die Krafteinwirkung des Aktuators in das System einberechnet, sodass am Ende die Beschleunigung in x- und y-Richtung als Ergebnis des Subsystems ausgegeben wird.
Als Eingangsparameter werden daher die Masse ($m$), die Kraft ($F$), sowie der aktuelle Winkel ($\alpha$) benötigt. Zur Berechnung der x- und y-Komponenten kommt hier nicht der Landewinkel $\alpha_0$ zum Einsatz, sondern es wird der aktuelle Winkel benötigt, der in einem separaten Subsystem berechnet wird. Der Aktuator wirkt immer in Federrichtung und unterstützt daher, abhängig vom Vorzeichen der Kraft den Ausdehn- bzw. Stauchvorgang. Die Beschleunigungswirkung des Aktuators in x-Richtung ergibt sich demzufolge durch den Zusammenhang:
<imgcaption image9|Simulink-Diagramm des Subsystems Kraft>
 </imgcaption>
$$a_x = -cos(\alpha)*\frac{F}{m}$$
</imgcaption>
$$a_x = -cos(\alpha)*\frac{F}{m}$$
Die Beschleunigungswirkung des Aktuators in y-Richtung ergibt sich analog aus:
$$a_y = sin(\alpha)*\frac{F}{m}$$
Die Implementierung der vorgestellten Formeln ist in Abb. 9 zu sehen. Als Ausgang wird aus dem System der Kraftanteil der Beschleunigung als Vektor mit x- und y-Richtung ausgegeben.
Dämpfer
Analog zur Berechnungen in den Subsystemen Feder und Kraft (parallel) wird auch in diesem Subsystem eine Auswirkung, nämlich die des Dämpfers, auf die Beschleunigung in x- und y-Richtung berechnet.
Zunächst wird, analog zur Feder, eine Möglichkeit benötigt, um zwischen einer Flugphase und einer Standphase zu schalten. Da dieses Problem im Subsystem Feder bereits gelöst wurde und die Feder nur dann aktiv ist, wenn der Fuß den Boden berührt, wird die Federkraft in y-Richtung als Referenzgröße zur Bestimmung der Standphase herangezogen. Hat also die Federkraft einen Wert größer Null, so muss auch der Dämpfer aktiv sein. Diese Bedingung wird im unteren Ast des Blockschaltbildes in Abb. 10 realisiert.
In einem zweiten Berechnungskomplex wird dann noch die Dämpferkraft berechnet. Hierzu werden als Eingangsparameter die aktuelle Geschwindigkeit in x- und y-Richtung ($v_x$ u. $v_y$), der aktuelle Winkel $\alpha$ und die Dämpfungskonstante benötigt. Letztere wird außerhalb des Subsystems bereits durch die Masse ($m$) dividiert und tritt als $\frac{b}{m}$ in das Subsystem ein.
<imgcaption image10|Simulink-Diagramm des Subsystems Dämpfer>
 </imgcaption>
</imgcaption>
Zur Berechnung der Auswirkung des Dämpfers auf die Beschleunigung der Punktmasse in x- und y-Richtung ergeben sich dann folgende Zusammenhänge.
Die Beschleunigungsänderung in x-Richtung entspricht:
$$ v_x * cos(\alpha)*\frac{b}{m}$$
Die Beschleunigungsänderung in y-Richtung entspricht:
$$ v_y * sin(\alpha)*\frac{b}{m}$$
Kräfte/Energien
Nachdem das System die Wirkungen der einzelnen Komponenten auf die Beschleunigung der Punktmasse berechnet und summiert hat, stehen dem Integrator die aktuellen Werte zur Verfügung, die dieser zu den erläuterten Berechnungen benötigt.
In diesem letzten Subsystem werden die auftretenden Kräfte und Energien berechnet. Diese gehen teilweise in die Berechnungen der bereits beschriebenen Subsysteme ein, dienen gleichzeitig aber auch als Beschreibungsgrößen der Simulation.
Insgesamt werden sieben verschiedene Größen in diesem Subsystem eingeführt, deren Berechnungen im Folgenden erläutert werden:
- Federkraft
- Federkraft in x-Richtung
- Federkraft in y-Richtung
- Potentielle Energie der Feder
- Potentielle Energie der Punktmasse
- Kinetische Energie der Punktmasse
- Anstellwinkel
Federkraft
Zur Berechnung der Federkraft wird zunächst die Veränderung der Federlänge ($L$) zur Ausgangslänge ($L_0$) berechnet. Hierzu wird die aktuelle Länge der Feder auf der Basis des aktuellen Ortswertes ($x_{xy}$) berechnet. Sie ergibt sich nach Pythagoras zu:
$L = \sqrt{x^2 + y^2}$
<imgcaption image11|Berechnung der aktuellen Federlänge nach Pythagoras>
 </imgcaption>
</imgcaption>
Der Unterschied zur Ausgangslänge ($L_0$) ergibt sich demnach aus dem Zusammenhang:
$\Delta{L} = L_0 - \sqrt{x^2 + y^2}$
Nun kann die Kraft der Feder berechnet werden durch die Formel:
$F_{Feder}=k*\Delta{L}$
Federkraft in x_Richtung
Aus der berechneten Federkraft soll nun der Anteil in x-Richtung extrahiert werden. Dies geschieht durch die Winkelfunktion Kosinus des Anstellwinkels $\alpha$.
$F_x = F * cos(\alpha*\frac{\pi}{180})$
Federkraft in y_Richtung
In gleicher Weise wird der y-Anteil der Federkraft berechnet. Nun wird die Winkelfunktion Sinus des Winkels $\alpha$ verwendet
$F_y = F * sin(\alpha*\frac{\pi}{180})$
Potentielle Energie der Feder
Die Berechnung der potentiellen Energie der Feder ergibt sich aus der Formel:
$E_{Kin} = \frac12 * k * x^2$
Die Federkonstante ($k$) ist als Eingangsparameter in den Anfangsbedingungen festgehalten, die Auslenkung der Feder ($x$) ist aus den Berechnungen der Federkraft bekannt.
Potentielle Energie der Punktmasse
Die Berechnung der potentiellen Energie der Punktmasse ergibt sich aus der Formel:
$E_{Pot}=m*g*h$
Die benötigten Größen $m$, $g$ und $h$ stehen dem Subsystem als Eingangsparameter zur Verfügung, wobei zu beachten ist, dass als Höhe $h$ lediglich die y-Koordinate der Position der Masse in die Berechnung eingeht.
Kinetische Energie der Punktmasse
Die Berechnung der kinetischen Energie der Punktmasse ergibt sich aus der Formel:
$E_{Kin}=\frac12*m*v^2=\frac12*m*\sqrt{v_x^2+v_y^2}^2=\frac12*m*(v_x^2+v_y^2)$
Die benötigten Größen $m$ und $v$ ($v_x$ & $v_y$) stehen dem Subsystem als Eingangsparameter zur Verfügung.
Anstellwinkel
Der Winkel alpha ist nicht in den Anfansgbedinungen festgehalten und muss erst berechnet werden. Dies geschieht auf Grundlage des Zusammenhangs:
$tan(\alpha)=\frac{Gegenkathete}{Ankathete} \Leftrightarrow \alpha = \arctan(\frac{Gegenkathete}{Ankathete})$
Mit den Bezeichnungen aus Abb. 11 ergibt sich Alpha also zu:
$\alpha=arctan(\frac{y}{x})$
Die aufgeführten Berechnungen sind als Blockschaltbild in Abbildung 12 dargestellt:
<imgcaption image12|Simulink-Diagramm der Kräfte- und Energieberechnung>
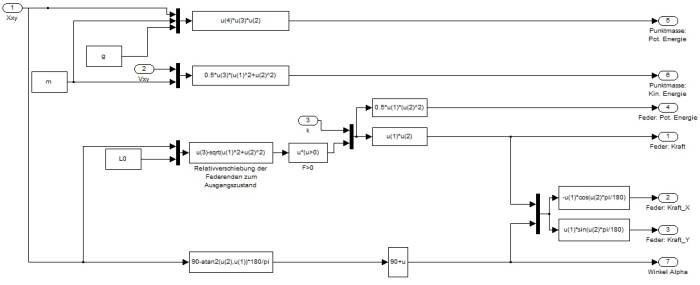 </imgcaption>
</imgcaption>
Literatur
Seyfarth, A. & Rinderknecht, S. (2012). Kick-Off Laufrobotik. Präsentationsfolien im Rahmen des ADP Laufrobotik. Darmstadt: Institut für Sportwissenschaft.
