Inhaltsverzeichnis
WP1205 Radfahren
Einleitung
Das Fahrrad ist ein Fortbewegungsmittel und viele benutzen es im alltäglichen Leben, um von A nach B zu kommen. Es kann aber auch eine Freizeitbeschäftigung sein oder zum Erhalt der Gesundheit dienen. Viele nutzen es für den sportlichen Wettkampf und ein kleiner Teil verdient sein Geld damit. Doch die meisten verfolgen ein Ziel, sie wollen sich möglichst effizient und ökonomisch bewegen.
In unserem Wiki-Projekt betrachten wir das Radfahren aus biomechanischer Sicht und stellen verschiedene Teilaspekte des Radfahrens kritisch vor, insbesondere befassen wir uns mit dem runden Tritt und „Wie“ perfekt diese Technik ist.
Ausgewählte biomechanische Aspekte der Sportart (Daniel Schweizer)
Antriebskraft und Widerstände
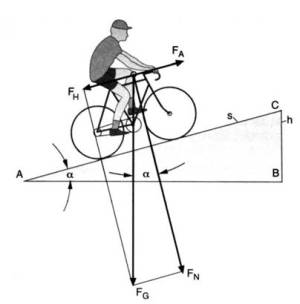
Um einen Gegenstand in Bewegung zu versetzen, sind Kräfte notwendig. Diese Kräfte sind beim Radfahren meistens die Pedalkräfte des Radfahrers, die Schwerkraft beim Gefälle, die Windkraft und die Trägheitskraft beim Ausrollen. Diese Kräfte sollen helfen die Fahrwiderstände zu überwinden. Bei der Vorwärtsbewegung spielen zwei Kräfte eine entscheidende Rolle. Zum einen die Gesamtwiderstandskraft Fges. Sie versucht das Fahrrad mit dem Fahrer zurückzuhalten. Und zum anderen die Antriebskraft FA. Diese Kraft wirkt in Fahrtrichtung. Hierbei wird zwischen drei Fällen unterschieden:
1. FA = Fges :
Um eine konstante Fahrtgeschwindigkeit zu erhalten muss die Antriebskraft genauso groß sein wie die Summe aller Widerstandskräfte.
2. FA > Fges :
Sobald die Antriebskraft größer als die Gesamtwiderstandskraft ist, wird das System beschleunigt.
3. FA < Fges :
Sobald die Gesamtwiderstandskraft größer als die Antriebskraft ist, wird das System gebremst.
 — Abb.1 Gesamtwiderstand und Antriebskraft
— Abb.1 Gesamtwiderstand und Antriebskraft
Trägheitskraft – Beschleunigungswiderstand
Wenn ein Körper bewegt werden soll, muss der Beschleunigungswiderstand zuerst überwunden werden. Sobald dieser überwunden wurde, wird wesentlich weniger der Antriebskraft benötigt, um den Körper in Bewegung zu halten.
Beim weiteren Beschleunigen muss die Trägheitskraft erneut überwunden werden. Dies gilt ebenso für das Bremsen und bei jeder Richtungsänderung.
Der Radfahrer merkt die Trägheitskräfte beim Anfahren, beim Beschleunigen, beim Abbremsen und in Kurven. Die Trägheitskraft hängt von der Masse m sowie der Beschleunigung ab. Dabei verhalten sich die Masse und die Beschleunigung proportional zur Kraft. Daraus erfolgt das „Grundgesetz der Dynamik“ (kraftstoss)
Die resultierende Einheit heißt Newton. Hierbei handelt es sich um die translatorische Trägheitskraft. Neben ihr gibt es auch noch den rotatorischen Beschleunigungswiderstand. Hier werden das Massenträgheitsmoment und die Winkelbeschleunigung benötigt, um das Drehmoment zu erhalten. Wie beim translatorischen Beschleunigungswiderstand sind auch hier Massenträgheitsmoment und Winkelbeschleunigung proportional zum Drehmoment(DYN4 Rotation).
Die rotierenden Teile des Fahrrads tragen nur einen Anteil von etwa 4% zum Trägheitswiderstand bei.
Steigungswiderstand
Der hier zu überwindende Widerstand ist der Steigungswiderstand oder die (Hangabtriebskraft) FH. Die Hangabtriebskraft wirkt bei einer Steigung parallel zur Fahrbahn und versucht das System rückwärts rollen zu lassen. Sie ist ein Teil der Gewichtskraft FG und ist abhängig vom Steigungswinkel α und der Masse des Gesamtsystems m.
Die Arbeit die dabei aufgebracht wird, ist die sogenannte Hubarbeit WH. Sie ergibt sich aus der Gewichtskraft des Systems FG und der Höhe h. Beim Fahren am Gefälle gilt die „Goldene Regel der Mechanik: Was man an Kraft sparen kann, muss man an Weg zugeben„. Das bedeutet, wenn man denselben Höhenunterschied bei einem flacheren Gefälle überwinden will, muss man einen längere Strecke zurücklegen, um dieses Ziel zu erreichen. In beiden Fällen wird jedoch dieselbe Arbeit erbracht.
Je größer die Masse des Systems ist, desto mehr (Hubarbeit) muss verrichtet werden. Jedoch lohnt es sich kaum das Gewicht des Fahrrads zu verringern, wenn der Fahrer selbst übergewichtig ist. Um beim Bergfahren Kraft zu sparen, kann man „Schlangenlinien“ fahren. Sie verringern den Steigungswinkel und somit auch den Steigungswiderstand. Durch Schalten auf eine kleinere Übersetzung kann auch Kraft gespart werden.
Luftwiderstand
Der (Luftwiderstand) FList ist von allen Widerstandskräften die unangenehmste für den Radfahrer. Selbst bei völliger Windstille gehen etwa 80% der Antriebsleistung beim Fahren auf ebener Straße durch den Luftwiderstand verloren. Wenn die Windkraft von der Front oder der Seite kommt, werden die Kräfte addiert. Nur wenn sie von hinten kommt und größer als die Antriebskraft des Fahrers ist, spürt man keinen Luftwiderstand. Deshalb versucht man den Luftwiderstand möglichst gering zu halten. Dies erreicht man durch die Sitzposition. Je weniger Stirnfläche der Windkraft ausgesetzt wird, desto kleiner wird der Luftwiderstand. Auch durch aerodynamische Verkleidungen wird der Luftwiderstand verringert. Eine weitere Möglichkeit um den Luftwiderstand möglichst gering zu halten, ist das Fahren im Windschatten eines anderen Fahrers. Der Luftwiderstand ergibt sich aus dem Strömungswiderstand und den deutlich kleineren Reibungs- und induzierten Widerständen. Da der Strömungswiderstand den Hauptteil der wirkenden Widerstände darstellt, wird auf diesen im Folgenden besonders eingegangen. Der Strömungswiderstand entsteht durch kleine Luftmoleküle, die auf Oberflächen, beispielsweise des Fahrers, treffen und wieder abprallen. Durch das Abprallen entsteht eine Kraft, die senkrecht zur Oberfläche wirkt. Hinter dem Radfahrer bilden sich Wirbelfelder. Dabei wird ein Teil der Bewegungsenergie verbraucht und der Druck sinkt. Der Druck in p2 ist kleiner als in p1 und so für den Strömungswiderstand verantwortlich. Der Strömungswiderstand ist außerdem abhängig von der Luftdichte p, der Stirnfläche A , der quadratischen Anströmgeschwindigkeit v^2 und dem Strömungswiderstandskoeffizienten, dem cW-Wert des Fahrrads. Der Strömungswiderstand ist gleich der kinetischen Energie der Luftmasse.
Die Haltung des Radfahrers und der cW-Wert des Rades spielen also eine Rolle für den Luftwiderstand. Durch eine gebücktere Haltung wird die Stirnfläche des Systems verkleinert. Der cW-Wert ist auch abhängig vom verwendeten Radtyp.
Rollwiderstand
Der (Rollwiderstand) ergibt sich aus dem Walk- und dem Abrollwiderstand. Beim Rollwiderstand gilt das physikalische Grundgesetz actio – reactio. Die Gewichtskraft wird über die Räder auf die Fahrbahn übertragen. Diese Kraft wird durch den Druck in den Reifen ausgeglichen. Beim Rollwiderstand bedeuten 10% geringere Rollreibung einen um 10% längeren Bremsweg. Deshalb ist es wichtig den optimalen Druck zu finden.
Der Walkwiderstand entsteht durch die Verformung der Reifen. Durch die Verformung wird Wärme erzeugt und es entsteht ein bremsendes Drehmoment. Je größer der Reifendruck, desto kleiner ist die Verformung und desto geringer ist der Walkwiderstand. Dabei spielt es keine Rolle ob der Reifen breit oder schmal ist.
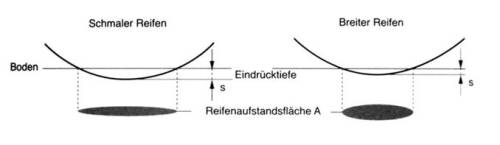 — Abb.4 Rollwiderstand
— Abb.4 Rollwiderstand
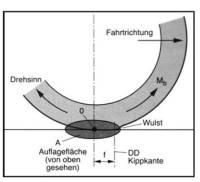
Der Abrollende Reifen schiebt nun einen Wulst vor sich her. Dabei verschiebt sich der Berührungspunkt von Reifen und Fahrbahn nach vorn. Das Rad muss jetzt ständig um die nach vorn gelagerte Kippkante abrollen. Die Folge daraus ist ein bremsendes Drehmoment.
Der Abrollwiderstand setzt sich zusammen aus der Gewichtskraft FG, dem Bodenwert iR und der Abrollwiderstandszahl kR. Je größer der Reifendruck, desto kleiner ist die Verformung und desto kleiner ist auch der Abrollwiderstand, weil die Auflagefläche des Reifens dadurch verkleinert wird. Erhöht man die Masse des Gesamtsystems, wird zwar die Gesamtmasse größer, aber die Abrollwiderstandszahl wird kleiner. Der Anteil des Abrollwiderstandes am Rollwiderstand beträgt ungefähr 90%. Dabei spielen verschiedene Bodenarten auch unterschiedliche Rollen.
Reibungswiderstand der schwingenden Teile
Bei gleichbleibender Geschwindigkeit auf horizontaler Fahrbahn treten neben dem Luft- und dem Rollwiderstand noch der Reibungswiderstand der schwingenden Teile, durch mechanische Reibung in den Lagern und der Kette auf. Der Wirkungsgrad einer sauberen Kette liegt bei ca 0,98. Mit den anderen Reibungspunkten sollte ein Wirkungsgrad von η = 0,96 entstehen. Das bedeutet, dass etwa 4% der Antriebsleistung, die den Rollwiderstand überwindet, durch die mechanische Reibung verloren geht. Untersuchungen haben ergeben, dass der Verlustprozentsatz bei kleineren Geschwindigkeiten etwas geringer ist als bei größeren.
Schwingungswiderstand
Durch Leistungsverlust kann es beim Radfahren auch noch durch Schwingungen kommen. Diese Schwingungen entstehen durch den Tritt in die Pedale, die Veränderung der Lage des Fahrers, Unebenheiten in der Farhbahn, Unwucht in den Rädern und Spiel in den Lagern und im Lenkkopf. Jede Kraft die auf das Fahrrad einwirkt führt zu einer elastischen Verformung der belasteten Teile. Dieser Arbeitsverlust kann auch als Dämpfung angesehen werden.Steife Konstruktionen haben im Vergleich zu weichen Materialien einen geringeren Arbeitsverlust. Je höher die Geschwindigkeit ist, desto höher ist auch die Dämpfung. Die Schwingungen können auch zu einem Rahmenflattern führen. Im Extremfall führt diese Resonanz zu Stürzen. Um dem entgegenzuwirken, sollten die Einzeleile des Rades möglichst unterschiedliche Eigenfrequenzen besitzen. Durch eine größere Dämpfung entsteht zwar ein Verlust an Arbeit, jedoch ist es schonender für Mensch und Material.
Muskulatur-Einsatz beim Radfahren (Sean Donnelly)
Zur Veranschaulichung der zyklisch-dynamischen Bewegung des Radfahren und der dabei benutzten Muskulatur im Oberschenkel unterteilen wir den Trittvorgang in vier Bereiche:
1. Schubphase
2. Druckphase
3. Zugphase
4. Hubphase
Bei der Betrachtung der Muskulatur des Unterschenkels und der Fußmuskulatur unterteilen wir den Bewegungsablauf in:
A. Heben
B. Senken
1. Schubphase
Wie der Name dieser Phase bereits andeutet, wird in diesem Teilabschnitt das Pedal idealerweise aktiv nach „vorn“ (in Fahrtrichtung) geschoben. Hierbei verrichten die Extensoren,des Oberschenkels, also der vierköpfige Oberschenkelmuskel (musculus quadriceps fermoris), die Hauptarbeit. Die vier Teilmuskeln, der gerade Schenkelmuskel (rectus femoris, rf), der äußere Schenkelmuskel (vastus lateralis, vl), der mittlere Schenkelmuskel (vastus intermedius, vi) und der innere Schenkelmuskel (vastus medialis, vm), setzten alle gemeinsam über die Patellasehne (in der die Kniescheibe sitzt) am Schienbein an, wodurch sie eine Streckung des Kniegelenks bewirken. Mittels dieser Steckung wird das Pedal nach vorne geschoben.
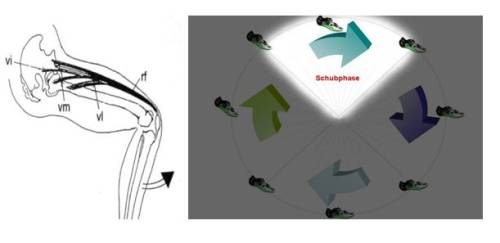 — Abb.7 Schubphase
— Abb.7 Schubphase
2. Druckphase
Für das nach „unten„ Drücken des Pedals ist der große Gesäßmuskel (musculus gluteus maximus) (siehe Bild: gm) verantwortlich.
Eine seiner Sehnen setzt am Unterschenkel an, womit er auch für dessen Streckung mitverantwortlich ist und somit das gesamte Bein nach „unten“ drückt. Der Quadtrizeps unterstützt und stabilisiert diese Bewegung jedoch zusätzlich.
Durch die nach vorn gebeugte Haltung des Oberkörpers auf dem Rad dehnt man den Gesäßmuskel über seine Ruhelage hinaus und bewirkt somit eine Vorinnervation/Vorspannung des Muskels, was eine noch höhere Kraftentwickelung bewirkt, da der Muskel „zurückfedert„.
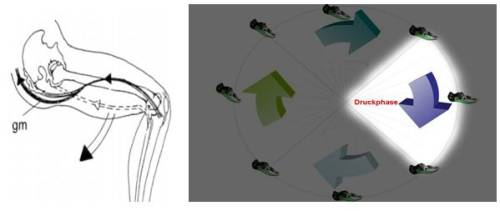 — Abb.8 Druckphase
— Abb.8 Druckphase
3. Zugphase
Das Beugen des Unterschenkels übernimmt die ischiocrurale Muskelgruppe auf der Rückseite des Oberschenkels, bestehend aus dem musculus semimembranosus (sb), dem musculus semitendinosus (st) und dem musculus biceps femoris (bf). Im Englischen ist diese Muskelgruppe besser bekannt unter „Hamstrings“.
 — Abb.9 Zugphase
— Abb.9 Zugphase
4. Hubphase
Beim nach „oben“ Ziehen des Beines verrichtet den größten Anteil an der Bewegung der gerade Oberschenkelmuskel, musculus rectus femoris (rf), welcher auf Grund seines oberen Ansatzes oberhalb der Hüfte, sowohl das Bein heben als auch - wie oben beschrieben - strecken kann.
Zusätzlich hebt der kräftigste Hüftbeuger, der Lendenarmbeinmuskel musculus iliopsoas, den Oberschenkel. Er besteht aus dem Lendenmuskel musculus psoas (p) und dem Darmbeinmuskel musculus iliacus (i).
 — Abb.10 Hubphase
— Abb.10 Hubphase
Unterschenkelmuskulatur, Fußmuskulatur
A.Senken
Beim Absenken des Fußes arbeiten und stabilisieren beide WadenMuskeln, der Zwillingswadenmuskel musculus gastrocnemius (ga) und der Schollenmuskel musculus soleus (so), die Bewegung mit. Beide setzen über die Achillessehne(a) am Fuß an.
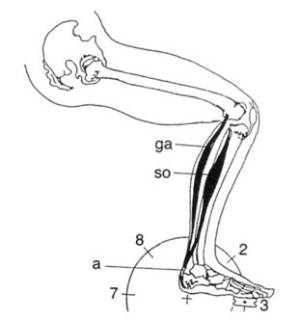 — Abb.11 Muskulatureinsatz beim Senken
— Abb.11 Muskulatureinsatz beim Senken
B.Heben
Die Hebebewegung des Fußes bewirken drei Muskeln, der vordere Schienbeinmuskel musculus tibialis anterior (ta), der lange Großzehenstrecker musculus extensor hallucis longus (hl) und der Zehenstrecker musculus extensor digitorium longus (dl).
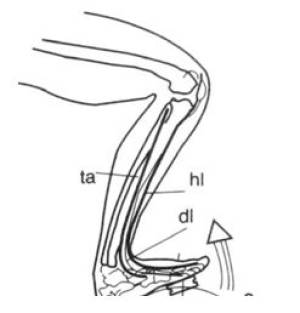 — Abb.12 Muskulatureinsatz beim Heben
— Abb.12 Muskulatureinsatz beim Heben
Der runde Tritt (Paul Schuster)
Als runden Tritt bezeichnet man die Fähigkeit, die Kraft während der gesamten Pedalumdrehung gleichmäßig von den Füßen auf die Pedale zu übertragen und das möglichst während der ganzen 360° der Pedalumdrehung.
Biomechanische Grundlagen
Eine Pedalumdrehung wird durch eine Kreisbahn beschrieben. Es treten also verschiedene Winkel auf. Eine Pedalumdrehung beschreibt einen Winkel von 360°. Steht der Kurbelarm senkrecht nach oben, so markiert dieser den Punkt 0° beziehungsweise 360°. Zeigt der Kurbelarm senkrecht nach unten so beträgt der Winkel 180°, diese beiden Positionen werden auch als Totpunkt bezeichnet.
Wirkende Kräfte
In der folgenden Abbildung soll veranschaulicht werden welche Kräfte während einer Pedalumdrehung auftreten.
Bei einer Pedalumdrehung werden verschiedene Kräfte vom Fuß über das Pedal auf die Kurbel übertragen. Hierbei muss man zwischen drei Kräfte unterscheiden: der Radialkraft, der Tangentialkraft und der daraus resultierenden Gesamtkraft.
Radialkraft: Erzeugt kein Vortrieb, wirkt entlang der Kurbel als Stauchung oder Längung, sollte gering gehalten werden.
Tangentialkraft: Vortriebsbringende Kraft, greift immer rechtwinklig zur Kurbel an, ist die gewünschte Kraft.
Resultierende Kraft: greift an der Kurbel an, setzt sich aus der Radialkraft und der Tangentialkraft zusammen. (Kräfteparallelogramm http://de.wikipedia.org/wiki/Kr%C3%A4fteparallelogramm)
Aus biomechanischer Sicht kann man erst dann von einem „runden Tritt“ sprechen, wenn die resultierende Kraft zu jedem Zeitpunkt gleich der vortriebswirksamen Tangentialkraft ist und somit das Drehmoment zu jeder Pedalstellung gleich groß ist.
Drehmoment
Trifft die Gleichheit des (Drehmoments) zu, so hat dies physikalisch gesehen zwei Vorteile. Während der gleichmäßigen Kräfteverteilung auf das Pedal muss keine Beschleunigungsarbeit geleistet werden und das System besitzt einen gleichmäßigen Antrieb. Beide Punkte unterstützen das effiziente und ökonomische Fahren.
Voraussetzung für die Anwendung dieser Antriebsart ist eine feste Verbindung zwischen dem Schuh und dem Pedal. Meistens wird diese Verbindung mit einem Klickpedalsystem hergestellt, hierbei ist unter dem Schuh eine Platte befestigt, die in das Pedal „eingeklickt“ wird.
Bewegungsstruktur des runden Tritts
Um die Bewegung des runden Tritts besser verstehen zu können teilt man die Trittbewegung am besten in vier Phasen oder Sektoren ein.
Man unterscheidet zwischen der Schub-Phase, der Druck-Phase, der Zug-Phase und der Hub-Phase.
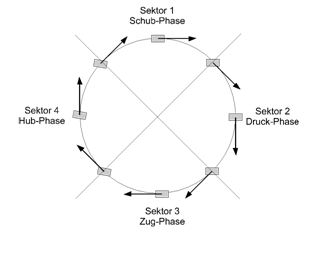
— Abb.15 Sektoren des Kurbelwegs
Sektor 1
Schub-Phase 316° bis 45°: Dieser Sektor beschreibt den Übergang von der Zug-Phase in die Druck-Phase. Um den runden Tritt möglichst effektiv zu gestalten, sollte man in dieser Phase den Fuß aktiv nach vorne schieben, mit dem Ziel, den oberen Totpunkt möglichst ökonomisch und schwungvoll zu überwinden.
Sektor 2
Druck-Phase 46° - 135°: Im Sektor der Druck-Phase erreicht der Radfahrer sein Kraftmaximum. Zwischen einem Winkel von 90° und 110° wird der größte Vortrieb erzeugt und somit das physikalische Optimum erreicht. Bedingt durch die Sitzposition und der Stellung des Kurbelarms ist es möglich in diesem Bereich die höchste vortriebswirksame Tangentialkraft zu erzielen.
Sektor 3
Zug-Phase 136° - 225°: Trotz andauernder Druck-Phase setzt die Zug-Phase ein. Hierbei wird der Fuß aktiv nach hinten gezogen und gleichzeitig wird das Bein gestreckt. Das aktive nach hinten Ziehen des Fußes ermöglicht diesmal das ökonomische Überwinden des unteren Totpunktes.
Sektor 4
Hub-Phase 226° - 315°: Dieser Bereich markiert den entscheidenden Sektor für den runden Tritt. Der Fahrer versucht das Pedal aktiv nach oben zu ziehen und somit weiterhin vortriebswirksame Kräfte zu erzeugen.
Kritische Würdigung des runden Tritts (Nicolas Bayer)
Beide Videos zeigen den Tritt eines Triathleten. Versuche mit Hilfe der Definition des runden Tritts und der biomechanischen Erläuterungen die Technik zu bewerten.
Sicherlich erwies sich eine genaue Zuordnung anhand der Kriterien des runden Tritts als äußerst komplex. Die Problematik der Quantifizierung des runden Tritts führte zu einer Unterrepräsentation in der Trainingslehre, da eine rein visuelle Analyse nur selten mit der gemessenen (mechanischen Effizienz)übereinstimmt. Dies belegt eine Studie von Suhr (1992).
Im Rahmen dieser Untersuchung sollten 24 Radsporttrainer die Trettechnik von 10 Radsportlern unterschiedlicher Leistungsklassen mit Hilfe von Videoaufzeichnungen beurteilen. Es zeigte sich, dass die Bewegungsgeschwindigkeit als vorangiges Kriterium zur Beurteilung der Technik genutzt wurde. Die Einschätzungen der Trainer stimmten nicht mit den empirisch ermittelten Werten überein. Ein visuell erkennbares Technikleitbild scheint folglich nicht zu existieren. Weitere Studien konnten darüber hinaus Abweichungen zwischen intrinsicher Rückmeldungen der Sportler und den gemessenen Werten nachweisen (Hoes et al. 1968, Cavanagh und Sanderson 1986).
Sanderson setzte in diesem Zusammenhang das Real-Time Feedback System (1987) ein, um die Problematik der mangelnden Rückkopplung zu beheben. So konnte unter anderem Henke (1994) einen postiven Trainingseffekt durch biomechanische Rückmeldungen feststellen.
Neben der geschilderten Diskrepanz zwischen der visuellen Analyse beziehungsweise der intrinsichen Rückkopplung und den Empirischen Befunden steht der runde Tritt auch wegen seinem fehlenden Bezug zur Praxis in der Kritik. Untersuchungen der Tretttechnik von Spitzenradsportlern von Hillebrecht et al. (1998) zeigten, dass es sogar in dieser Zielgruppe zu Abweichungen bezüglich der Idealvorstellung des runden Tritts kommt.
Besonders in der Hub-Phase (Sektor 4) weicht der Wert von den optimalen Wirkungsgraden (100) sehr stark ab. Lediglich ein Fahrer konnte eine vortriebswirksame Kraft erzeugen (Fahrer C). Alle anderen Fahrer erzeugten Kräfte entgegen der Drehrichtung. In Sektor 3 und 4 ruht das Bein meistens passiv auf der Kurbel. Es erfolgt oft aus Gründen der Ökonomie oder der Koordination kein aktives Heben oder Ziehen.Dies führt zu den nur geringen oder negativen Wirkungsgraden in diesen Sektoren. Das fokusierte Trainieren der Zug- und Hub-Phase geht meist mit einem Verlust in der Schub-Phase einher. Da in dieser Phase jedoch die bestmöglichen Winkelverhältnisse herrschen sollte dies vermieden werden.
Neben diesen allgemeinen Abweichungen zum Technikleitbild verweist Hillebrecht insbesondere auf die interindiviuellen Unterschiede der Fahrer (siehe Tabelle), obwohl es sich bei allen um nationale Spitzenatheten handelt.
Es scheint demnach kein allgemeines Technikleitbild wie etwa den runden Tritt zu existieren. Selbst Spitzenathleten erreichen mit einer individuellen Verteilung der Wirkungsgrade in den einzelnen Sektoren eine vergleichbare Leistungsfähigkeit.
Konditionelle Aspekte bestimmen die physiologische Leistungsfähigkeit weit mehr als die mechanische Effizienz. Die Kraftverteilung wird über einen Kurbelzyklus individuell realisiert. Da der Mensch durch seinen Körperbau nicht in alle Richtungen gleich gut Kräfte aufbringen kann, zeigt sich die Kraftentfaltung abhängig von Gelenkwinkeln und der Bewegungsgeschwindigkeit der beteiligten Muskeln (Böhm,Cole,Brüggemann & Ruder, 2006). Diese physiologischen Einflussgrößen werden im Kriterium der mechnischen Effizienz, welches sich stark an der Definition des runden Tritts orientiert, nicht berücksichtigt. Aus diesen Gründen wird ein Kriterium zur Bewertung der Trettechnik, dass die biomechanischen Eigenschaften des menschlichen Körpers einbezieht, angestrebt.
In Zusammenarbeit mit dem Radlabor Frankfurt führten wir eine Pedalkraftanalyse durch um die geschilderte Problematik im Zusammenhange des „Runden Tritts“ zu reproduzieren.
 — Abb.16 Vortriebswirksame Kräfte
— Abb.16 Vortriebswirksame Kräfte
Die Linke Graphik zeigt die gemessenen vortriebswirksamen Kräfte (Linkes Bein – rot, Rechtes Bein- grün) im Vergleich zu einer Null-Linie (schwarz). Auch bei den von uns gewonnen Daten ist zu erkennen das die größte Kraft in Sektor 2 erbracht wird. In Sektor 4 wurden keine vortriebswirksamen Kräfte erbracht. Auch der Kraft-Kurbelwinkelverlauf verdeutlicht dies.
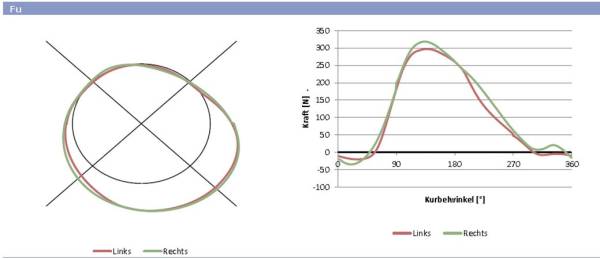 — Abb.17 Nichtvortriebswirksame Kräfte
— Abb.17 Nichtvortriebswirksame Kräfte
Neben den Tangentialkräften werden auch die Radialkräfte zur Analyse herangezogen. Wir konnten mit unserer Messung ebenfalls die Ergebnisse von Hillebrecht bestätigen. In Sektor 3 und 4 nimmt der Anteil der Radialkräfte an der resultierenden Kraft zu. In Sektor 1 und 2 überwiegt der Anteil der Vortriebswirksamen Kräfte (Tangentialkräfte).
Des Weiteren könnte aus beiden Graphiken eine eventuelle muskuläre Disbalance abgelesen werden. Je größer die Abweichungen zwischen Roter und Grüner Kurve, desto ausgeprägter liegt ein Missverhältnis zwischen rechtem und linkem Bein vor.
Fragen zur Wiederholung
- Welche Folgen hat es, wenn der Luftdruck des Reifens verändert wird ?
- In wieviele Phasen kann eine Kurbelumdrehung unterteilt werden? Benenne diese!
- Lässt sich der runde Tritt in die Praxis übertragen?
Literatur
- Fahrradphysik und Biomechanik, Michael Gressmann, 2009, Bielefeld
- Bicycling Science, Frank Rowland Whitt & David Gordon Wilson,1993,Massachusetts
- 23.Internationales Triathlon-Symposium,Martin Engelhardt,Birgit Franz, Georg Neumann & Arndt Pfützner, 2008, Erding
- Konopka, P. (2000), Radsport. München: BLV Verlagsgesellschaft mbH
- Hillebrecht, M., Schwirtz, A., Stapelfeld, B. (1998). Tritttechnik im Radsport. Der „runde Tritt“ – Mythos oder Realität
Abbildungsverzeichnis
- Abbildung 1: Fahrradphysik und Biomechanik, Michael Gressmann, 2009, Bielefeld, S. 26
- Abbildung 2: Nach Fahrradphysik und Biomechanik, Michael Gressmann, 2009, Bielefeld, S. 41
- Abbildung 3: Fahrradphysik und Biomechanik, Michael Gressmann, 2009, Bielefeld, S. 69
- Abbildung 4: Fahrradphysik und Biomechanik, Michael Gressmann, 2009, Bielefeld, S. 51
- Abbildung 5: Fahrradphysik und Biomechanik, Michael Gressmann, 2009, Bielefeld, S. 52
- Abbildung 7:Fahrradphysik und Biomechanik, Michael Gressmann, 2009, Bielefeld
- Abbildung 8:Fahrradphysik und Biomechanik, Michael Gressmann, 2009, Bielefeld
- Abbildung 9:Fahrradphysik und Biomechanik, Michael Gressmann, 2009, Bielefeld
- Abbildung 10:Fahrradphysik und Biomechanik, Michael Gressmann, 2009, Bielefeld
- Abbildung 11:Fahrradphysik und Biomechanik, Michael Gressmann, 2009, Bielefeld
- Abbildung 12:Fahrradphysik und Biomechanik, Michael Gressmann, 2009, Bielefeld
- Abbildung 13:Hillebrecht, M., Schwirtz, A., Stapelfeld, B. (1998). Tritttechnik im Radsport. Der „runde Tritt“ – Mythos oder Realität
- Abbildung 15:Hillebrecht, M., Schwirtz, A., Stapelfeld, B. (1998). Tritttechnik im Radsport. Der „runde Tritt“ – Mythos oder Realität
Bewertung des Wiki-Moduls
| Kategorie | Bayer | Donnelly | Schuster | Schweizer | Anmerkungen |
|---|---|---|---|---|---|
| Inhalt (max. 10) | 8 Pkt | 8 Pkt | 6 Pkt | 8 Pkt | Drehmoment besser erklären |
| Form (max. 5) | 3 Pkt | 4 Pkt | 4 Pkt | 3 Pkt | |
| Bonus (max. 2) | 1 Pkt | 0 Pkt | 0 Pkt | 0 Pkt | Kritische Würdigung des Runden Tritts |
| Einzelbewertung | 12 Pkt | 12 Pkt | 10 Pkt | 11 Pkt | 15 Punkte = 100% |
| Gesamtbewertung | 45/60 Punkte = 75% |