Inhaltsverzeichnis
KINSCRIPT01
| Modul | Winkelberechnung |
|---|---|
| Kategorie | MATLAB > MAT-KINSCRIPT |
| Autor | Filip Cengic |
| Voraussetzung | Matlab-Grundlagenkenntnisse: MAT01 Einführung optional: MAT02 Baumgartner - MAT04 Grafische Darstellung |
| Bearbeitungsdauer | ca. 30 Minuten |
| Skripdatei | anglecalculation.m |
| Datensatz | P1W25 |
Im Folgenden wird das – oben zum Download angebotene – Matlab-Skript Schritt für Schritt erklärt. Das Skript bezieht sich auf den zur Verfügung gestellten Datensatz. Der Datensatz beinhaltet die jeweiligen Markerpositionen (nx3 Matrizen), sowie de gemessenen Bodenreaktionskräfte.
…zum Datensatz:
- Der Datensatz kann hier heruntergeladen werden. Dort findet sich auch eine nähere Beschreibung dieses.
- Die Kodierung der Marker ist in Markercodes (Links) beschrieben.
…zum Skript:
Das Skript benötigt für die Winkelberechnung drei Parameter. Zunächst ist ein Drehpunkt zu definieren (z.B. Kniegelenk). Um das Kniegelenk rotieren sowohl Oberschenkel (Verbindung Hüfte-Knie) als auch Unterschenkel (Verbindung Fuß/Hacke-Knie). Dementsprechend werden folgende drei Marker als Parameter in die Winkelberechnung übergeben(linksseitig):
- L_Hee – Left Heel: Linke Hacke
- L_Hip – Left Hip: Linker Hüftknochen
- L_Kne_O – Outer Left Knee: Äußeres linkes Knie
Das Skript lässt sich in sechs Teile untergliedern, welche im Folgenden näher erläutert werden:
- Bereinigung des Workspace/Kommandozeile
- Parametereingabe
- Relative Koordinaten definieren
- Winkelberechnung
- Darstellung
- Datensicherung (optional)
(1) Bereinigung der Kommandozeile
(2) Parametereingabe
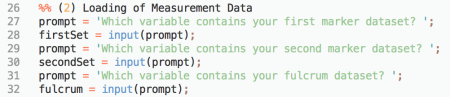
In diesem Abschnitt werden im Dialog zur Skriptlaufzeit die Parameter festgelegt (Drehpunkt, zwei in Verbindung stehende Marker). Die Reihenfolge spielt hierbei keine Rolle, welcher der beiden Verbindungsmarker zuerst gewählt wird. Die Dialogabfrage geschieht mit dem Befehl prompt. Der Befehl input liest die Nutzereingabe ein (Zeilen 28, 30, 32), welche der entsprechenden Skriptvariable zugewiesen wird. Bei der dritten Abfrage ist der Drehpunkt zu definieren.
(3) Relative Koordinaten definieren
Die jeweiligen Markerpositionen werden übersichtshalber in ihre x-, y- und z-Komponente untergliedert (Zeilen 36-45). Des Weiteren wird der eindimensionale Vektor targetAngle initialisiert (Zeile 49), welcher im nächsten Schritt in einer for-Schleife (Zeilen 53-61) mit Winkelwerten befüllt wird.
(4) Winkelberechnung
Die mathematischen Eigenschaften des Skalarprodukts zweier Vektoren geben Information zu dem Winkelverhältnis. Bevor näher auf die Skalarproduktgleichung eingegangen wird, sind zunächst die jeweiligen Vektorlängen zu bestimmen. Hierzu werden die beiden Markerpositionsvektoren voneinander subtrahiert (Zeilen 54, 56). Für die Berechnung der „natürlichen“ Länge (Euklidisches Länge) eines Vektors wird die Funktion $norm(X)$ verwendet. Hierbei entspricht $norm(X) = norm(X, 2) = sqrt(sum(X.^2))$, wobei $X.^2$ bedeutet, dass jede einzelne Komponente des Vektors $X$ quadriert wird.
Mathematisch ausgedrückt ist die Euklidische Länge mit p-norm (hier: p=2) wie folgt definiert:
$$ \lVert X \rVert_{p} := \Big( \sum_{i=1}^{n} \vert X_i \vert^p \Big)^{\frac{1}{p}} $$
Exkurs: Verwendung des Skalarprodukts
Das Skalarprodukt beschreibt das Winkelverhältnis zweier Vektoren und kann mit der folgenden Gleichung ausgedrückt werden:
$$ \vec{a} * \vec{b} = \vert \vec{a} \vert \vert \vec{b} \vert cos(\gamma) $$
Die folgende Tabelle führt ein Beispiel auf. Abhängig vom Kniewinkel wird entschieden, ob das Skalarprodukt negativ, positiv oder gleich 0 beträgt:
| Kniewinkel $\gamma$ | Skalarprodukt |
|---|---|
| =90° | $\vec{a}*\vec{b}=0$ |
| <90° | $\vec{a}*\vec{b}>0$ |
| >90° | $\vec{a}*\vec{b}<0$ |
Beträgt der Winkel < 90°, ist das Skalarprodukt positiv und umgekehrt (>90°) negativ. Der Grund ist der Kosinusverlauf, welcher ab einer Winkelgröße von >90° (und <180°) negativ ist. Vektorlängen beschreiben einen Abstand zueinander, daher sind $\vert \vec{a} \vert$ , $\vert \vec{b} \vert$ stets >0.
Über das Skalarprodukt ist es folglich möglich, den Winkel zu berechnen. Durch mathematische Termumformung kann der $cos(\gamma)$ auf die linke Seite der Gleichung gebracht werden (Zeile: 58):
$$ cos(\gamma) = \frac{\vec{a}*\vec{b}}{\vert \vec{a} \vert \vert \vec{b} \vert} $$
Der Kosinus aus dem Kniewinkel entspricht der Division zwischen Skalarprodukt und Multiplikation der „natürlichen“ (auch: euklidischen) Vektorlängen.
In den Zeilen 63-78 werden die in Punkt (3) und (4) erzeugten temporären Vektoren aus dem Workspace gelöscht. Der Kniewinkelverlauf wurde iterativ in der Variable targetAngle (Zeile 60) gespeichert.
(5) Darstellung
Die grafische Darstellung erfolgt mit dem Matlab-Befehl plot(X,Y) in Zeile 83. Als Eingangsparameter Y wird der targetAngle verwendet.
(6) Datenspeicherung
Per Nutzerinteraktion wird gefragt, ob der ausgewertete Datensatz in einer .mat-Datei lokal gespeichert werden soll.
Video
Das Video befindet sich gerade in Bearbeitung und wird demnächst fertiggestellt.
Feedback
Wo gibt es noch offene Fragen? Was sollte besser erklärt werden? Rechtschreibfehler gefunden? Auch allgemeines Feedback, Ideen und Wünsche sind herzlich willkommen!
Das Feedback kann ohne Anmeldung im folgenden Google Dokument festgehalten werden.