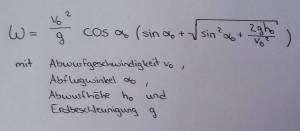Inhaltsverzeichnis
WP1310 Speerwurf
| | WP1310 - Speerwurf |
|---|---|
| Veranstaltung | PS Biomechanik |
| Autor | Laura Gieser, Sebastian Trittenbach, Florian Kunz |
| Bearbeitungsdauer | 60 min |
| Präsentationstermin | 21.01.2014 |
| Zuletzt geändert | 08.04.2014 |
Einleitung
Dieses Wiki beschäftigt sich mit dem Speerwurf und baut auf das Wiki-Projekt Wurf auf, in welchem die Phasenstruktur des Speerwurfs schon behandelt wurde. Unser Hauptaugenmerk liegt jedoch auf der Wurftechnik, die sich hauptsächlich auf die Abwurfphase bezieht, und der Flugmechanik. Bevor wir darauf genauer eingehen möchten, wollen wir euch zuerst einen Überblick über die Geschichte des Speerwurfs und die Veränderung des Materials geben. Wir starten mit einem Video von Matthias de Zordo, bei dem sowohl der Abwurf wie auch die Flugphase des Speers gut zu sehen sind.
Einführendes Beispiel
Historie und Material
Geschichte
Der Speer hat sich von der Jagdwaffe, über die Kampfwaffe, bis hin zum Sportgerät entwickelt. In der griechischen Antike wurde das Speerwerfen erstmals als Wettkampf eingeführt und war fester Bestandteil der Olympischen Spiele der Antike. Bis er schließlich im Jahre 1906 in die Olympischen Spiele der Neuzeit aufgenommen wurde, hat sich jedoch vieles an dem Material des Speers und der Wurftechnik verändert.
Material
Die ersten Speere, welche als Jagdwaffen eingesetzt wurden, waren den Überlieferungen nach aus Tannen- oder Fichtenholz und besaßen als Spitze einen geschärften Stein.
In der Antike hatte sich der Aufbau verändert. Der Speer war zwar ebenfalls noch aus Holz (meist Birkenholz), besaß aber eine Metallspitze und hatte zusätzlich eine Wurfschlinge (Ankyle). Diese war eine Lederschnur, die kurz hinter dem Schwerpunkt des Speers befestigt war und durch einen verlängerten Armhebel eine bessere Rotationsbewegung ermöglichte.
Erst seit 1920 wich man von der Konstruktion des Speers, der vollkommen aus Holz gebaut wurde, ab und ersetzte diesen durch einen Hohlspeer, welcher zunächst aus geleimtem Holz, später aus (Leicht-)Metallen bestand. Heutzutage sind die meisten Speere aus Metall, Aluminium, Carbon oder Legierungen (Metallgemischen) (Fuchser, I. Kleine Speerkunde).
Vergleich des Schwerpunkts von alten und neuen Speeren
Durch eine ständige Optimierung von Form, Material und Schwerpunkt, verbesserte sich die Flugeigenschaft des Speers stetig und somit auch die maximale Wurfweite. Nachdem Uwe Hohn 1984 einen neuen Weltrekord mit 104,80m aufgestellt hatte, kam es 1986 zu einer Regeländerung der Konstruktion, da die Gefahr enstand, andere Athleten auf der gegenüberliegenden Seite des Leichtathletikstadions mit dem Speer zu treffen. Der Schwerpunkt des Speers wurde 4cm nach vorne verlagert und die Speeroberfläche wurde verkleinert. Dies hatte zu Folge, dass eine kleinere Flugkurve erzielt wurde, da sich die Spitze des Speers somit im letzten Drittel des Flugs früher nach unten senkt.
Der neue Weltrekord liegt momentan bei den Männern bei 98,48 m, erzielt von dem tschechischen Athleten Jan Železný 1996, und bei den Frauen bei 72,28 m, ebenfalls von einer tschechischen Athletin Barbora Špotáková 2008.
In den folgenden Grafiken kann man das Flugverhalten des Speers mit dem alten und dem neuen Schwerpunkt vergleichen. Es wird deutlich, dass sich die Flugkurven im letzten Drittel stark unterscheiden. Während der alte Speer länger schief in der Luft stehen bleibt, bevor er nach vorne abkippt und fast waagerecht auf dem Boden landet, fällt die Speerspitze des neuen Speers früher nach unten. Somit wird die Flugkurve verkleinert und der Speer hinterlässt zuerst mit der Spitze einen Abruck auf dem Boden, wodurch ungültige Würfe, wie es bei der Flugkurve des alten Speers oft der Fall war, vermindert werden können (Fuchser, I. Kleine Speerkunde).
Wurftechnik
Unsere Technikanalyse baut auf die Weitenformel für den Speerwurf auf. Anhand dieser wollen wir veranschaulichen, welche Wirkung Fehler auf die Wurfweite haben und wie man diese optimieren kann.
Beispiel:
Angenommen der Winkel beträgt nur 40°, die Abwurfgeschwindigkeit 30 m/s, die Abwurfhöhe 1,70m und die Erdbeschleungigung 9,81m/s².
Nach der Weitenformel ergibt sich W=88,57m
Fazit: Die Wurfweite hängt hauptsächlich von der Abwurfgeschwindigkeit und dem Abwurfwinkel ab.
Dies sind auch unsere zwei Unterpunkte, die wir im Weiteren genauer untersuchen wollen.
verfasst von Laura Gieser
Abwurfgeschwindigeit
Die Abwurfgeschwindigkeit setzt sich aus der Anlauf - und der Abwurfbeschleunigung, welche rein durch die Arm- und Handmuskulatur zustande kommt, zusammen.
Nun betrachten wir die Anlaufbeschleunigung.
Wichtige Knotenpunkte sind hierbei nach Killing (2011, S.143):
- Abdruck zum Impulsschritt (für Rechtsshänder: Schritt von links nach rechts)
- Druckbein-Aufsatz
- Stemmbein-Aufsatz
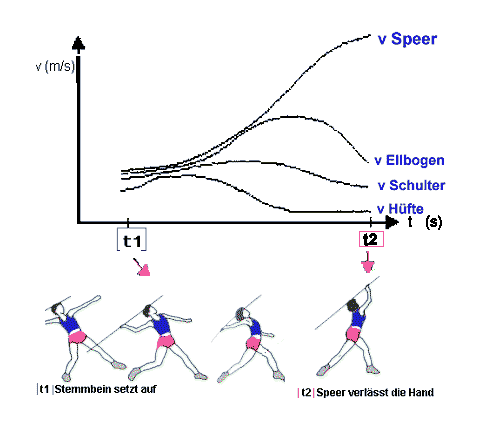
Welche Wirkung der Knotenpunkt Stemmbein-Aufsatz und seine Durchführung auf die Wurfweite haben, zeigen wir nun.
Anhand von Abbildung 4 erkennt man die bedeutende Funktion des Stemmbeins, welche eine große Rolle für die Endgeschwindigkeit des Speers spielt.
Doch nun betrachten wir den Fall, dass dieser Stemmschritt „überlaufen“ wird, beziehungsweise falsch ausgeführt wird, anhand zweier Bilder.
Vergleichen wir nun das linke, falsche, mit dem rechten, richtigen, Bild.
Bei beiden Bildern achten wir nur auf die Beine und stellen fest, dass beim linken Abwurf das linke Stemmbein im Kniegelenk eine Beugung hat, sowie einen Fußaufsatz auf dem Fußballen. Dies sind zwei Indikatoren für einen falschen Einsatz des Stemmbeins.
(Institut für Motorik und Bewegungstechnik, S.24)
Der Speer wird somit nicht durch abruptes Stoppen nach vorn beschleunigt, sondern nurnoch aus dem Arm geworfen, da die Geschwindigkeit aus dem Anlauf „verpufft“.
Zur besseren Vorstellung des Stemmschritts: Ein Auto fährt gegen die Wand und die Insassen werden nach vorn geschleudert. Ähnlich ist die Wirkung des Stemmschritts. Findet jener nicht statt, wird auch der Speer nicht nach vorne geschleudert.
verfasst von Sebastian Trittenbach
Biomechanische Prinzipien
Dieser Technikfehler führt zur Missachtung folgender biomechanischer Prinzipien, welche Einfluss auf die Abwurfgeschwindigkeit nehmen:
- Prinzip des optimalen Beschleunigungsverlaufs und der optimalen Tendenz im Beschleunigungsverlauf:
Nach diesen Prinzipien sollte der Anlauf so gestaltet werden, dass die größten Beschleunigungskräfte erst am Ende erreicht werden, da im der Abwurfposition eine möglichst hohe Endgeschwindigkeit erreicht werden soll. Die Geschwindigkeitstendenz sollte bis zu diesem Zeitpunkt ansteigend sein (Wick, 2013, S.215f).
Findet keine Stemmphase statt, erreicht man diese höchste Geschwindigkeit in der Abwurfposition nicht, da das Stemmbein nicht aktiv gegen den Boden gesetzt wird und somit die Dynamik verloren geht.
Zudem sollte darauf geachtet werden, dass die Geschwindigkeit so zu gestalten ist, dass die Technik nicht darunter leidet. Das bedeutet, dass eine optimale anstatt eine maximale Beschleunigung angestrebt werden sollte, sodass Technikelemente wie der Stemmschritt trotz hoher Geschwindigkeit noch sauber ausgeführt werden können.
- Prinzip der zeitlichen und räumlichen Koordination von Teilimpulsen
Für die Maximierung der Abwurfgeschwindigkeit ist zudem eine zeitlich schnell aufeinanderfolgende und räumlich gleichgerichtete Impulsübertragung wichtig, da die Teilgeschwindigkeiten vektoriell addiert werden (Wick, 2013, S.215f).
Bei dem Überlaufen der Stemmphase gibt es keine optimale Impulsübertragung, da ohne Stemmschritt die erste Stelle der Impulskette gestört wird.
verfasst von Laura Gieser
Zum Abschluss unserer ersten Technikanalyse zeigen wir euch noch Beispiele, welche Weitenauswirkung unterschiedliche Geschwindigkeiten haben.
In unseren vorherigen Beispiel ergaben sich für die Wurfweite des Speer 88,57m bei einer Geschwindigkeit von 30m/s.
Nehmen wir nun an, dass wir einen Speerwerfer haben, der aufgrund des genannten Technikfehlers eine geringere Abwurfgeschwindigkeit von nur 25 m/s erreicht. Bei gleicher Abwurfhöhe und gleichen Abwurfwinkel würde er somit nur auf eine Weite von 62,20m kommen.
Abwurfwinkel
Der Abwurfwinkel Alpha0 ist der Winkel zwischen der Horizontalen und der Tangende an die Schwerpunktbahn des Speers. Dieser ist im obigen Bild bereits eingezeichnet.
Da der Speerwurf eine Freiluft Disziplin ist, die nicht in der Halle ausgeübt werden kann, hat seine Flugbahn auch noch die Einflussgröße des Windes, welcher für den Speer im optimalsten Fall von vorn oder von hinten kommt.
| Tabelle 1: Optimaler Abwurfwinkel (modifiziert nach Killing, 2011, S. 23). | |||
| Speerwurf | Normalbedingung | Gegenwind | Rückenwind |
|---|---|---|---|
| Winkel | 37 - 38 | 34 - 37° | 38 - 41° |
Wir befassen uns erneut mit einem Fehler in der Ausführung und betrachten hierbei folgendes Bild
Das Handgelenk wird fehlerhaft abgeknickt und der Speer wird somit zu steil „angestellt“ (Killing, 2011, S.157). Die Differenz zwischen der roten und der grünen, richtigen, Linie verdeutlicht das Abknicken/Abklappen des Handgelenks. Dies hat zur Auswirkung, dass die Flugkurve verzerrt wird. Der Speer erhält eine steile Flugkurve zu Beginn, fällt jedoch auch wieder schnell steil ab.
Betrachten wir nochmal die Weitenformel und stellen wir uns vor, wir wählen den Extremfall mit dem Abwurfwinkel von 90°, so würde der Speer bei 0 Metern landen. Dies lässt sich durch den Cosinus erklären, denn dieser ist bei 90° 0.
Da wir das Abknicken des Handgelenks betrachtet haben und 90° in diesem Fall eher unrealistisch sind, betrachten wir nun einen Abwurfwinkel von 60° und stellen diesen dem optimalen Winkel gegenüber.
Beispiele:
Angenommen der Winkel ist zu groß gewählt und beträgt 60°, die Abwurfgeschwindigkeit beträgt wieder 30m/s und die anderen Werte übernehmen wir aus den vorherigen Beispielen.
Somit ergibt sich eine Weite W=80,42m
Wählen wir nun den Abwurfwinkel bei optimalen 35° und halten die anderen Werte konstant, so ergibt sich eine Weite von W=88,57
Mit dieser Analyse der Wurftechnik möchten wir zeigen, dass der Speerwurf einen hohen technischen Anspruch besitzt. Jede mögliche Kleinigkeit, wie das Abknicken des Handgelenks, erhält großen Ausschlag auf die Weite. Deshalb ist der Speerwurf eine der anspruchsfolsten Techniken, die es in der Leichtathletik gibt.
verfasst von Sebastian Trittenbach
Flugmechanik
Um diesen Abschnitt möglichst verständlich zu halten, werden nur Kräfte in zwei Dimensionen betrachtet. Wir reduzieren die Beschreibungen auf die Ebene der seitlichen Ansicht, entsprechend der verwendeten Darstellungen. Ebenfalls wird deshalb auf Vektorrechnung verzichtet.
In diesem Kapitel wollen wir, ausgehend von der Weitenformel des schrägen Wurfs, die Größen vorstellen, die einen Einfluss auf den Speer im Flug haben. Bisher wurden schon folgende Größen behandelt:
- Abwurfgeschwindigkeit
- Abwurfwinkel
Die Weitenformel wie sie in WP1203 Kugelstoßen vorgestellt wurde, ist eine direkte Ableitung aus der Formel der Wurfparabel für den Sonderfall $ s_y = 0 $ (Bodenkontakt). Diese Formel beschreibt den schrägen Wurf im luftleeren Raum und berücksichtigt als einzige externe Kraft die Schwerkraft. Beim Kugelstoßen kann argumentiert werden, dass der Luftwiderstand und der Einfluss von Wind, bedingt durch die große Masse, vernachlässigbar sind. Beim Speerwurf ist das dagegen nicht der Fall, denn der Speer besitzt eine geringere Masse bei gleichzeitig größerer Angriffsfläche. Zudem ist seine Flugzeit länger.
Luftwiderstand

Während des Fluges erfährt der Speer, neben der Schwerkraft, auch Widerstandskräfte durch die Luftmoleküle, die ihn umströmen. Wie in DYN6 Reibung erklärt, muss zwischen Flächenwiderstand und Formwiderstand (auch Druckwiderstand genannt) unterschieden werden. Für den Fall, dass der Speer in Richtung seiner Flugbahn zeigt, ist der Formwiderstand zu vernachlässigen, wie Abbildung 8 in der untersten Spalte zeigt. Durch seine spitzen Enden und die dünne Form bietet der Speer kaum Angriffsfläche in Flugrichtung und teilt die Luft ohne Turbulenzen zu erzeugen. Allerdings erzeugt die so entstehende laminare Strömung entlang des Speerkörpers einen Reibungswiderstand durch die Luftmoleküle, die an der Speeroberfläche entlang strömen.
Für den Fall, dass der Speer zur Flugrichtung geneigt ist, ergeben sich Strömungsmuster und Widerstandsverteilungen ähnlich zu Spalte 3 und 4 der Tabelle in Abbildung 8. Für diesen Fall ist der Begriff des Anstellwinkels wichtig. Der Winkel zwischen der Horizontalen und der Speerspitze wird als Anstellwinkel bezeichnet. Die Differenz zwischen der Flugrichtung des Speers und dem Anstellwinkel wird als Angriffswinkel bezeichnet (siehe DYN7 Auftrieb & Strömung). Je größer der Angriffswinkel, desto größer ist der Druckwiderstand auf die Angriffsfläche des Speers.
Zur Verdeutlichung: Die Angriffsfläche für Druckwiderstand entspricht der Fläche, die man sehen kann, wenn man den Speer aus der Richtung betrachtet, in die er fliegt. Der dargestellte Körper in der Tabelle ist ein Querschnitt entlang der Flugrichtung von oben betrachtet. Dieser entsteht, wenn man den Speer parallel zur Flugrichtung in Scheiben schneidet.
Wieso ist dann beim Speerwurf ein größerer Anstellwinkel erwünscht, obwohl er zu höherem Druckwiderstand führt?
Die Antwort liegt in der Aerodynamik. Durch die Anströmung des Speers entsteht auf der Angriffsfläche Druck. Das heißt die Luftmoleküle stauen sich, um an dem Speer vorbeizukommen. Ähnlich wie bei einer Autobahnbaustelle staut es sich, wenn sich die Spuren verengen. Hinter der Baustelle ist die Autobahn dann leer und man hat freie Fahrt. Ähnlich entsteht auf der Rückseite des Speers, durch die geringere Anzahl von Luftteilchen, ein Unterdruck. Dieses Phänomen, welches auch dafür verantwortlich ist, dass Flugzeuge fliegen, wird dynamischer Auftrieb genannt. Man kann also sagen der Speer segelt.
Nach dem Superpositionsgesetz können die so entstehenden Kräfte zum besseren Verständnis aufgeteilt werden, in eine Komponente die in Flugrichtung gerichtet ist und einen Anteil senkrecht zur Flugrichtung. Die Kraft in Flugrichtung ist negativ und bremst den Speer ab. Die Kraft senkrecht zur Flugrichtung verleiht dem Speer Auftrieb so lange die Speerspitze sich über der Flugbahn befindet.
Drehmoment
Um zu erklären, wieso der Speer sich während des Fluges dreht, muss man zwischen Massenmittelpunkt und geometrischem Schwerpunkt unterscheiden (siehe DYN5 Mehrkörpersysteme). Für die Berechnung des geometrischen Schwerpunkts wird angenommen, dass jedes Teil des Speers gleich schwer ist. Somit hat nur die Form des Speers Einfluss auf die Lage des Schwerpunkts. Allerdings ist der Speer aus unterschiedlichen Materialien gefertigt, wodurch sich die Masse ungleichmäßig verteilt. Bei der Berechnung des Massemittelpunkts werden diese Unterschiede mit eingerechnet.
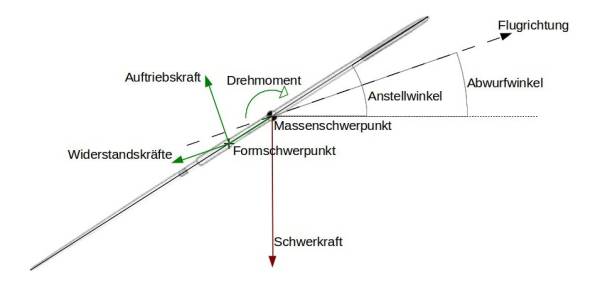
Die IAAF (International Association of Athletics Federations) legt in ihrem Regelwerk den Bereich des Schwerpunkts exakt fest. Er darf, bei einer Speerlänge von 2,6m bis 2,7m, maximal 1,06 m von der Speerspitze entfernt sein. Abbildungen 9 zeigt die unterschiedlichen Schwerpunkte und deren Abstand maßstabsgetreu. Eine vereinfachte Detailansicht zur Entstehung des Drehmoments ist in Abbildung 10 zu sehen.
Zur Erinnerung, es gilt: Je größer der Hebelarm, desto größer das Drehmoment bei gleicher Kraft (siehe DYN4 Rotation). Die Gewichtskraft, als Produkt von Gravitation und Masse, greift am Massenschwerpunkt an und erzeugt somit kein Drehmoment (rot dargestellt). Aus der Schwerkraft resultiert lediglich eine Beschleunigung des gesamten Speers nach unten. Die Widerstands- und Auftriebskräfte hingegen wirken an der Oberfläche des Speers und greifen am Formschwerpunkt an. Der Betrag des Drehmoments berechnet sich aus dem Betrag der Kräfte multipliziert mit dem Hebel senkrecht zur jeweiligen Kraft. Das Gesamtdrehmoment ist die Summe aus den Drehmomenten verursacht durch die Widerstandskräfte und die Auftriebskraft. Wie in DYN4 Rotation beschrieben, wirkt das Drehmoment eines Körpers immer um dessen Massenschwerpunkt.
Während des Fluges kann man drei Phasen unterscheiden.
- In der ersten Phase hat der Speer einen positiven Anstellwinkel. Er erfährt Auftrieb und alle Kräfte erzeugen ein negatives Drehmoment (im Uhrzeigersinn), das den Anstellwinkel verringert (siehe Abbildung 10).
- Wenn die Speerspitze genau in Richtung der Flugbahn zeigt, sind Anstellwinkel und Winkel der Flugbahn gleich groß. Die Angriffsfläche ist vernachlässigbar klein. Es entsteht kein Drehmoment.
- In der letzten Phase ist die Speerspitze tiefer als die Flugbahn des Speers. In diesem Fall wirkt der dynamische Auftrieb nach unten (Abtrieb). Allerdings ist der Angriffswinkel so gering, dass die entstehende Abtriebskraft sehr klein ist. Wie in Abbildung 8 in der letzten Spalte dargestellt, ist der Effekt des Reibungswiderstands wesentlich größer. In dieser Situation erzeugt die Abtriebskraft ein negatives Drehmoment, welches das positives Drehmoment durch die Reibungskräfte kaum verringert.
Ein interessantes Phänomen ist, dass der Reibungswiderstand des Speers stabilisierend wirkt. Die Reibungswiderstandskräfte wirken immer parallel zur Flugbahn. Durch die Lage der Schwerpunkte ergibt sich der zugehörige Hebel $(h_W)$ so, dass sich der Speer immer mit der Spitze in Flugrichtung dreht. Lässt man den Speer aus großer Höhe in beliebiger Ausrichtung fallen, so wird er sich mit der Spitze nach unten ausrichten. Man spricht von einem stabilen System (ähnlich eines Pendels). Dieses mechanische Prinzip ist der Grund, wieso die neueren Speere zuverlässig mit abgesenkter Spitze landen (siehe Abbildung 2).
Exkurs
Für interessierte Leser fassen wir die bisher beschriebenen Größen nun in einer Modellierung des Speerflugs zusammen.Zur Berechnung der Geschwindigkeitsänderung des Speers wird Numerische Integration verwendet. Wissen über dieses Verfahren wird vorrausgesetzt.
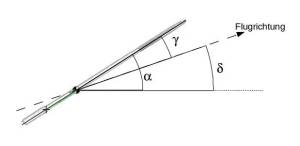
Im Folgenden verwenden wir griechische Buchstaben als Winkelbezeichnung. Der Winkel $\delta$ entspricht zum Zeitpunkt des Abwurfs dem Abwurfwinkel, später stellt es den Winkel zwischen dem Geschwindigkeitsvektor und der Horizontalen dar. Beim Flug des Speers verändert sich dieser Winkel in jedem Zeitschritt. Die Differenz zwischen dem Anstellwinkel $\alpha$ und $\delta$ entspricht dem Angriffswinkel $\gamma$.
Im Gegensatz zum schrägen Wurf kann die Flugbahn nicht mit einer Formel dargestellt werden. Der Luftwiderstand ist abhängig von der Geschwindigkeit des Speers $v$ und dessen Anstellwinkel $\alpha$. Daraus folgt, dass für jeden Zeitschritt, ausgehend vom Abwurf, eine Berechnung der Beschleunigungen $a$ ausgeführt werden muss. Dieses Vorgehen wird Vorwärtssimulation genannt. Je kleiner der Zeitschritt $\Delta{t}$ gewählt wird, desto genauer entspricht die berechnete Annäherung dem exakten Ergebnis.
Die folgenden Gleichungen zeigen den Rechenweg von einer gegebenen Kraft $F$ zur resultierenden Wegstrecke $s$ des Massemittelpunkts für einen Zeitschritt. Diese Formeln sind allgemeingültig und könnten auch zur Berechnung der Flugbahn beim Kugelstoßen verwendet werden. Es wird das Verfahren der numerischen Integration angewendet, was es ermöglicht diese Berechnung direkt auf einem Computer auszuführen. Man kann die Berechnung in eine horizontale (Index $y$) und vertikale Komponente (Index $x$) aufteilen. Die $x$-Achse zeigt in die Gegenrichtung der Gravitation. Die $y$-Achse liegt auf der Erdoberfläche und zeigt vom Abwurfpunkt zum Landepunkt.
;#; <latex>\begin{align*} a_{x_{t}} &= \frac{F_{x_{t}}}{m} & a_{y_{t}} &= \frac{F_{y_{t}}}{m} \\ v_{x_{t+1}} &= a_{x_{t}} * \Delta{t} + v_{x_{t}} & v_{y_{t+1}} &= a_{y_{t}} * \Delta{t} + v_{y_{t}} \\ s_{x_{t+1}} &= v_{x_{t+1}} * \Delta{t} + s_{x_{t}} & s_{y_{t+1}} &= v_{y_{t+1}} * \Delta{t} + s_{y_{t}} \end{align*}</latex> ;#;
Für eine bekannte Kraft $F_t$ kann die resultierende Beschleunigung $a_t$ für den Zeitpunkt $t$ berechnet werden. Das Ergebnis wird in Zeile 2 eingesetzt und ergibt die Geschwindigkeit $v_t$ des Massenschwerpunkts. Eingesetzt in Zeile 3 erhält man die zurückgelegte Wegstrecke $s_t$. Eine so berechnete Reihe $(s_0, s_1, s_2, s_3, s_4,\ldots)$ ergibt die Flugbahn des Speers. Die Kräfte $F_{x_t}$ und $F_{y_t}$ sind die horizontalen und vertikalen Komponenten der resultierenden Kraft $F_R = F_{FW} + F_{RW} + F_{DA} + F_G$ (siehe Abbildung 10) zum Zeitpunkt $t$, mit
<latex>\begin{align*} F_{FW_t} = A_{A_t} * c_{W_t} * \frac{\rho}{2} * v_t^2 \ \ \ \ \end{align*}</latex> Formwiderstand
<latex>\begin{align*} F_{RW_t} = \eta \frac{\Delta{v_t}}{\Delta{\rho}}A_O \ \ \ \ \end{align*}</latex> Reibungswiderstand
<latex>\begin{align*} F_{DA_t} = A_{A_t} * c_{A_t} * \frac{\rho}{2} * v_t^2 \ \ \ \ \end{align*}</latex> dynamischer Auftrieb
<latex>\begin{align*} F_G = m * g \ \ \ \ \end{align*}</latex> Gewichtskraft
$A_A$ ist die Angriffsfläche des Speers und hängt von dem Angriffswinkel $\gamma$ ab.
$c_W$ beschreibt den Widerstandsbeiwert, eine Materialeigenschaft der Speeroberfläche, abhängig von $\gamma$.
$\rho$ repräsentiert die Dichte von Luft.
$A_O$ stellt die Oberfläche des Speers dar.
$\Delta{v}$ ist der Geschwindigkeitsunterschied zwischen Speer und Luft.
$\Delta{\rho}$ Differenz der Dichte zwischen Speer und Luft.
$c_A$ repräsentiert den Auftriebskoeffizent, eine Materialeigenschaft des Speers, in Abhängigkeit von $\gamma$.
Anhand Abbildung 9 kann man die horizontale und vertikale Komponente wie folgt herleiten: ;#; <latex>\begin{align*} F_{x_t} &= (F_{FW_t} + F_{RW_t})*cos(\delta_t) + F_{DA_t}*sin(\delta_t)\\ F_{y_t} &= (F_{FW_t} + F_{RW_t})*sin(\delta_t) + F_{DA_t}*cos(\delta_t) - F_G \end{align*}</latex> ;#;
Die so berechneten Kräfte werden im nächsten Zeitschritt benötigt für die Berechnung der Beschleunigung $a$.
Wie bereits erwähnt, erzeugen die Kräfte nicht nur lineare Beschleunigung, sondern auch ein Drehmoment um den Massenschwerpunkt des Speers. Nach Abbildung 10 ergibt sich die Formel für das Drehmoment zu ;#; <latex>\begin{align*} M_t = ((F_{FW_t} + F_{RW_t})*h_{W_t}) +(F_{DA_t}*h_{DA_t}). \end{align*}</latex> ;#;
Nach dem Stufenwinkelsatz ist $h_{W_t} = h*cos(\gamma_t)$ und $h_{DA_t} = h*sin(\gamma_t)$, wobei $h$ dem Abstand zwischen Formschwerpunkt und Massenschwerpunkt entspricht. Es fällt auf, dass für einen kleinen Angriffswinkel der Hebel für die Auftriebskraft sehr klein wird, wohingegen der Hebel des Reibungswiderstandes maximal wird.
Ähnlich wie aus den wirkenden Kräften Beschleunigungen resultieren, so erzeugt das Drehmoment eine Wikelbeschleunigung. Wir schreiben die resultierende Winkelgeschwindigkeit direkt in Abhängigkeit des Drehmoments, als
;#; <latex>\begin{align*} \omega_{t+1} = \frac{M_t * \Delta{t}}{I} + \omega_t \end{align*}</latex> ;#;
Das Trägheitsmoment $I$ ist eine Materialeigenschaft des Speers und beschreibt wie stark sich ein Drehimpuls auf die Winkelgeschwindigkeit auswirkt. Je schwerer das Objekt und je größer der Abstand der Massen vom Drehzentrum, desto größer ist das Trägheitsmoment.
Bei gegebener Winkelgeschwindigkeit $\omega$ kann der Anstellwinkel für den nächsten Zeitschritt wie folgt berechnet werden. ;#; <latex>\begin{align*} \alpha_{t+1} = \omega_{t+1} * \Delta{t} + \alpha_t \end{align*}</latex> ;#;
Der Winkel $\delta_t$ ist zu Beginn gegeben und ergibt sich während der Simulation aus dem Verhältnis von $(s_{y_t}-s_{y_{t-1}})$ zu $(s_{x_t}-s_{x_{t-1}})$.
Somit sind alle Größen bestimmt, um die Simulation im nächsten Zeitschritt zu berechnen. Man beginnt die Fläche $A_{A_t}$ und die Geschwindigkeitsdifferenz $\Delta{v_t}$ zu berechnen. Danach kann man die resultierenden Kräfte berechnen und mit Hilfe deren die Beschleunigung des Speers.
verfasst von Florian Kunz
Ausblick
Wie in diesem Wiki deutlich wird, ist der Speerwurf eine sehr anspruchsvolle Disziplin in der Leichtathletik.
Im Bereich der Wurftechnik kann man noch sehr viel erarbeiten und mögliche weitere Wikis erstellen.
Hierbei kann es sich um weitere Technikfehler handelt.
Beispiele hierführ wären:
- Impulsschritt hintenherum
- Arm zu weit unten beim Abwurf
- gebeugter Wurfarm
Viele Fehlerbilder finden sie unter folgendem Link:
http://www.speerschule.ch/xanalysonicht.htm
Doch es gibt auch positiv Bilder, die man genauer untersuchen kann, so ist der Speerwurf mittlerweile kein gradliniger Wurf, sondern bei der Abwurfbeschleunigung wird auch eine Rotation ausgeübt.
Schönes Beispiel hierfür:
http://www.speerschule.ch/vids/archiv/dezordo2011.mov
verfasst von Sebastian Trittenbach
Im Bereich der Flugmechanik wurde zwar der Luftwiderstand und der Effekt des dynamischen Auftriebs behandelt, allerdings wurden damit nur grundlegend die Größen behandelt, welche den Flug beeinflussen. Man könnte das Thema erweitern um:
- Schwingung des Speers
- Rotation um die Längsachse
- Drehmomente um die Hochachse
- Modellierung von Gegen- oder Rückenwind
- Aerodynamische Effekte durch Seitenwind
Bei Interesse kann man sich mit diesem Simulator die Flugbahn für beliebige Anfangswerte berechnen. Wie gut das Modell ist, auf dem das Programm basiert, konnten wir nicht feststellen. Die Ergebnisse für verschiedene Abwurfwinkel und Angriffswinkel lassen jedoch vermuten, dass es sich um ein lineares Modell handelt, welches nicht besonders ausgereift ist. Hier könnte man basierend auf diesem Artikel ein exakteres Modell entwickeln.
Auch ein Mess-Projekt wäre denkbar, bei dem Abwurfgeschwindigkeit, Abwurf- und Anstellwinkel ermittelt werden sowie die resultierende Wurfweite.
verfasst von Florian Kunz
Fragen
<spoiler |1. Ist eine maximale Anlaufgeschwindigkeit für die Technik und somit auch die Wurfweite optimal?>
Nein. Bei einer maximalen Anlaufgeschwindigkeit ist es zwar in der Theorie die beste Voraussetzung für den weitesten Wurf, doch ist es schwer, bis unmöglich, das Prinzip der zeitlichen und räumlichen Koordination von Teilimpulsen zu erfüllen. Ebenso schwierig wird der Stemmschritt. Es ist vergleichbar mit dem plötzlichen Stoppen bei einem Sprint. Ein Fehler wie das Überlaufen wird dadurch ebenso provoziert.
</spoiler>
<spoiler |2. Wie kann man die Wurfweite optimieren, indem man den Winkel verändert?>
Man passt den Winkel dem Optimum an, indem man den Abwurfwinkel und den Anstellwinkel anpasst.
Ebenso muss man den Winkel an die äußeren Bedingungen anpassen. Hierbei sind Gegenwind und Rückenwind gemeint.
</spoiler>
<spoiler |3. Wie entsteht das Drehmoment beziehungsweise Kippmoment?>
Die Kräfte durch Luftwiderstand und dynamischen Auftrieb greifen am Formschwerpunkt an und haben somit einen Hebel zum Massenschwerpunkt. Dies erzeugt ein Drehmoment.
</spoiler>
Quellen
Literatur
01: Ballreich, R. & Baumann, W. (1986). Biomechanik der Sportarten - Band 1: Biomechanik der Leichtathletik. Stuttgart: Enke.
02: Haberkorn, C. & Plaß, R. (1992). Spezielle Didaktik der Sportarten - Leichtathletik 2 - Sprung Wurf Stoß. Frankfurt(a.M.): Diesterweg.
03: Hinz, L. (1991). Leichtathletik Wurf und Stoß - Analysen und Empfehlungen für die Disziplinen Kugelstoßen, Diskuswerfen, Speerwerfen und Hammerwerfen. Berlin: Sportverlag Berlin.
04: Kassat, G. (1993). Biomechanik für Nicht-Biomechaniker : alltägliche bewegungstechnisch-sportpraktische Aspekte. Bünde: Fitness-Contur-Verlag.
05: Killing, W. (2011). Jugendleichtathletik : offizieller Rahmentrainingsplan des Deutschen Leichtathletik-Verbandes für die Wurfdisziplinen im Aufbautraining. Münster : Philippka-Sportverl.
06: Wick, D. (2013). Biomechanik im Sport : Lehrbuch der biomechanischen Grundlagen sportlicher Bewegung . Balingen : Spitta-Verlag.
07: Willimczik, K. (1989). Biomechanik der Sportarten: Grundlagen, Methoden, Analysen. Reinbek bei Hamburg : Rowohlt.
Internetquellen
08: Campos, J. & Brizuela, G. & Ramón, V. (2004) Three-dimensional kinematic analysis of elite javelin throwers at the 1999 IAAF World Championships in Athletics. Zugriff am 04. Februar 2014 unter http://www.worldofjavelin.com/wp-content/uploads/2010/11/Three-dimensional-kinematic-analysis-of-elite-javelin-throwers-at-the-1999-IAAF-World-Championships-in-Athletics-NSA-2004.pdf.
09: Fuchser, I. Kleine Speerkunde. Zugriff am 04. Februar 2014 unter http://www.speerschule.ch/xdownspeer.htm.
10: Hatton, L. (2011) Publication Page. Zugriff am 04. Februar 2014 unter http://www.leshatton.org/javelin_2005.html.
11: IAAF (2013) Competition Rules 2014-2015. Zugriff am 04. Februar 2014 unter http://www.iaaf.org/download/download?filename=a3588664-5eff-49c2-977a-4665a12c19bf.pdf&urlslug=IAAF%20Competition%20Rules%202014-2015.
12: Institut für Motorik und Bewegungstechnik, Deutsche Sporthochschule Köln. Der Speerwurf. Zugriff am 04.04.2014 unter http://www.dshs-koeln.de/imb/Individualsport/content/e40/e10480/e10515/e10528/e10710/Speer_ger.pdf.
13: Johan (2009) Physics: Wind and Javelin, what’s the verdict?. Zugriff am 04. Februar 2014 unter http://www.worldofjavelin.com/posts/physics-wind-and-javeli-whats-the-verdict/
14: Murakami, M. & Tanabe, S. & Ishikawa, M. & Isolehto, J. & Komi, P. V. & Ito, A. (2006) Biomechanical analysis of the javelin at the 2005 IAAF World Championships in Athletics. Zugriff am 04. Februar 2014 unter http://www.worldofjavelin.com/wp-content/uploads/2010/11/Biomechanical-analysis-of-the-javelin-at-the-2005-IAAF-World-Championships-in-Athletics-NSA-2006.pdf.
15: Ritschel, M. Speerwurf - Methodik von Disziplinen. Zugriff am 04. Februar 2014 unter http://www.leichtathletik.de/index.php?SiteID=832.
16: Röhler, T. (2013). Speerwurf. Zugriff am 04. Februar 2014 unter http://www.thomas-roehler.de/speerwurf/.
17: Schwiek, F. (2013). Technik beim Speerwurf. Zugriff am 04. Februar 2014 unter http://speerwerfen.org/technik-beim-speerwurf/.
Videos
18: hoslat. (2011). IAAF Diamond League 2011 Brussels Speerwurf De Zordo. Zugriff am 04. Februar 2014 unter http://www.youtube.com/watch?feature=player_embedded&v=t6E_644eGDc.
Abbildungen
Modul-Icon: laobc. (2010). Javelin throw silhouette. Zugriff am 04. Februar 2014 unter http://openclipart.org/detail/75955/javelin-throw-silhouette-by-laobc.
Abb. 1: Clarkson, S. (2012). Wurfparabel alt. Zugriff am 04. Februar 2014 unter http://speerschule.ch/pics/parabel-alt.jpg.
Abb. 2: Clarkson, S. (2012). Wurfparabel neu. Zugriff am 04. Februar 2014 unter http://speerschule.ch/pics/parabel-neu.jpg.
Abb. 3: Gieser, L. (2014). Weitenformel.
Abb. 4: Dober, R. (2012). Impulsübertragung Speerwurf. Zugriff am 04. Februar 2014 unter http://sportunterricht.de/lksport/speimpuls.html.
Abb. 5: Trittenbach, S. (2014). Technikfehler Stemmschritt falsch.
Abb. 6: Trittenbach, S. (2014). Technikfehler Stemmschritt richtig.
Abb. 7: Trittenbach, S. (2014). Technikfehler Handgelenk.
Abb. 8: Kunz, F. (2014). Luftströmung um verschiedene Körperquerschnitte.
Abb. 9: Kunz, F. (2014). Skizze Speer im Flug.
Abb.10: Kunz, F. (2014). Entstehung des Drehmoments beim Speer.
Abb.11: Kunz, F. (2014). Darstellung der Winkel beim Speerwurf.
Bewertung des Wiki-Moduls
| Kategorie | Gieser | Trittenbach | Kunz | Anmerkungen |
|---|---|---|---|---|
| Inhalt (max. 10) | 07 Pkt | 06 Pkt | 10 Pkt | mehr Bezüge zu Grundlagenwikis und zu biomechanischen Begriffen benötigt |
| Form (max. 5) | 04 Pkt | 04 Pkt | 04 Pkt | Titel-Hierarchie unstimmig ('Inhalte' weglassen), sprachliche Fehler |
| Bonus (max. 2) | 00 Pkt | 01 Pkt | 02 Pkt | eigene Bilder erstellt, Zusammenhänge durch Formeln unterlegt, Exkurs Modellierung |
| Einzelbewertung | 11 Pkt | 11 Pkt | 16 Pkt | 15 Punkte = 100% |
| Gesamtbewertung | 38/45 Punkte = 84% | |||